Univariate optimization

Introduction to Optimization in Python

Jasmin Ludolf

Content Developer

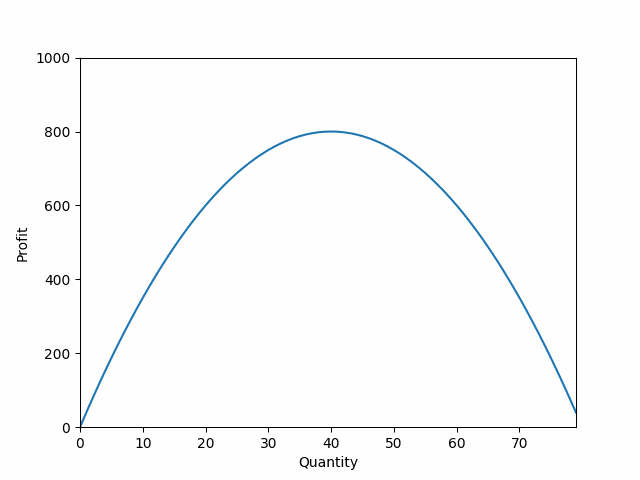
Example: Optimization in manufacturing

 

Objective function:

$P = 40q - 0.5q^2$

  • Univariate: has one variable

Profit varying with quantity.

Introduction to Optimization in Python

Example: Optimization in manufacturing

 

Objective function:

$P = 40q - 0.5q^2$

  • Univariate: has a single variable

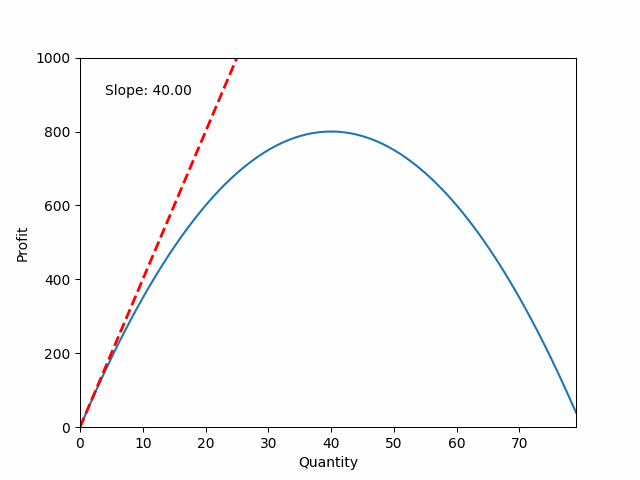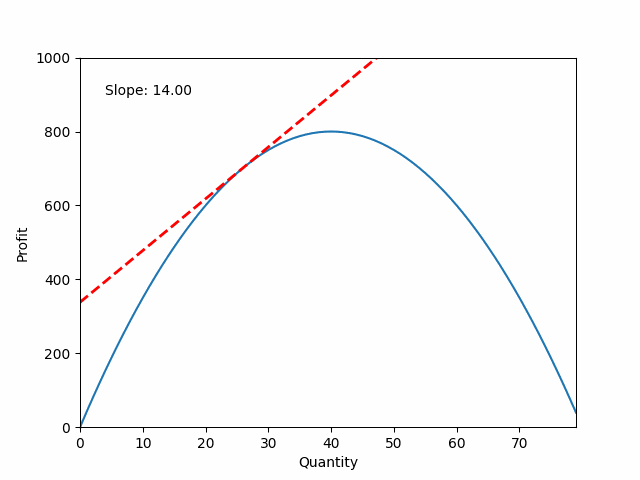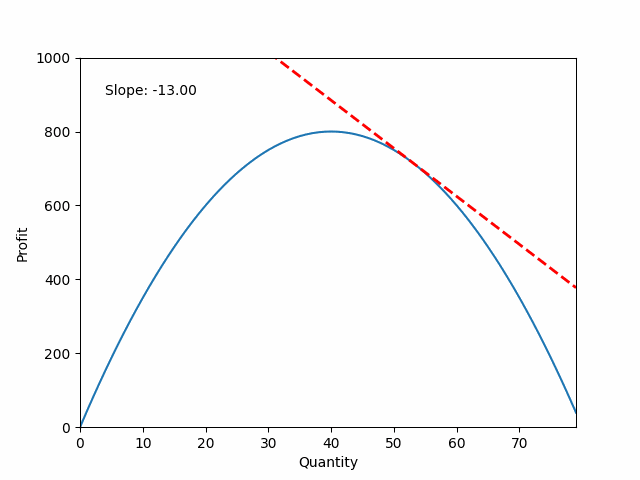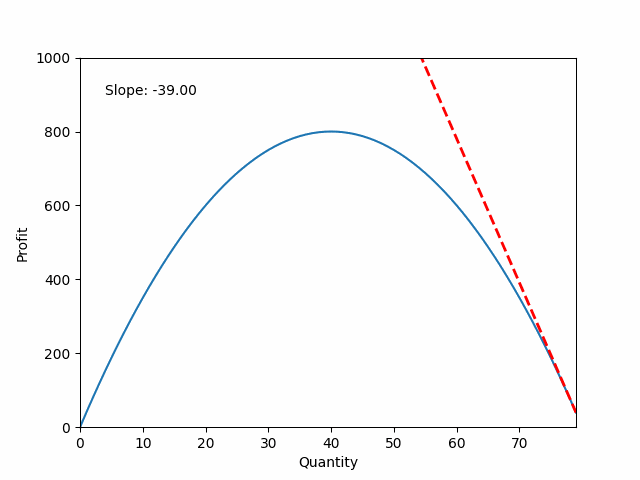
Profit varying with quantity.

Introduction to Optimization in Python

Calculating derivatives

 

Objective function:

$P = 40q - 0.5q^2$

Derivative: describes how the slope behaves

$\frac{dP}{dq} = 40 - q$

from sympy import symbols, diff, solve


q = symbols('q')

P = 40 * q - 0.5 * q**2

dp_dq = diff(P)

print(f"The derivative is: {dp_dq}")

The derivative is: 40 - 1.0*q
1 https://docs.sympy.org/latest/index.html
Introduction to Optimization in Python

The critical point

Optimum is found where the derivative function equals zero

  • Critical points: points where the derivative function is zero

Optimum $q$ satisfies:

$\frac{dP}{dq} = 40 - q = 0$

q_opt = solve(dp_dq)
print(f"Optimum quantity: {q_opt}")

Optimum quantity: [40.0000000000000]
Introduction to Optimization in Python

Maxima, minima, or neither?

 

Profit varying with quantity.

 

Objective function:

$p = 40q - 0.5q^2$

q_opt = solve(p_prime)
print(f"Optimum quantity: {q_opt}")

Optimum quantity: [40.0000000000000]
Introduction to Optimization in Python

Convexity and concavity

 

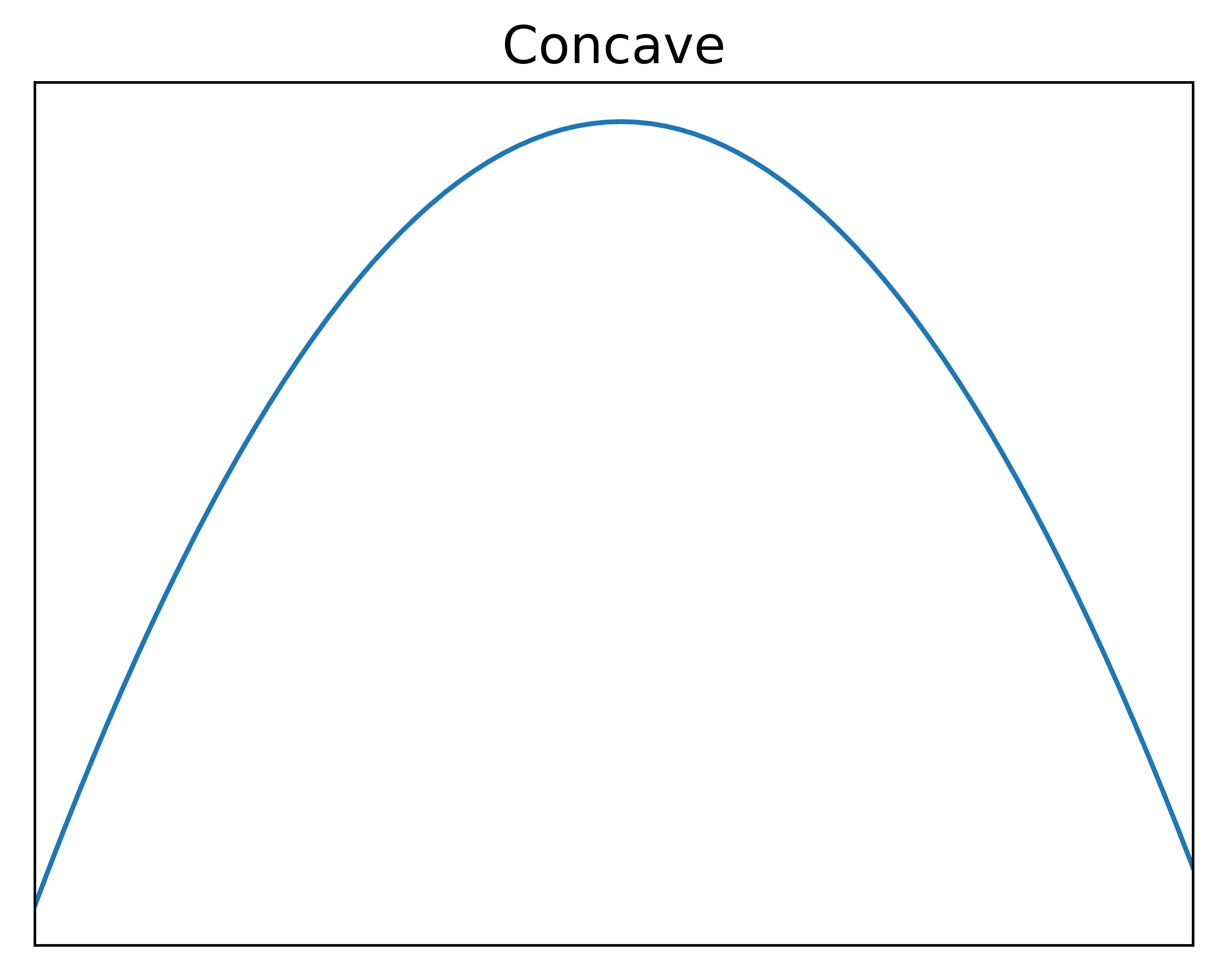
Concave function.

  • Maxima

 

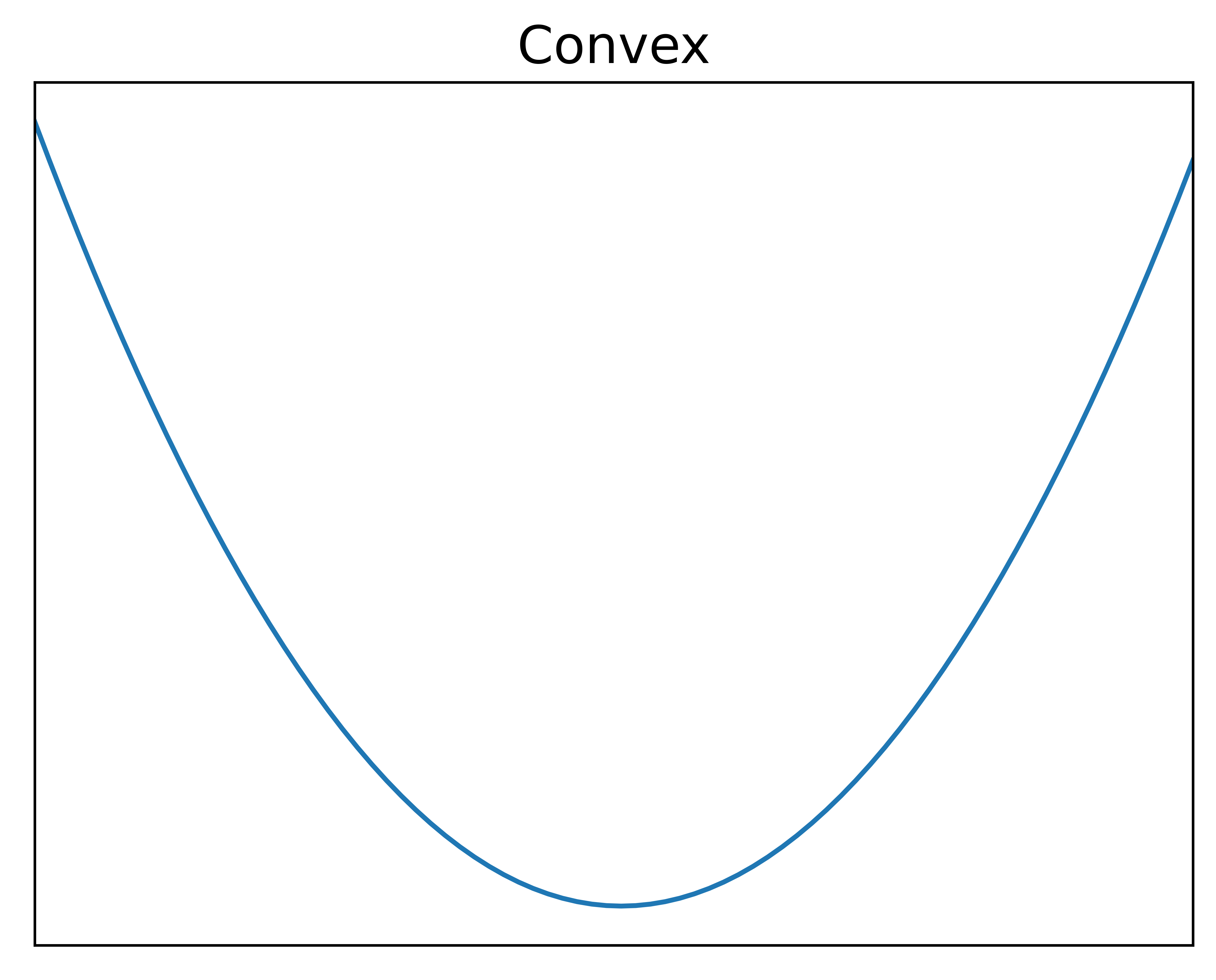
Convex function.

  • Minima
Introduction to Optimization in Python

Second derivative

 

  • The derivative of the derivative
  • Rate the slope changes as the variable changes

 

  • If 2nd derivative at the point $< 0$: Maxima
  • If 2nd derivative at the point $> 0$: Minima
  • If 2nd derivative at point $= 0$: neither

Profit varying with quantity.

Introduction to Optimization in Python

Example: Maximum, minimum, or neither?

 

Derivative:

$\frac{dp}{dq} = 40 - q$

 

Second derivative:

$\frac{d^2p}{dq^2} = -1 < 0$

  • Maxima!

 

d2p_dq2 = diff(dp_dq)

sol = d2p_dq2.subs('q', q_opt)


print(f"The 2nd derivative is: {sol}")

The 2nd derivative is: -1.0000000000000
Introduction to Optimization in Python

Derivatives in optimization

 

  • First derivatives
    • Find critical points in optimization problems
  • Second derivatives
    • Identify as minima or maxima
Introduction to Optimization in Python

Let's practice!

Introduction to Optimization in Python

Preparing Video For Download...