Moving forward when model assumptions are violated
Inference for Linear Regression in R

Jo Hardin
Professor, Pomona College
Linear model
$$\huge{Y = \beta_0 + \beta_1 \cdot X + \epsilon}$$
$$\large{\text{where } \epsilon \sim N(0, \sigma_\epsilon)}$$
Transforming the explanatory variable
$Y = \beta_0 + \beta_1 \cdot X + \beta_2 \cdot X^2 + \epsilon$, where $\epsilon \sim N(0, \sigma_\epsilon)$
$Y = \beta_0 + \beta_1 \cdot \ln(X) + \epsilon$, where $\epsilon \sim N(0, \sigma_\epsilon)$
$Y = \beta_0 + \beta_1 \cdot \sqrt{X} + \epsilon$, where $\epsilon \sim N(0, \sigma_\epsilon)$
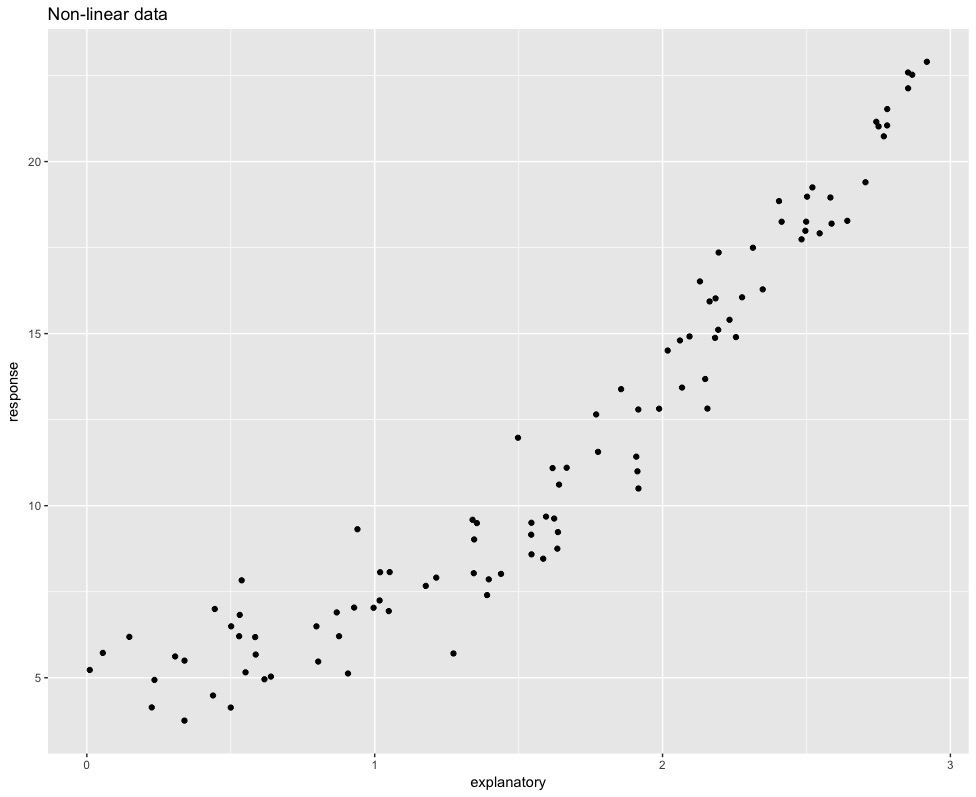
Squaring the explanatory variable
ggplot(data=data_nonlinear,
aes(x=explanatory, y=response)) +
geom_point()
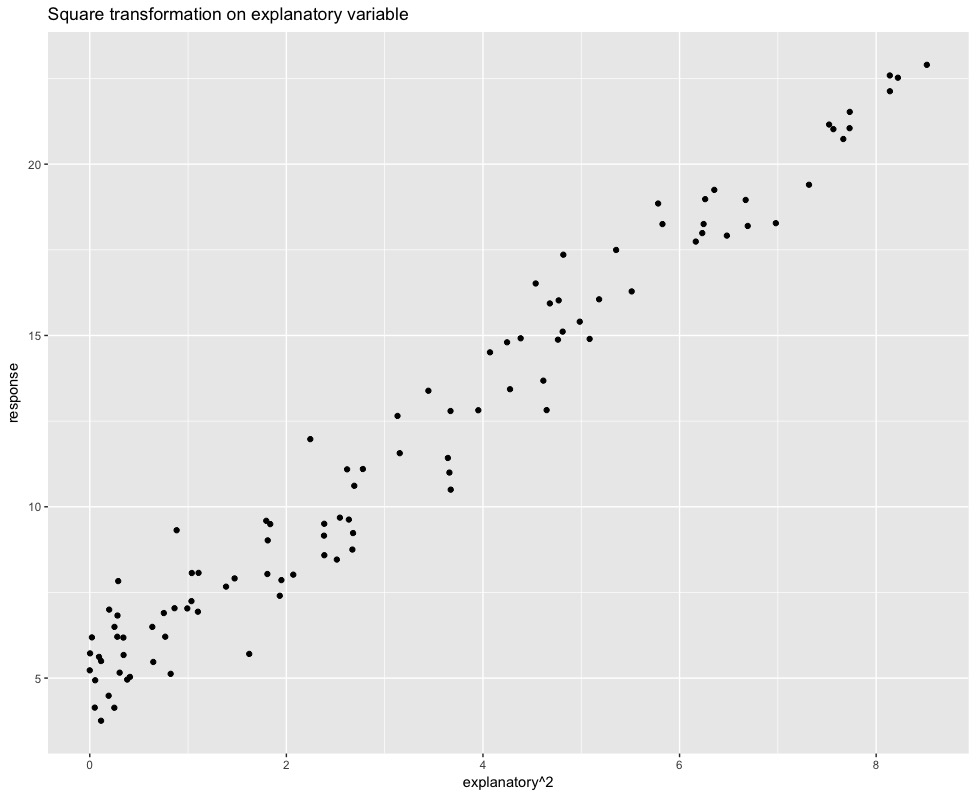
ggplot(data=data_nonlinear,
aes(x=explanatory^2, y=response))+
geom_point()
Transforming the response variable
$Y^2 = \beta_0 + \beta_1 \cdot X + \epsilon$, where $\epsilon \sim N(0, \sigma_\epsilon)$
$\ln(Y) = \beta_0 + \beta_1 \cdot X + \epsilon$, where $\epsilon \sim N(0, \sigma_\epsilon)$
$\sqrt(Y) = \beta_0 + \beta_1 \cdot X + \epsilon$, where $\epsilon \sim N(0, \sigma_\epsilon)$
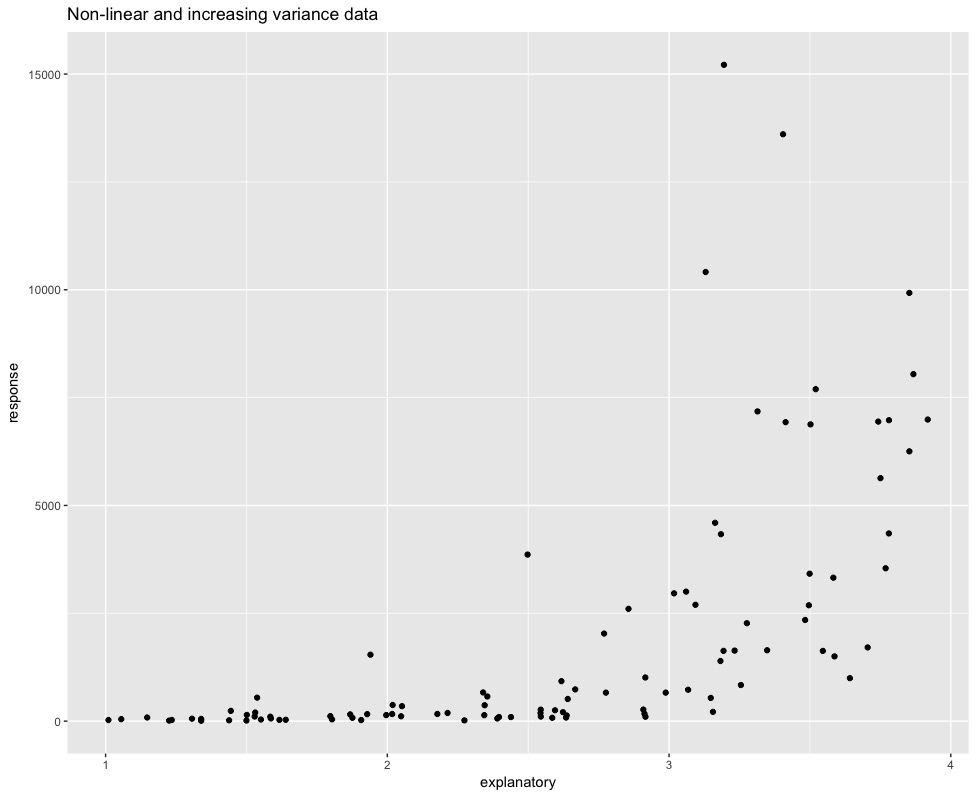
A natural log transformation
ggplot(data = data_nonnorm,
aes(x = explanatory, y = response)) +
geom_point()
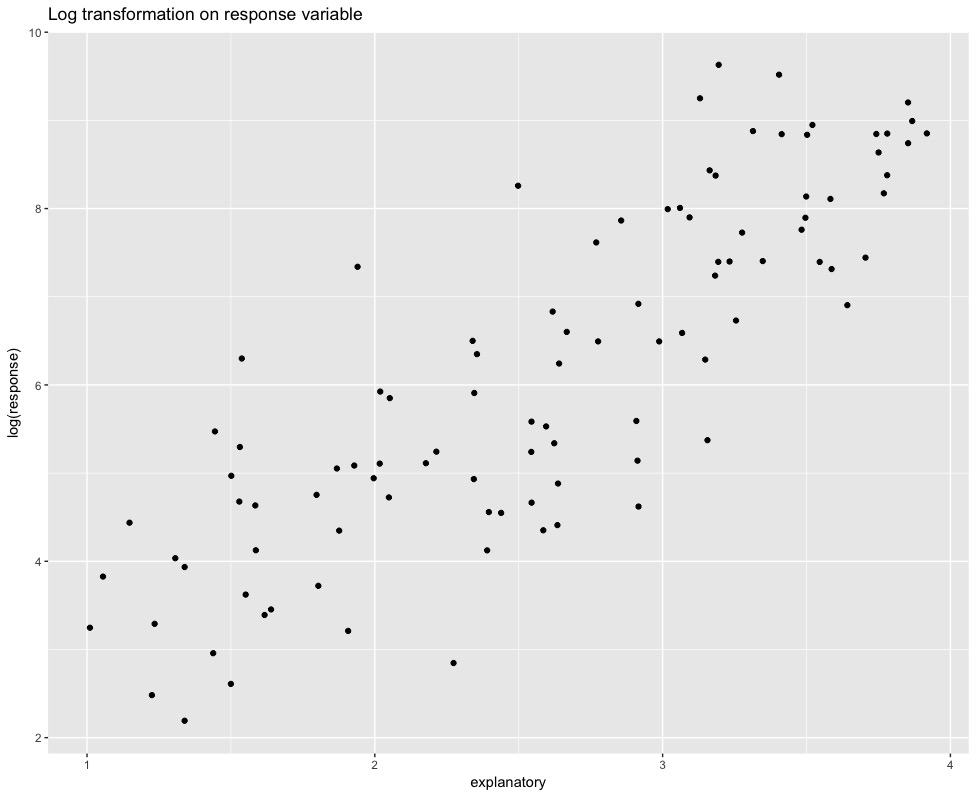
ggplot(data = data_nonnorm,
aes(x = explanatory, y = log(response))) +
geom_point()
Let's practice!
Inference for Linear Regression in R

