Power analysis: sample and effect size

Experimental Design in Python

James Chapman

Curriculum Manager, DataCamp

A primer on effect size

Effect size: Quantifies the difference between two groups

Cohen's d: Standard measure for effect size

Two plants treated with different fertilizers that have grown to different heights. There's an arrow indicating the difference in height to represent the effect size.

The dataset: video game engagement

60 participants
- 30 assigned randomly to Action
- 30 assigned randomly to Puzzle

video_game_data.head()

   Game_Genre  Engagement_Time
0      Action              5.1
1      Puzzle              4.4
2      Action              7.2
3      Action              5.3
4      Puzzle              2.7

Calculating power overview

Power: the probability of correctly rejecting a false null hypothesis: ($1 - \beta$)
- Ranges between 0 and 1 (certainty in ability to detect a true effect)
Assume effect_size=1 from historical data

from statsmodels.stats.power import TTestIndPower
power_analysis = TTestIndPower()

power = power_analysis.solve_power(effect_size=1, nobs1=30, alpha=0.05)
print(power)

0.9677082519951168

Cohen's d formulation

def cohens_d(group1, group2):

    diff = group1.mean() - group2.mean()
    n1, n2 = len(group1), len(group2)
    var1, var2 = group1.var(), group2.var()

    pooled_std = np.sqrt(((n1 - 1) * var1 + (n2 - 1) * var2) / (n1 + n2 - 2))

    d = diff / pooled_std
    return d

Pooled Standard Deviation: $\sigma_{p} = \sqrt{\frac{(n_1 - 1) \times \text{var}_1 + (n_2 - 1) \times \text{var}_2}{n_1 + n_2 - 2}}$

Cohen's d for video game data

action_times = video_game_data[video_game_data['Game_Genre'] == 'Action']['Engagement_Time']
puzzle_times = video_game_data[video_game_data['Game_Genre'] == 'Puzzle']['Engagement_Time']


d = cohens_d(action_times, puzzle_times)

print(f"Cohen's d: {d}")

Cohen's d: 1.161524633221452

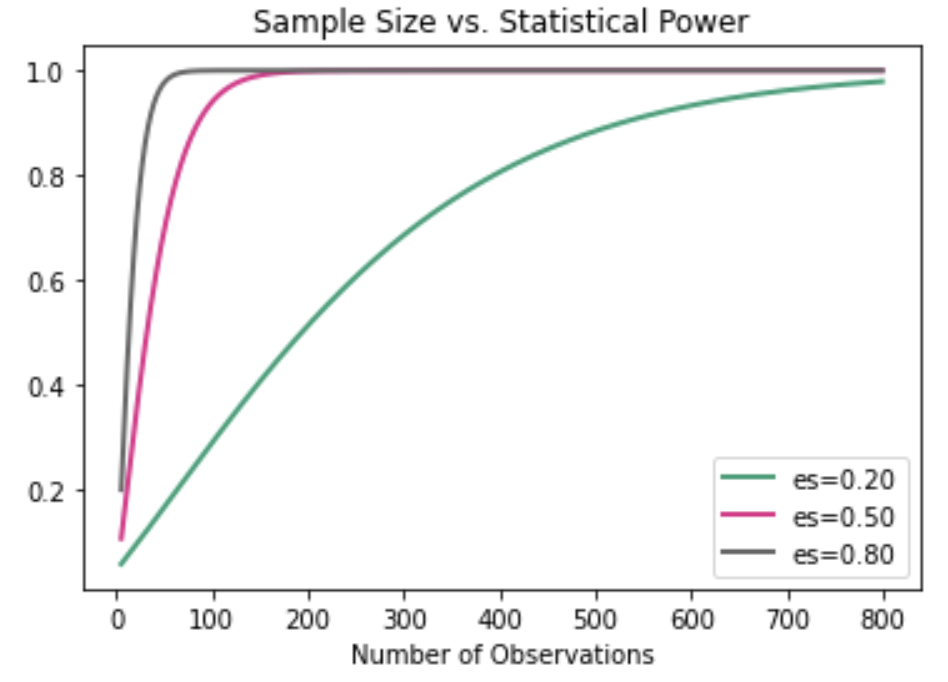
Understanding sample size and power

Trade-off in balancing power and sample size
Larger sample sizes increase study power

Sample size vs. Statistical Power.png

¹ https://grabngoinfo.com/power-analysis-for-sample-size-using-python/

Sample size calculation in context

Response variable: engagement_time

from statsmodels.stats.power import TTestIndPower
power_analysis = TTestIndPower()
required_n = power_analysis.solve_power(effect_size=d, alpha=0.05, 
                                        power=0.99, ratio=1)
print(required_n)

28.237827708942007

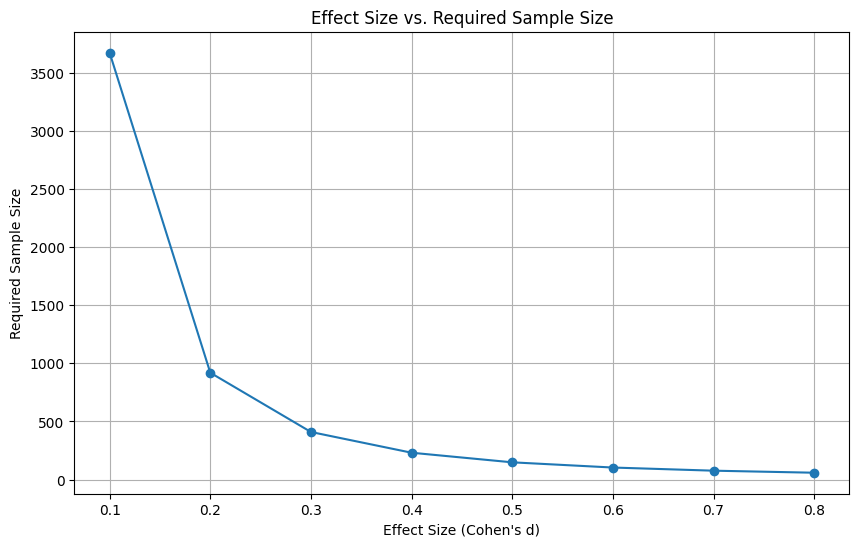
Visualizing sample size requirements

import numpy as np
import matplotlib.pyplot as plt
effect_sizes = np.linspace(0.1, 0.8, 8)
sample_sizes = [power_analysis.solve_power(effect_size=es, alpha=0.05, power=0.99, 
                                           ratio=1) for es in effect_sizes]

plt.figure(figsize=(10, 6))
plt.plot(effect_sizes, sample_sizes, 'o-')
plt.title('Effect Size vs. Required Sample Size')
plt.xlabel('Effect Size (Cohen\'s d)')
plt.ylabel('Required Sample Size')
plt.grid(True)
plt.show()

Visualizing sample size requirements

Effect Size vs. Required Sample Size.png

Let's practice!

Experimental Design in Python