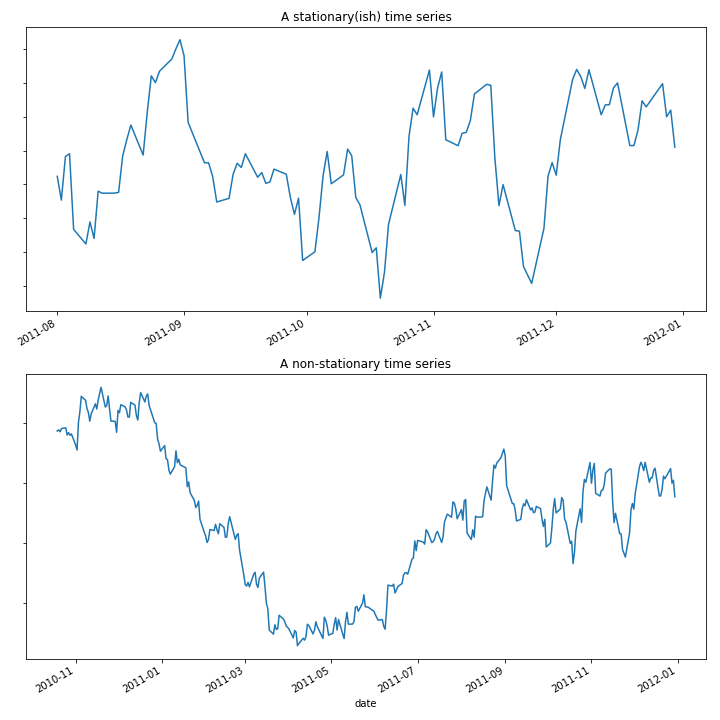
Stationarity and stability

Machine Learning for Time Series Data in Python

Chris Holdgraf

Fellow, Berkeley Institute for Data Science

Stationarity

Stationary time series do not change their statistical properties over time
E.g., mean, standard deviation, trends
Most time series are non-stationary to some extent

Model stability

Non-stationary data results in variability in our model
The statistical properties the model finds may change with the data
In addition, we will be less certain about the correct values of model parameters
How can we quantify this?

Cross validation to quantify parameter stability

One approach: use cross-validation
Calculate model parameters on each iteration
Assess parameter stability across all CV splits

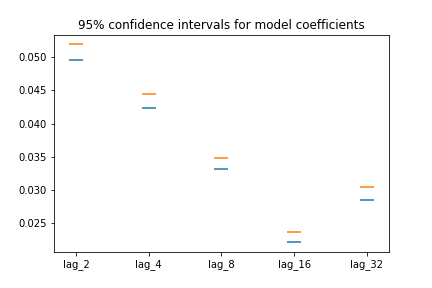
Bootstrapping the mean

Bootstrapping is a common way to assess variability
The bootstrap:
1. Take a random sample of data with replacement
2. Calculate the mean of the sample
3. Repeat this process many times (1000s)
4. Calculate the percentiles of the result (usually 2.5, 97.5)

The result is a 95% confidence interval of the mean of each coefficient.

Bootstrapping the mean

from sklearn.utils import resample

# cv_coefficients has shape (n_cv_folds, n_coefficients)
n_boots = 100
bootstrap_means = np.zeros(n_boots, n_coefficients)
for ii in range(n_boots):
    # Generate random indices for our data with replacement, 
    # then take the sample mean
    random_sample = resample(cv_coefficients)
    bootstrap_means[ii] = random_sample.mean(axis=0)

# Compute the percentiles of choice for the bootstrapped means
percentiles = np.percentile(bootstrap_means, (2.5, 97.5), axis=0)

Plotting the bootstrapped coefficients

fig, ax = plt.subplots()
ax.scatter(many_shifts.columns, percentiles[0], marker='_', s=200)
ax.scatter(many_shifts.columns, percentiles[1], marker='_', s=200)

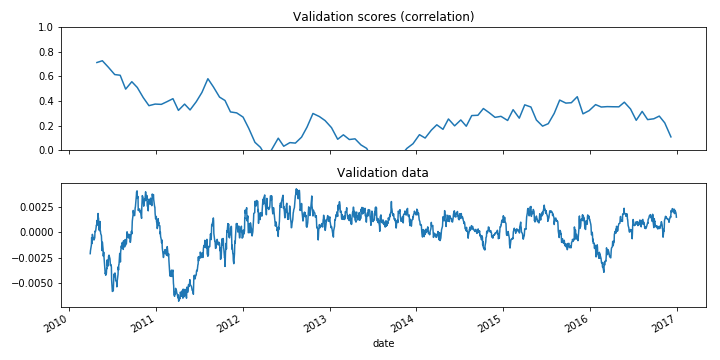
Assessing model performance stability

If using the TimeSeriesSplit, can plot the model's score over time.
This is useful in finding certain regions of time that hurt the score
Also useful to find non-stationary signals

Model performance over time

def my_corrcoef(est, X, y):
    """Return the correlation coefficient 
    between model predictions and a validation set."""
    return np.corrcoef(y, est.predict(X))[1, 0]

# Grab the date of the first index of each validation set
first_indices = [data.index[tt[0]] for tr, tt in cv.split(X, y)]

# Calculate the CV scores and convert to a Pandas Series
cv_scores = cross_val_score(model, X, y, cv=cv, scoring=my_corrcoef)
cv_scores = pd.Series(cv_scores, index=first_indices)

Visualizing model scores as a timeseries

fig, axs = plt.subplots(2, 1, figsize=(10, 5), sharex=True)

# Calculate a rolling mean of scores over time
cv_scores_mean = cv_scores.rolling(10, min_periods=1).mean()
cv_scores.plot(ax=axs[0])
axs[0].set(title='Validation scores (correlation)', ylim=[0, 1])

# Plot the raw data
data.plot(ax=axs[1])
axs[1].set(title='Validation data')

Visualizing model scores

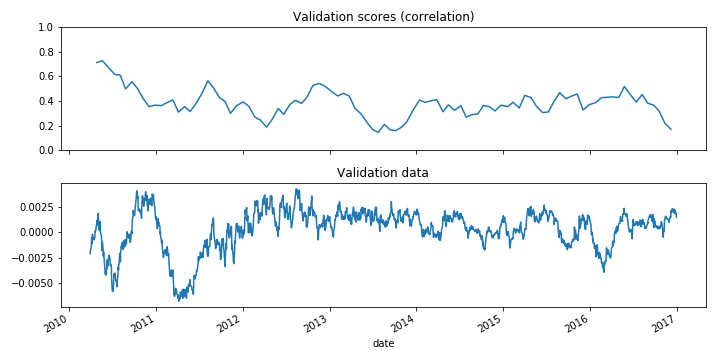
Fixed windows with time series cross-validation

# Only keep the last 100 datapoints in the training data
window = 100

# Initialize the CV with this window size
cv = TimeSeriesSplit(n_splits=10, max_train_size=window)

Non-stationary signals

Let's practice!

Machine Learning for Time Series Data in Python