Regularization

Machine Learning with PySpark

Andrew Collier

Data Scientist, Fathom Data

Features: Only a few

Dataset with a few features

Features: Too many

Dataset with many features

Features: Selected

Selecting features from a dataset with many features

Loss function (revisited)

Linear regression aims to minimise the MSE.

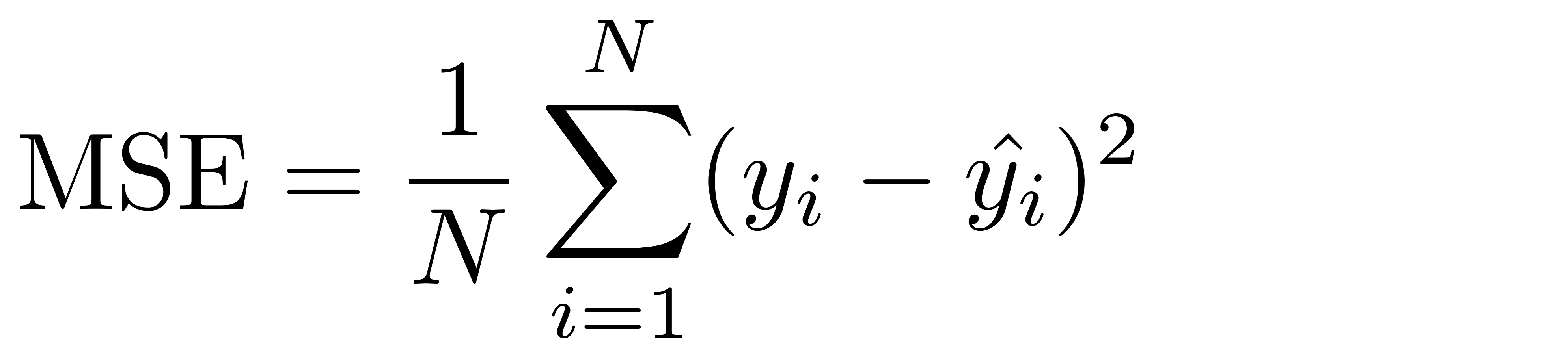
Mean Square Error loss function

Loss function with regularization

Linear regression aims to minimise the MSE.

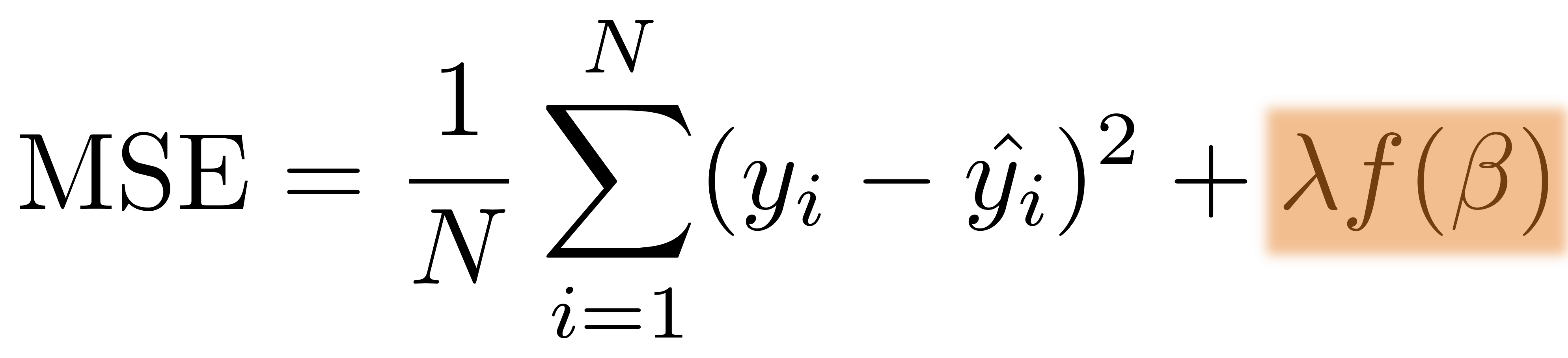
Mean Square Error loss function with regularization term

Add a regularization term which depends on coefficients.

Regularization term

An extra regularization term is added to the loss function.

The regularization term can be either

Lasso — absolute value of the coefficients
Ridge — square of the coefficients

It's also possible to have a blend of Lasso and Ridge regression.

Strength of regularization determined by parameter $\lambda$:

$\lambda = 0$ — no regularization (standard regression)
$\lambda = \infty$ — complete regularization (all coefficients zero)

Cars again

assembler = VectorAssembler(inputCols=[
    'mass', 'cyl', 'type_dummy', 'density_line', 'density_quad', 'density_cube'
], outputCol='features')
cars = assembler.transform(cars)

+-----------------------------------------------------------------------------+-----------+
|features                                                                     |consumption|
+-----------------------------------------------------------------------------+-----------+
|[1451.0,6.0,1.0,0.0,0.0,0.0,0.0,303.8743455497,63.63860639785,13.32745683724]|9.05       |
|[1129.0,4.0,0.0,0.0,1.0,0.0,0.0,244.2137140385,52.82580879050,11.42673778726]|6.53       |
|[1399.0,4.0,0.0,0.0,1.0,0.0,0.0,307.6753903672,67.66557958374,14.88136784335]|7.84       |
|[1147.0,4.0,0.0,1.0,0.0,0.0,0.0,264.1031545014,60.81122599620,14.00212433714]|7.84       |
+-----------------------------------------------------------------------------+-----------+

Cars: Linear regression

Fit a (standard) Linear Regression model to the training data.

regression = LinearRegression(labelCol='consumption').fit(cars_train)

# RMSE on testing data
0.708699086182001

Examine the coefficients:

regression.coefficients

DenseVector([-0.012, 0.174, -0.897, -1.445, -0.985, -1.071, -1.335, 0.189, -0.780, 1.160])

Cars: Ridge regression

# alpha = 0 | lambda = 0.1 -> Ridge
ridge = LinearRegression(labelCol='consumption', elasticNetParam=0, regParam=0.1)
ridge.fit(cars_train)

# RMSE
0.724535609745491

# Ridge coefficients
DenseVector([ 0.001, 0.137, -0.395, -0.822, -0.450, -0.582, -0.806, 0.008,  0.029, 0.001])
# Linear Regression coefficients
DenseVector([-0.012, 0.174, -0.897, -1.445, -0.985, -1.071, -1.335, 0.189, -0.780, 1.160])

Cars: Lasso regression

# alpha = 1 | lambda = 0.1 -> Lasso
lasso = LinearRegression(labelCol='consumption', elasticNetParam=1, regParam=0.1)
lasso.fit(cars_train)

# RMSE
0.771988667026998

# Lasso coefficients
DenseVector([   0.0,   0.0,    0.0, -0.056,    0.0,    0.0,    0.0, 0.026,    0.0,   0.0])
# Ridge coefficients
DenseVector([ 0.001, 0.137, -0.395, -0.822, -0.450, -0.582, -0.806, 0.008,  0.029, 0.001])
# Linear Regression coefficients
DenseVector([-0.012, 0.174, -0.897, -1.445, -0.985, -1.071, -1.335, 0.189, -0.780, 1.160])

Regularization ? simple model

Machine Learning with PySpark