Correlación
Introducción a la estadística

George Boorman
Curriculum Manager, DataCamp
Relaciones entre dos variables
Coeficiente de correlación de Pearson
- Lo publicó Karl Pearson en 1896.
- Cuantifica la fuerza de una relación entre dos variables.
- Número entre menos uno y uno.
- La magnitud corresponde a la fuerza de la relación.
- El signo (+ o -) corresponde a la dirección de la relación.
1 https://royalsocietypublishing.org/doi/10.1098/rsta.1896.0007
Relaciones lineales
- Lineal = cambios proporcionales entre las variables dependientes e independientes.
Valores = fuerza de la relación
0,99 (relación muy fuerte)
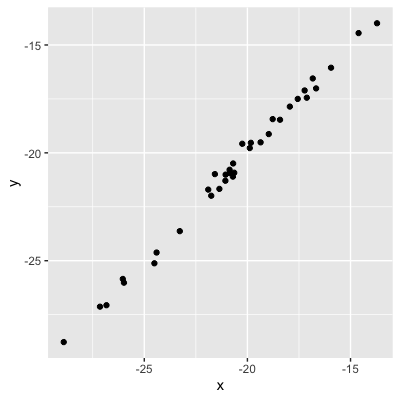
Valores = fuerza de la relación
0,99 (relación muy fuerte)

0,75 (relación fuerte)
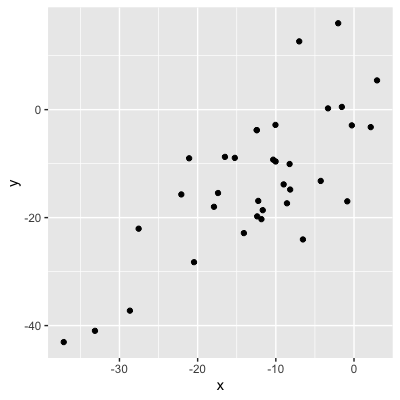
Valores = fuerza de la relación
0,56 (relación moderada)
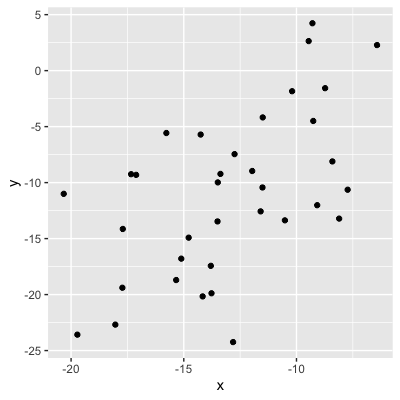
Valores = fuerza de la relación
0,56 (relación moderada)

0,21 (relación débil)
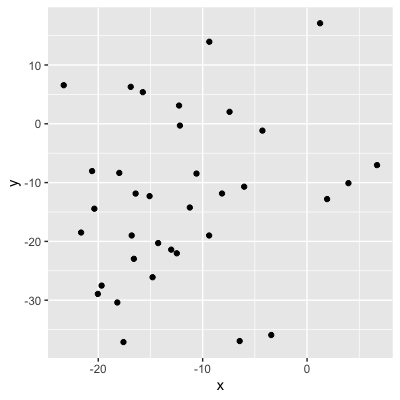
Valores = fuerza de la relación
0,04 (sin relación)
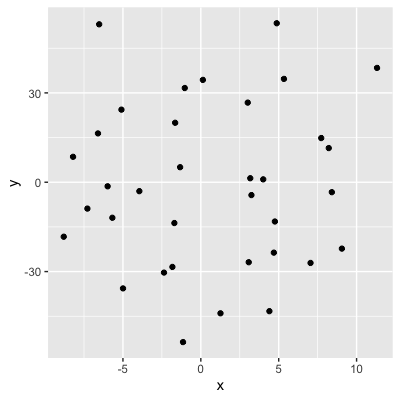
- Conocer el valor de x no nos dice nada sobre y.
Signo = dirección
0,75: a medida que x aumenta, y aumenta

-0,75: a medida que x aumenta, y disminuye
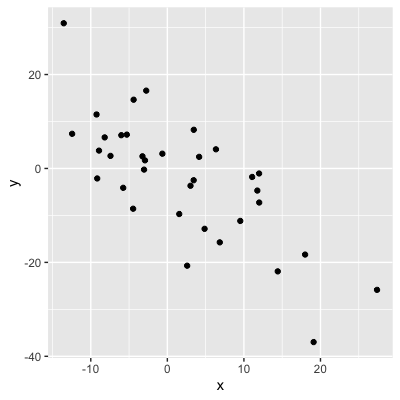
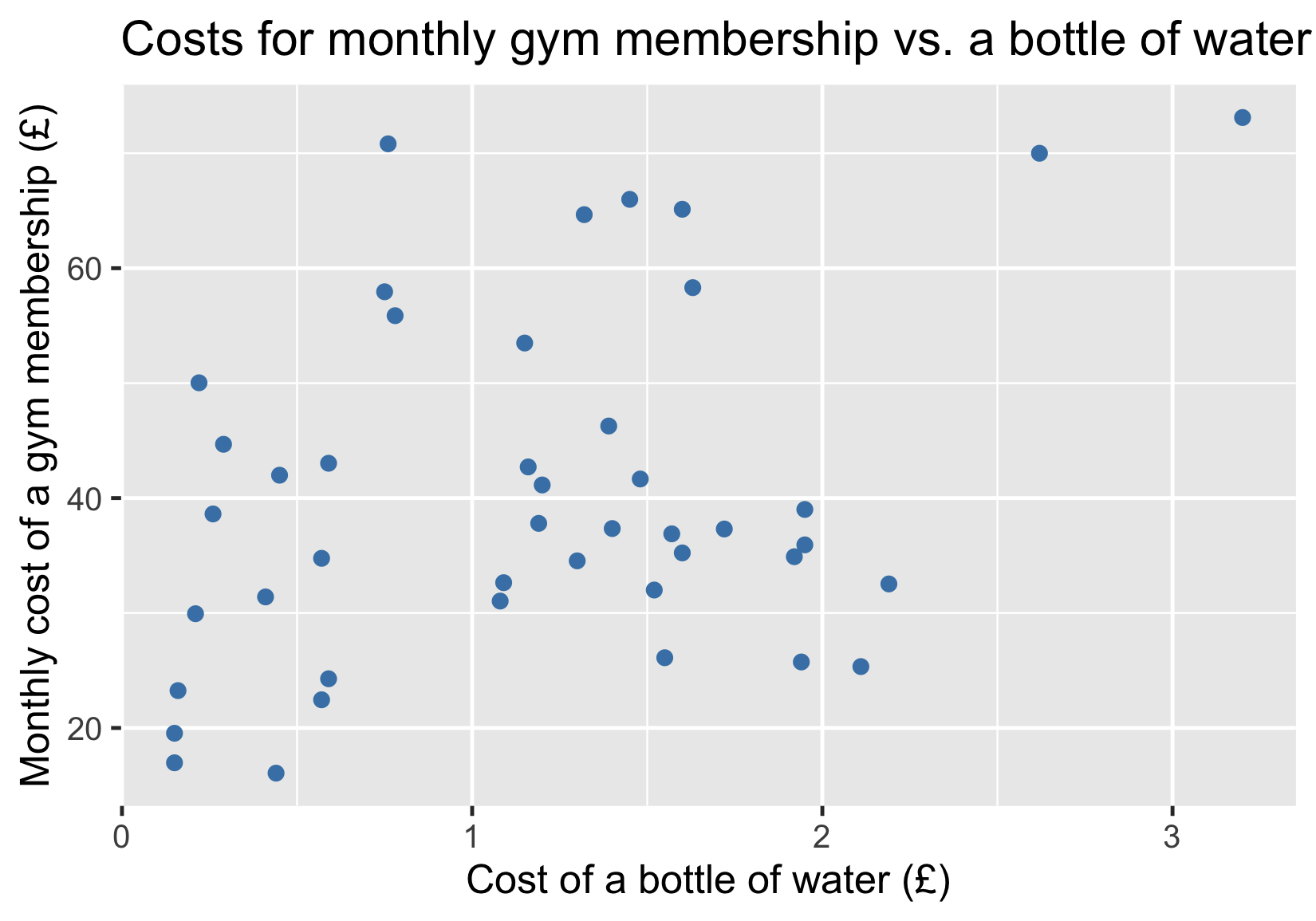
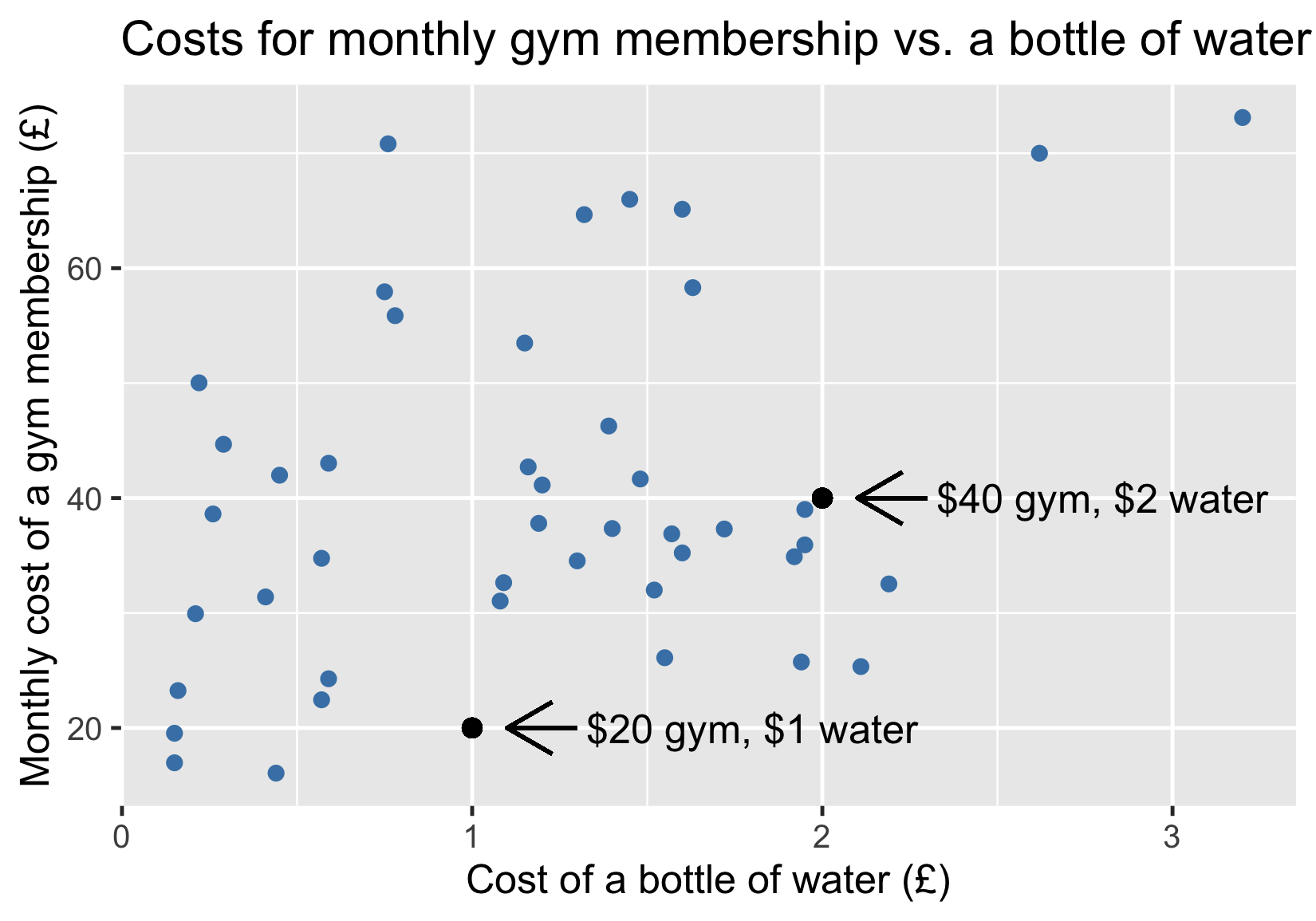
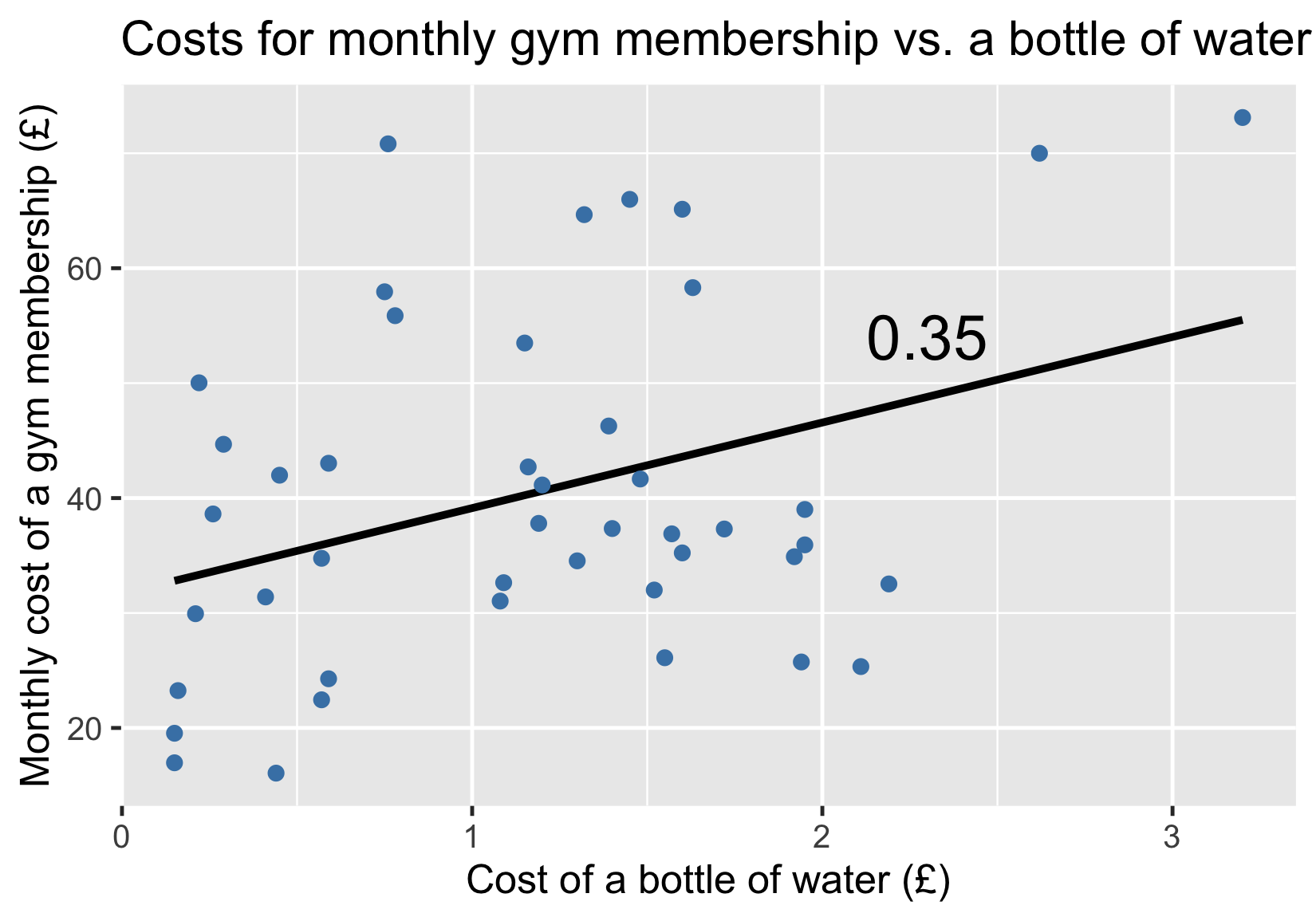
Costes del gimnasio frente a costes del agua

Añadir una línea de tendencia
Esperanza de vida frente al coste de una botella de agua
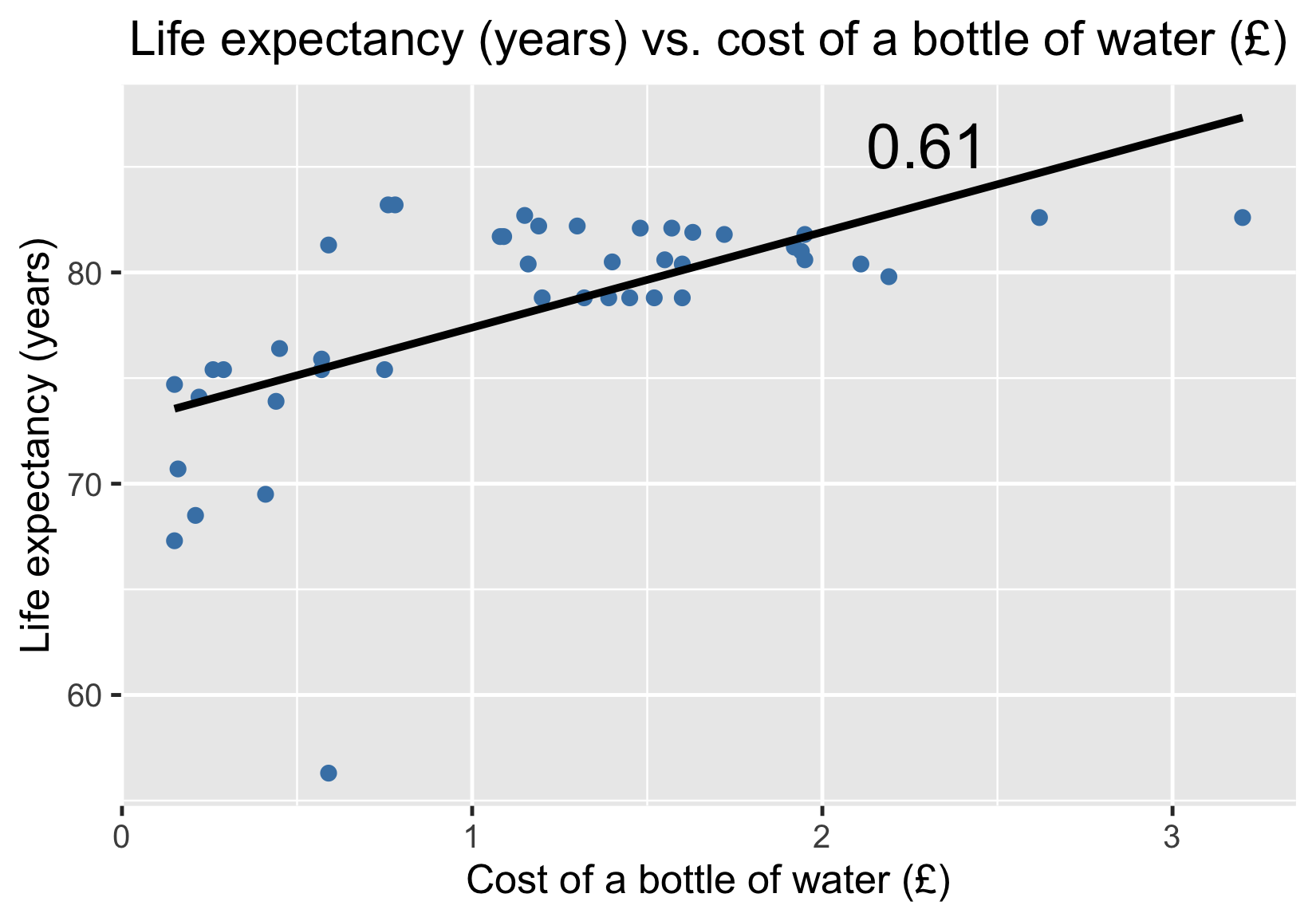
La correlación no implica causalidad.
- ¿El aumento del coste del agua provocará un aumento de la esperanza de vida?


- La correlación no implica causalidad.
1 Crédito de la imagen: https://unsplash.com/@micheile; https://unsplash.com/@jon_chng
Variables de confusión
¿Qué otros factores podrían estar afectando la esperanza de vida?
- Una botella de agua cuesta más en países con economías fuertes.
- Estos países suelen ofrecer acceso a una asistencia sanitaria de alta calidad.
La fortaleza de la economía podría ser una variable de confusión.
- Una variable de confusión no se mide, pero puede afectar a la relación entre nuestras variables.

¡Vamos a practicar!
Introducción a la estadística

