La distribución binomial
Introducción a la estadística

George Boorman
Curriculum Manager, DataCamp
Lanzar una moneda
Resultados binarios
Lanzar una moneda muchas veces
| Lanzamiento de moneda | Resultado |
|---|---|
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 0 |
| 6 | 0 |
| 7 | 1 |
| 8 | 0 |
| 9 | 1 |
| 10 | 1 |
Distribución binomial
Distribución de probabilidad del número de aciertos en una secuencia de sucesos independientes.
Por ejemplo, el número de caras en una secuencia de lanzamientos de una moneda.
Se describe con $n$ y $p$.
- $n$: número total de sucesos
- $p$: probabilidad de acierto
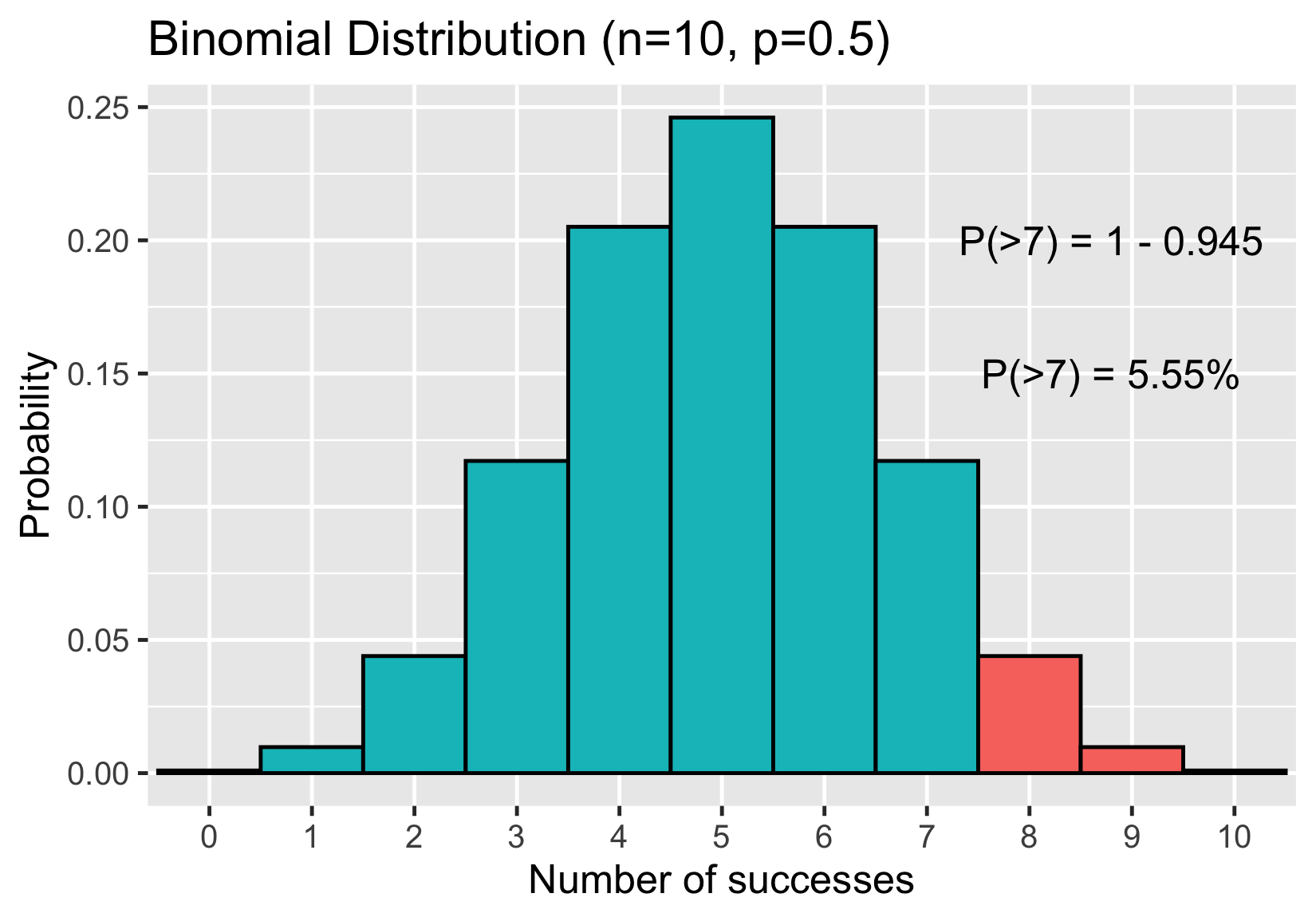
Distribución binomial
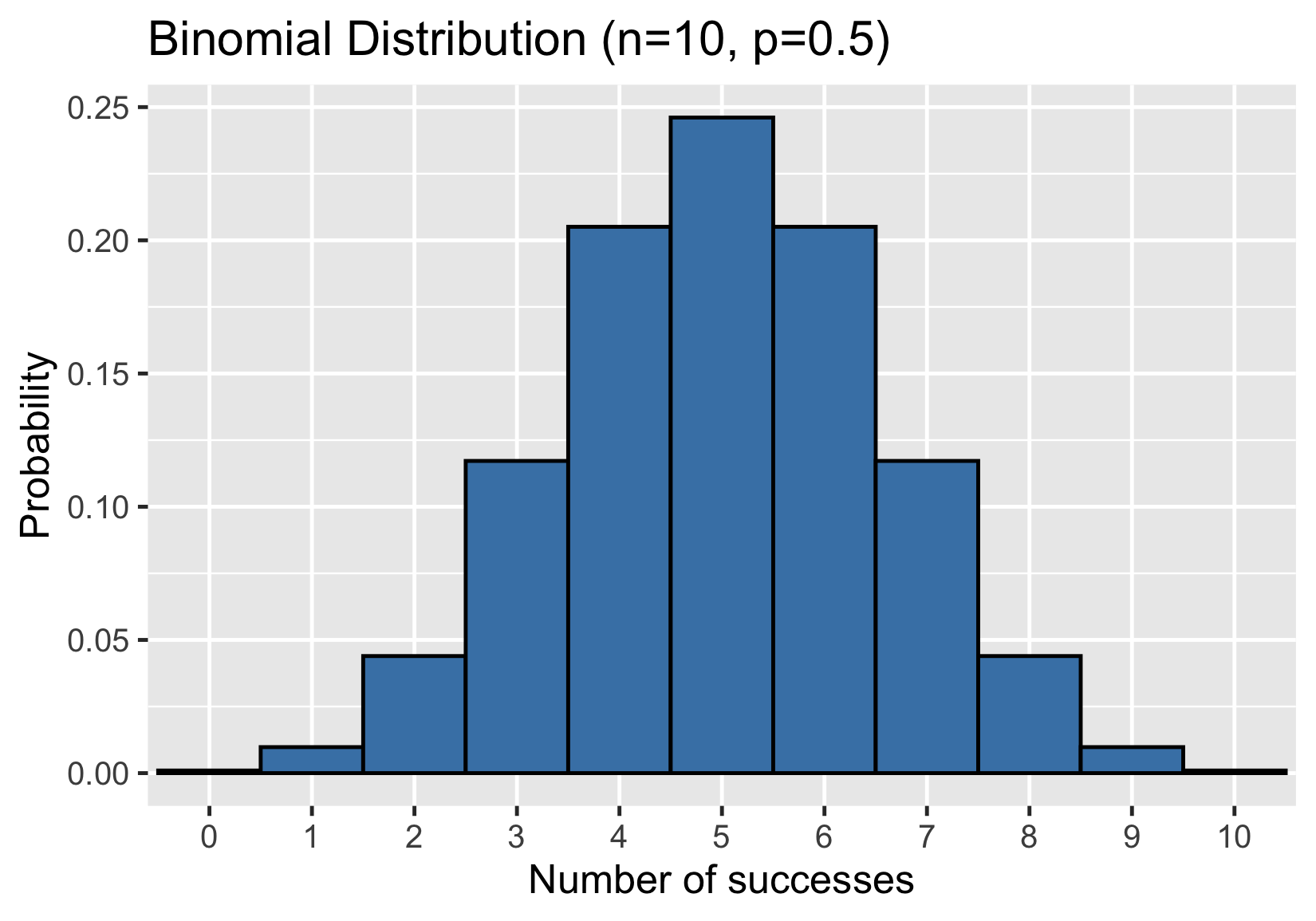
Probabilidad de que salgan 7 caras o menos
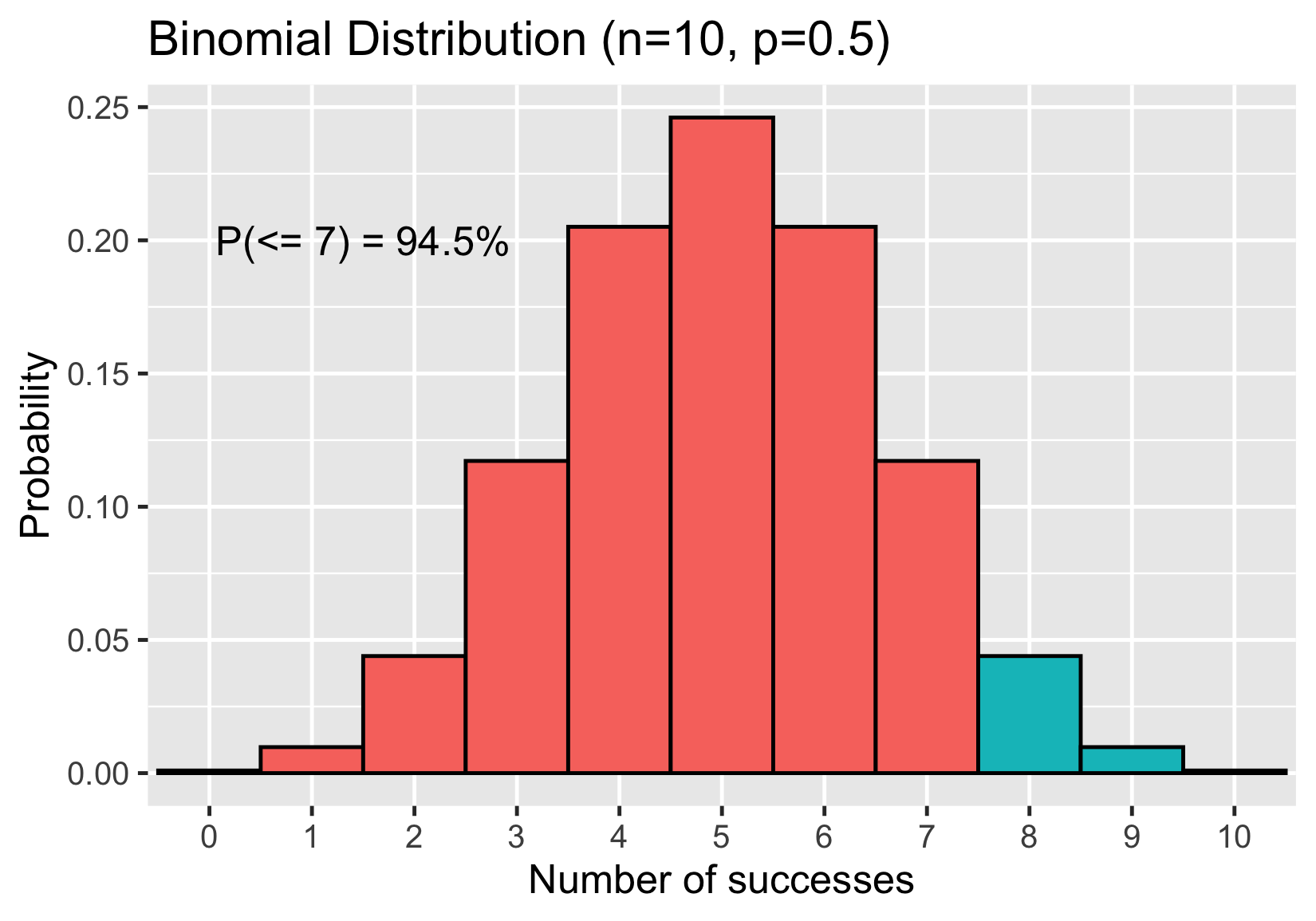
Probabilidad de obtener 8 o más caras
Valor esperado
${Expected \ value} = n \times p$
Número esperado de caras tras 10 tiradas $= 10 \times 0,5 = 5$
Si no conocemos $p$, pero conocemos $n$ y el valor esperado:
${p} = \frac{valor esperado}{n} $
Independencia
La distribución binomial es una distribución de probabilidad del número de aciertos en una secuencia de sucesos independientes.
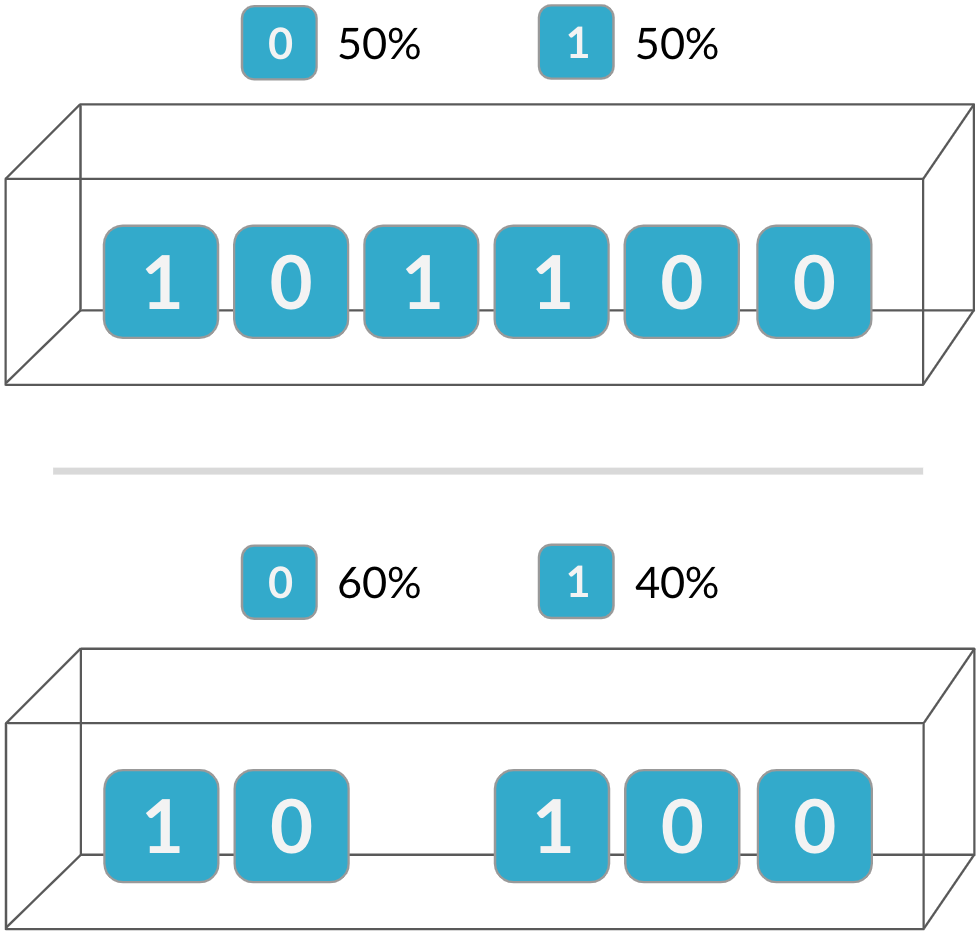
Independencia
La distribución binomial es una distribución de probabilidad del número de aciertos en una secuencia de sucesos independientes.
Las probabilidades de que se produzca el segundo suceso se ven alteradas por el resultado del primero.
Si los sucesos no son independientes, ¡la distribución binomial no se aplica!
Aplicaciones generales
La distribución binomial se puede utilizar para sucesos independientes que producen resultados binarios.
- Ensayo clínico para medir la eficacia de un medicamento.
- Es eficaz o no lo es.
- Apostar por el resultado de un partido deportivo.
- Se puede ganar o perder.

¡Vamos a practicar!
Introducción a la estadística

