Distribuciones discretas
Introducción a la estadística

George Boorman
Curriculum Manager, DataCamp

Tirar los dados
Elegir a los vendedores

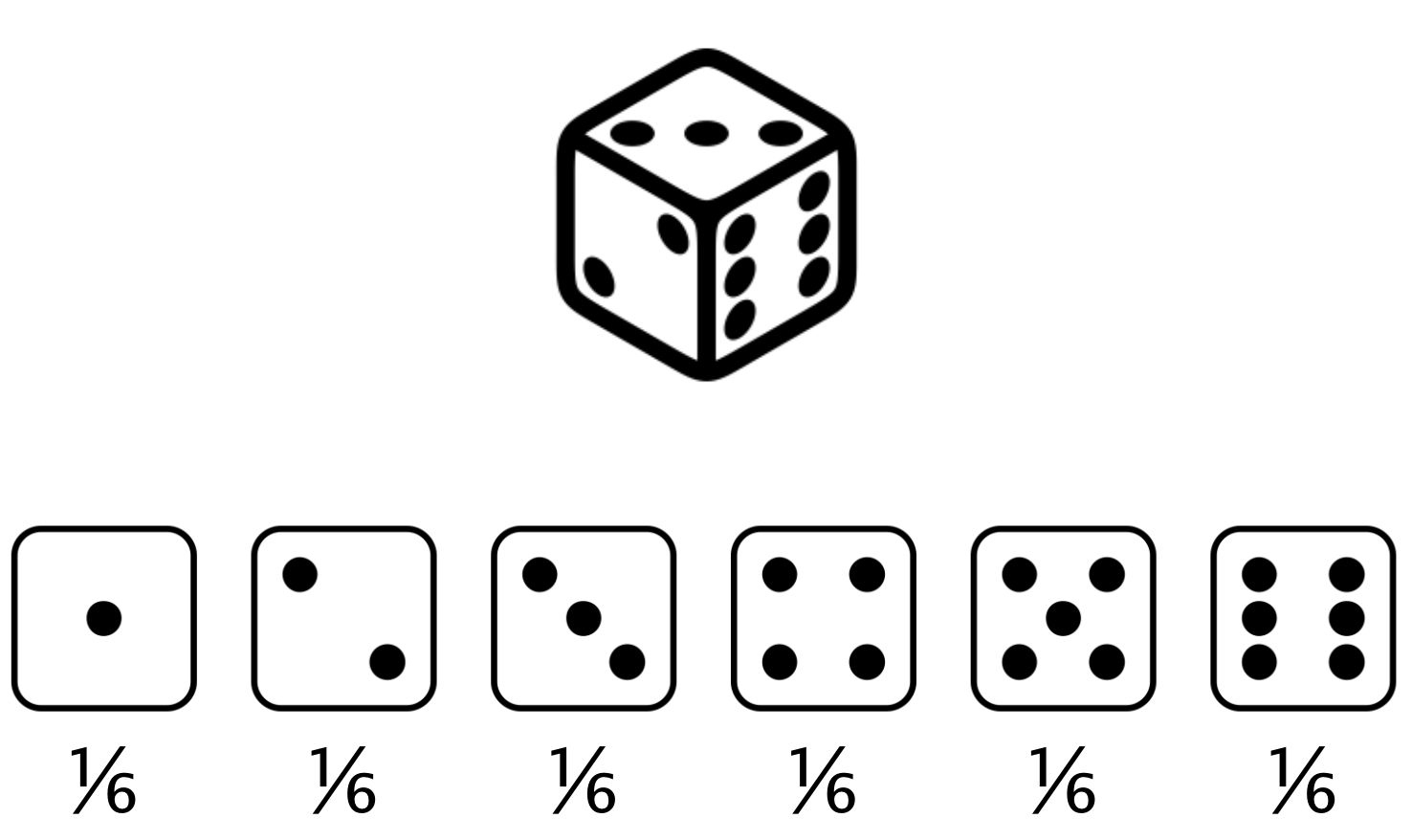
Distribución de probabilidad
Describe la probabilidad de cada resultado posible en una situación.
Valor esperado: la media de una distribución de probabilidad.
Valor esperado de una tirada justa = $(1 \times \frac{1}{6}) + (2 \times \frac{1}{6}) +(3 \times \frac{1}{6}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3,5$
¿Por qué son importantes las distribuciones de probabilidad?
- Nos ayudan a cuantificar el riesgo y a tomar decisiones informadas.
- Ampliamente utilizadas en la comprobación de hipótesis.
- Probabilidad de que los resultados se hayan producido por casualidad.
Visualizar una distribución de probabilidad
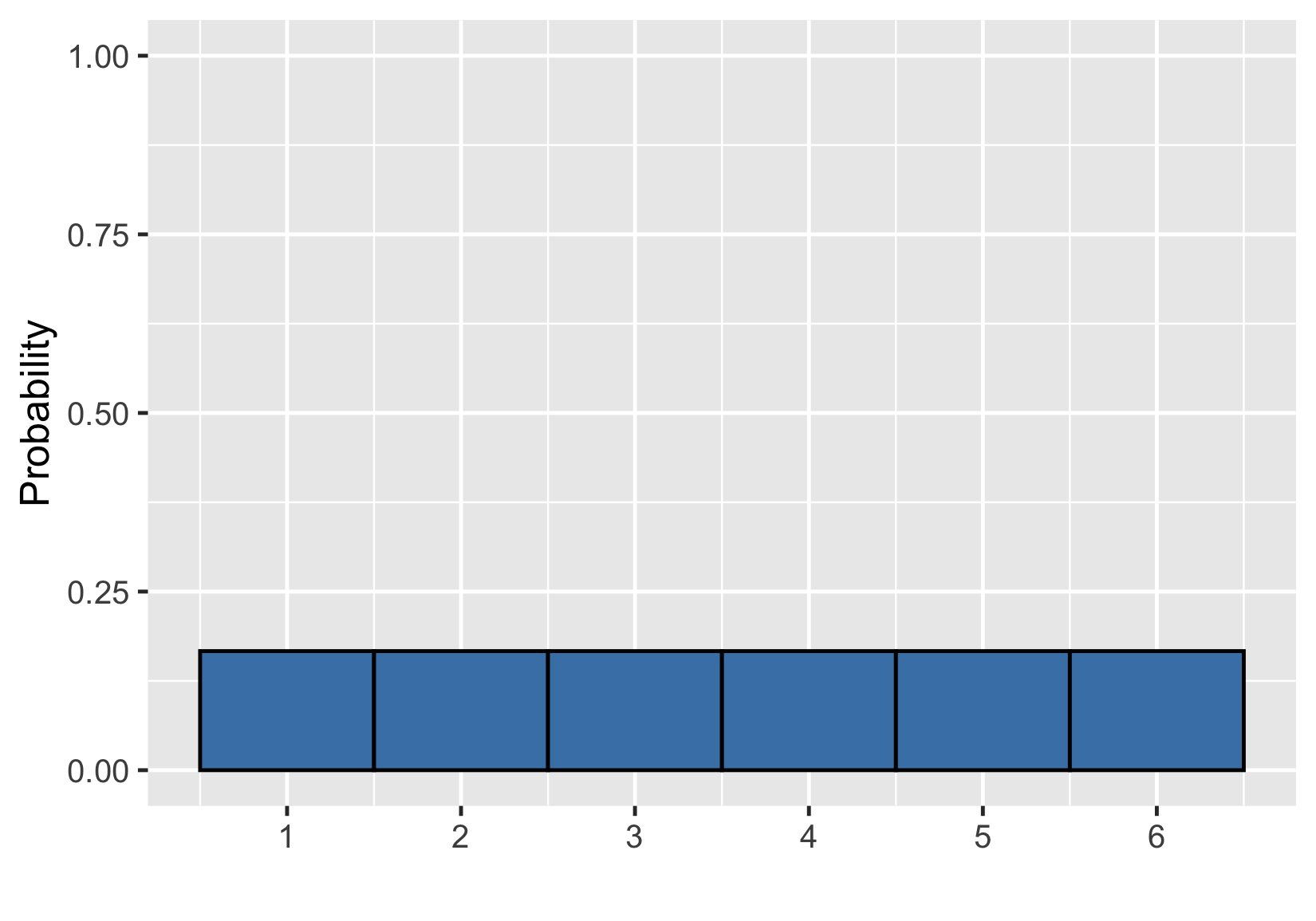
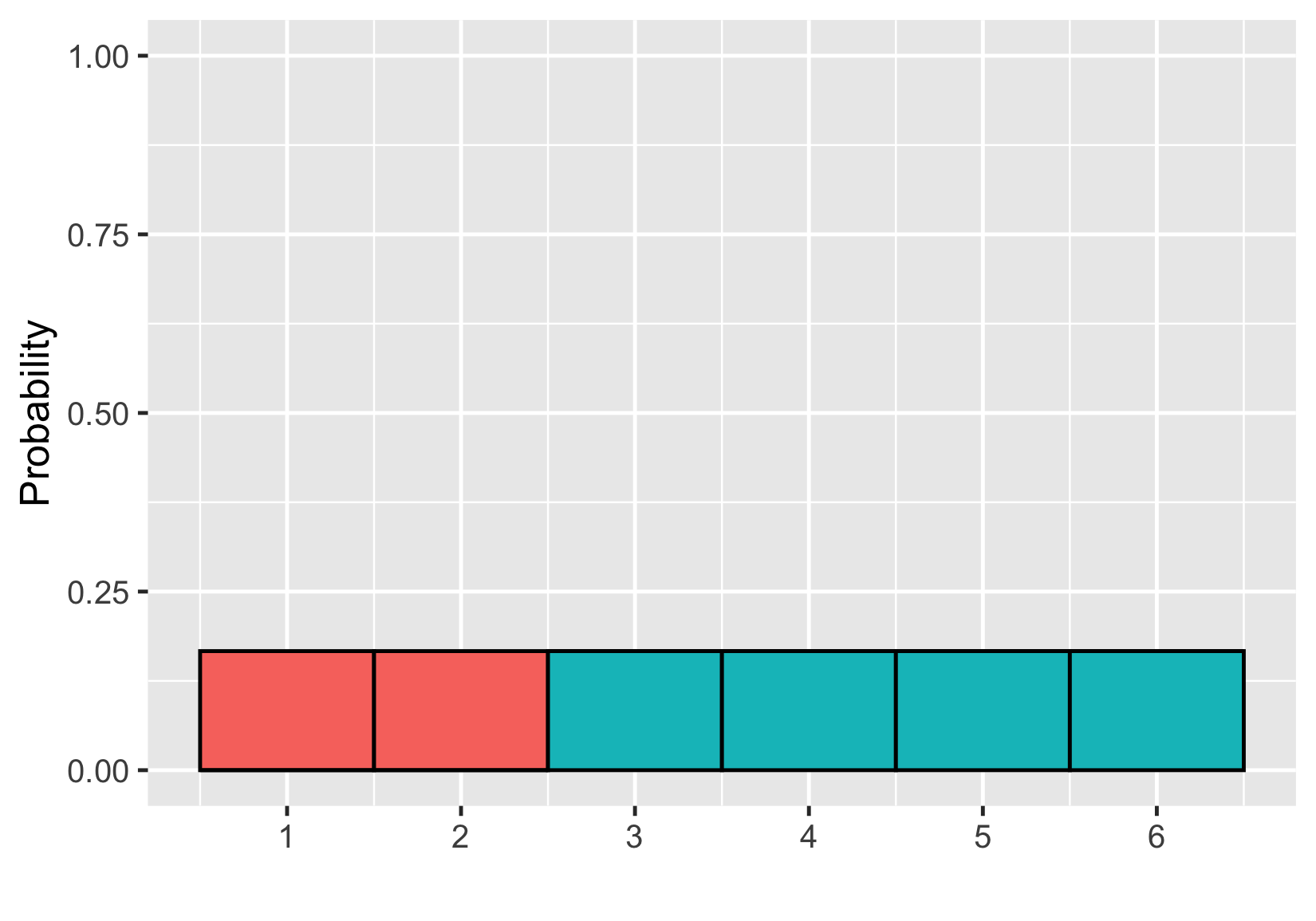
Probabilidad = área
$$P(\text{tirada de un dado}) \le 2 = ~?$$
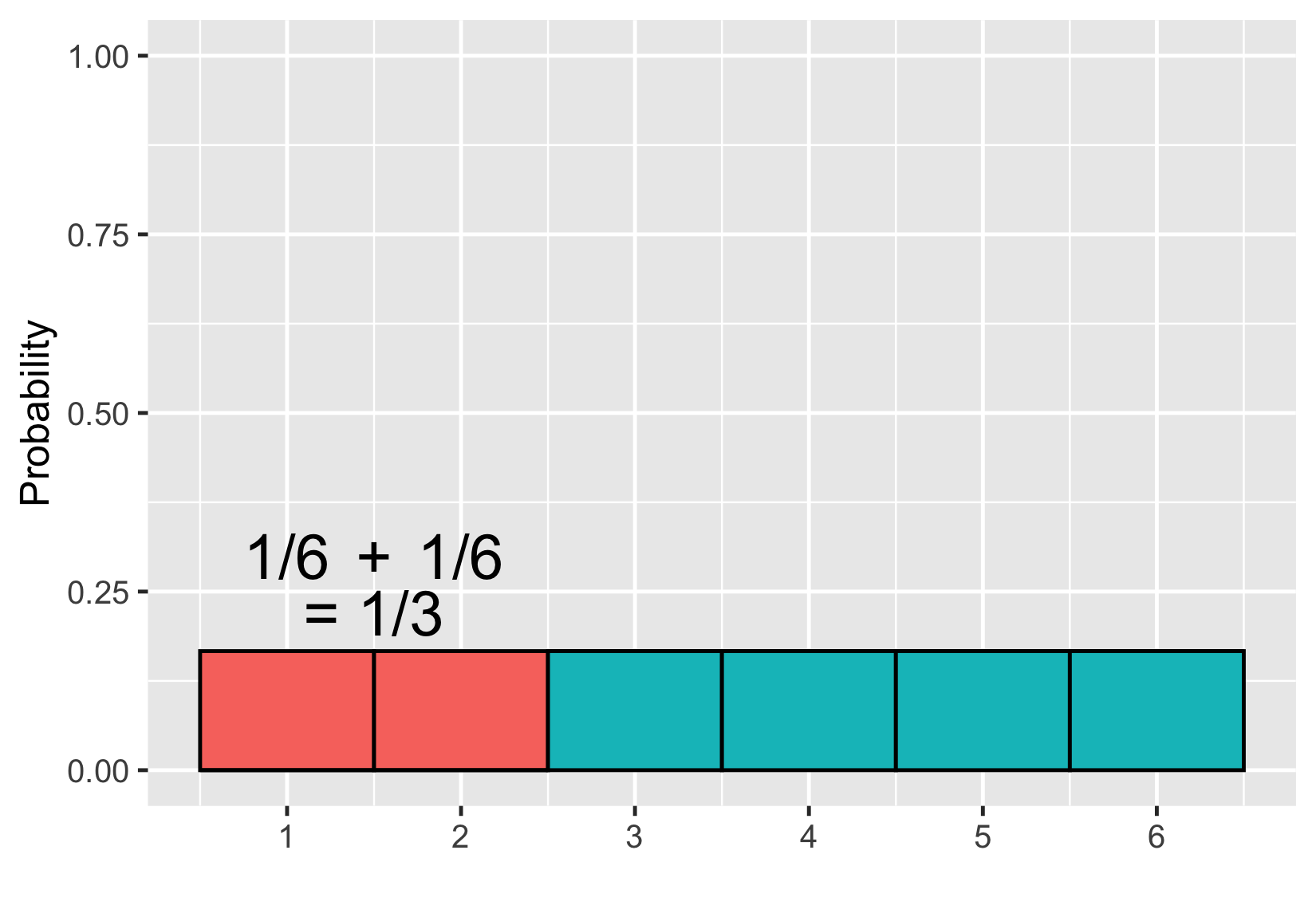
Probabilidad = área
$$P(\text{tirada de un dado}) \le 2 = 1/3$$
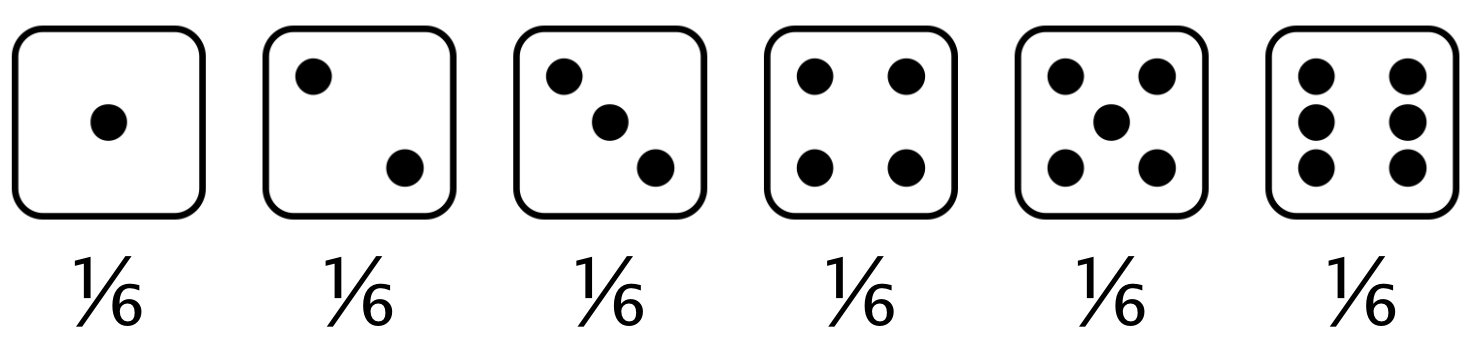
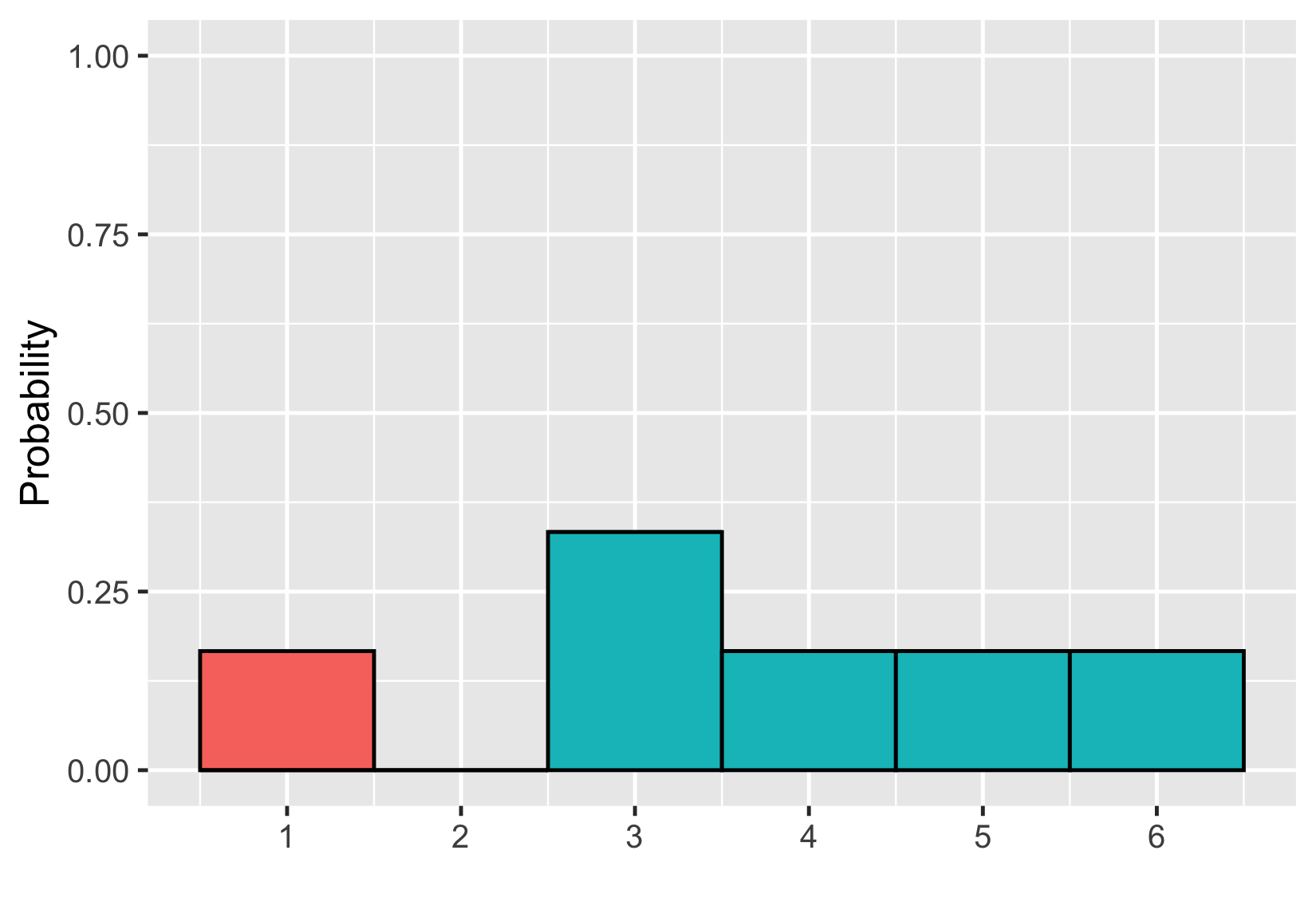
Dado desigual
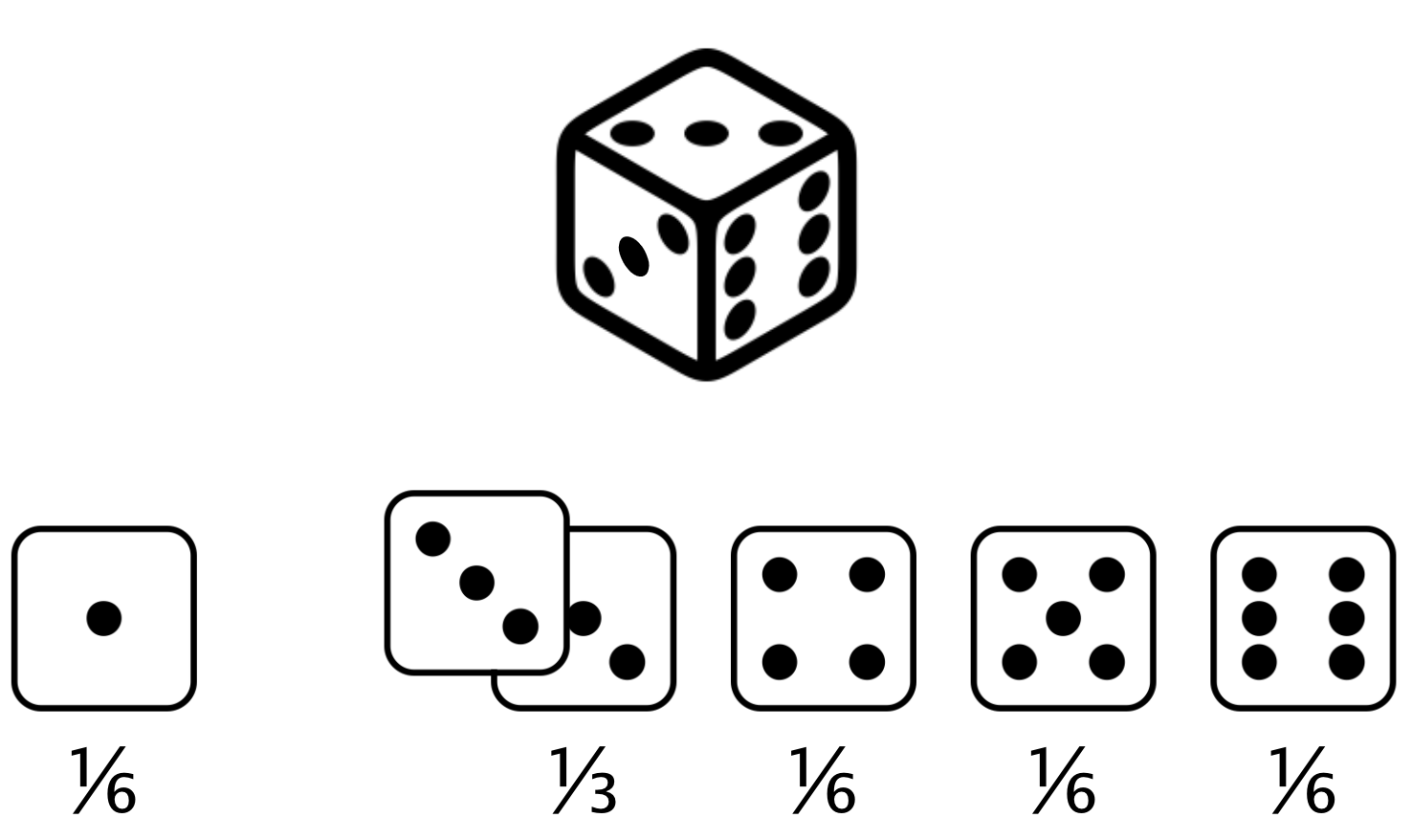
Valor esperado de la tirada desigual = $(1 \times \frac{1}{6}) +(2 \times 0) +(3 \times \frac{1}{3}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3,67$.
Visualizar probabilidades desiguales
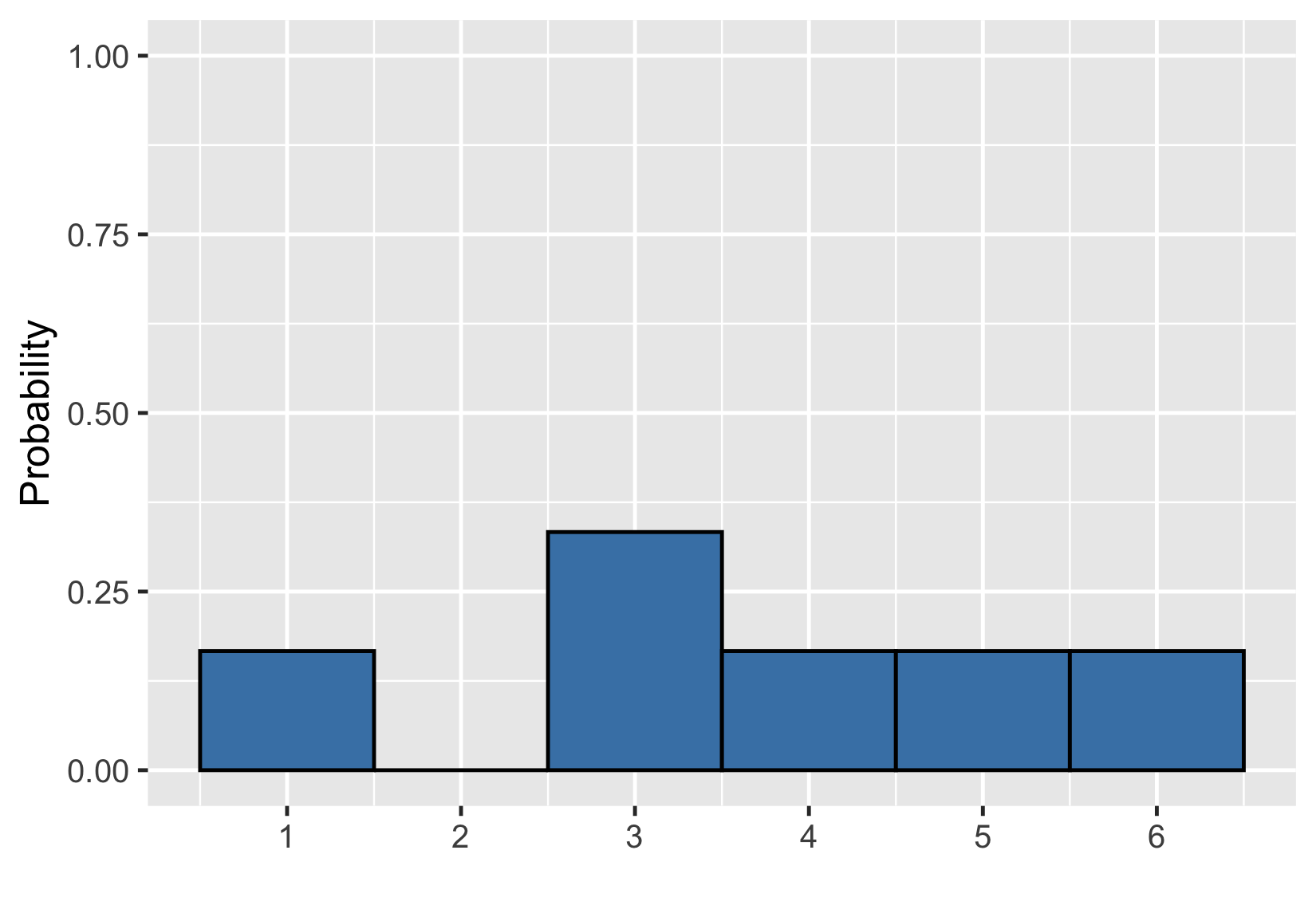
Añadir áreas
$$P(\text{uneven die roll}) \le 2 = ~?$$
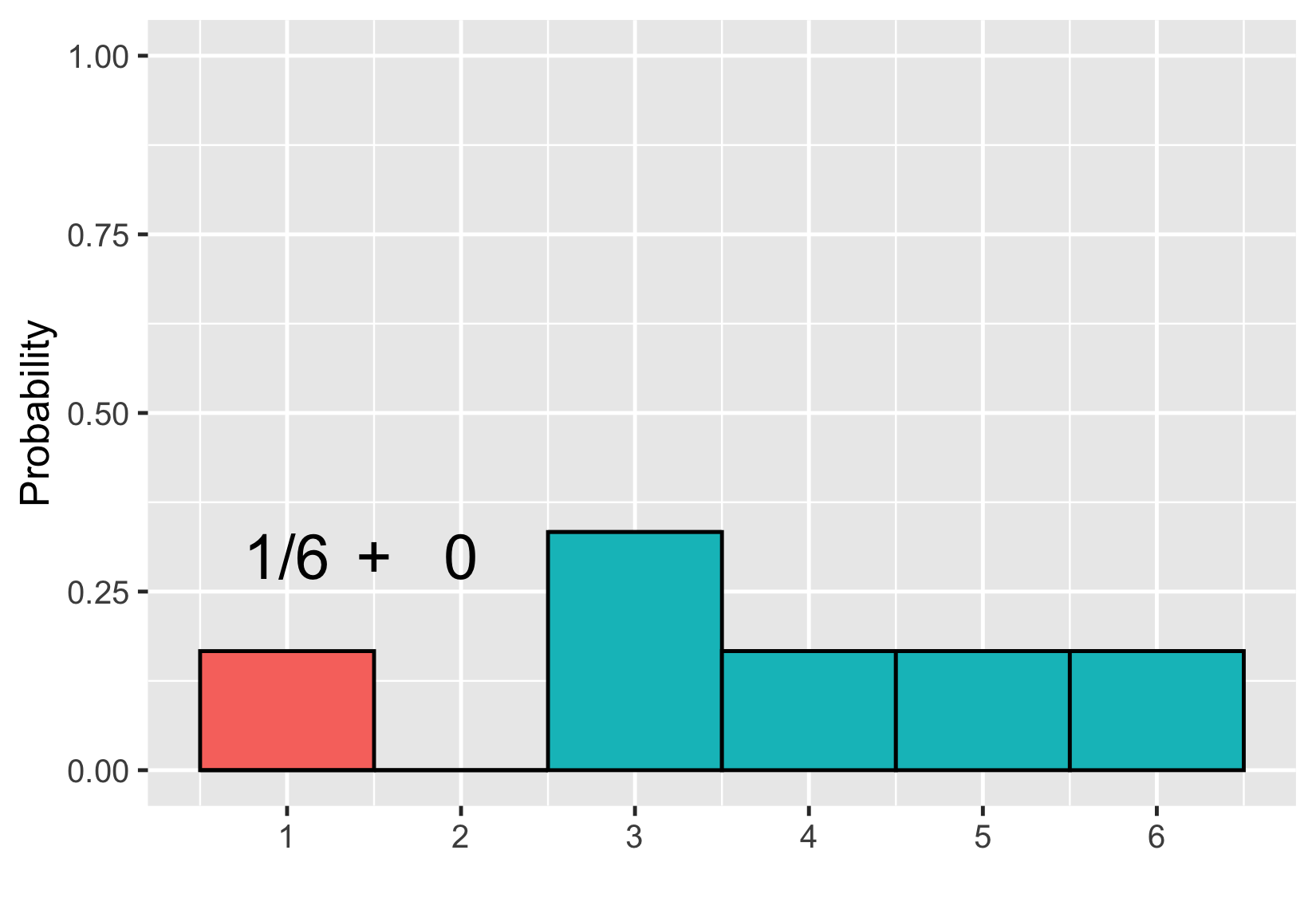
Añadir áreas
$$P(\text{uneven die roll}) \le 2 = 1/6$$
Distribuciones de probabilidad discretas
Describen la probabilidad de resultados discretos
Dado justo
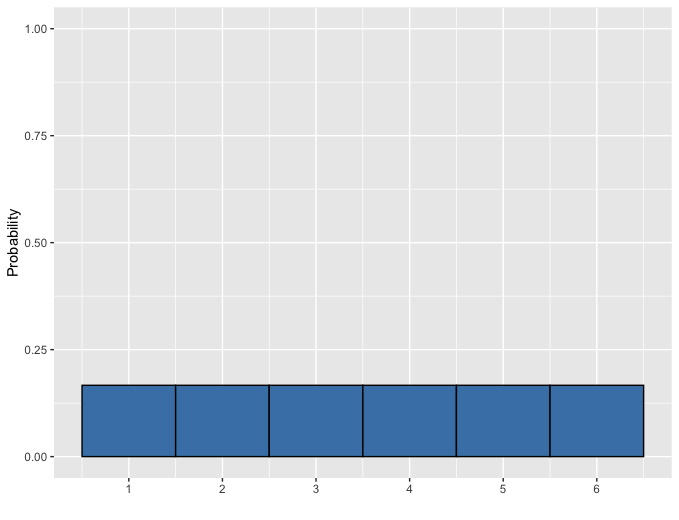
Distribución uniforme discreta
Dado desigual
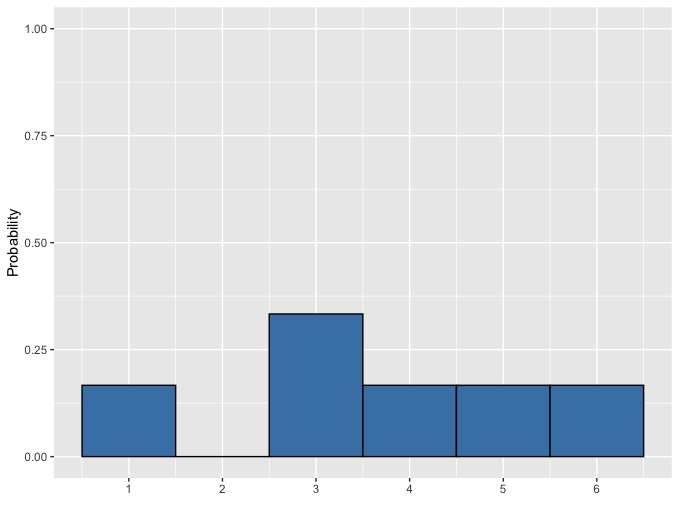
Muestreo a partir de una distribución discreta
| Tirada | Resultado |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
$ {Media} = 3,5 $
| Tirada | Resultado |
|---|---|
| 1 | 3 |
| 2 | 1 |
| 3 | 2 |
| 4 | 4 |
| 5 | 6 |
| 6 | 3 |
| 7 | 2 |
| 8 | 2 |
| 9 | 2 |
| 10 | 5 |
Visualizar una muestra
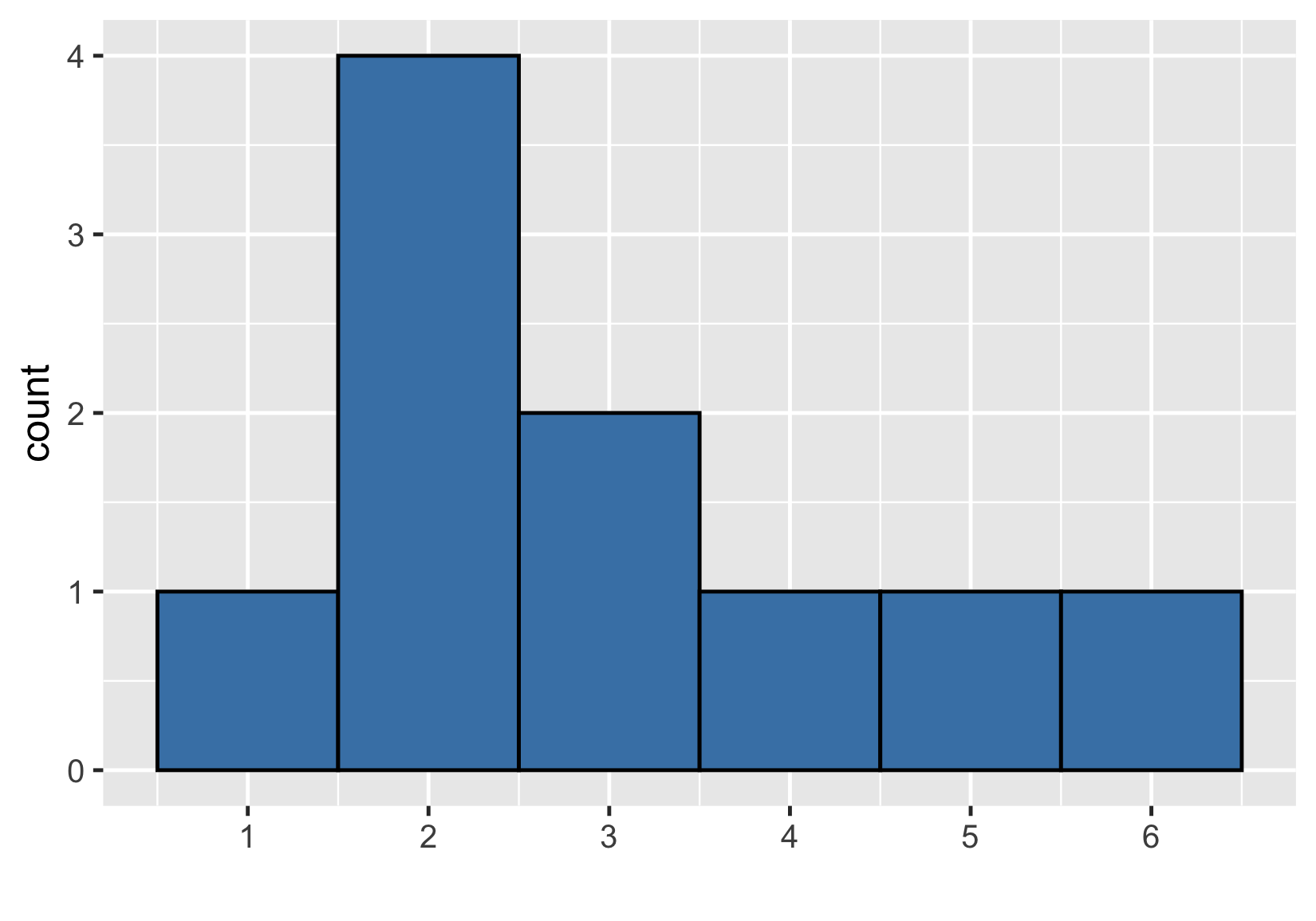
Distribución de muestras frente a distribución teórica

$ {Media } = 3,0 $

$ {Media} = 3,5 $
Una muestra mayor
Muestra de 100 tiradas
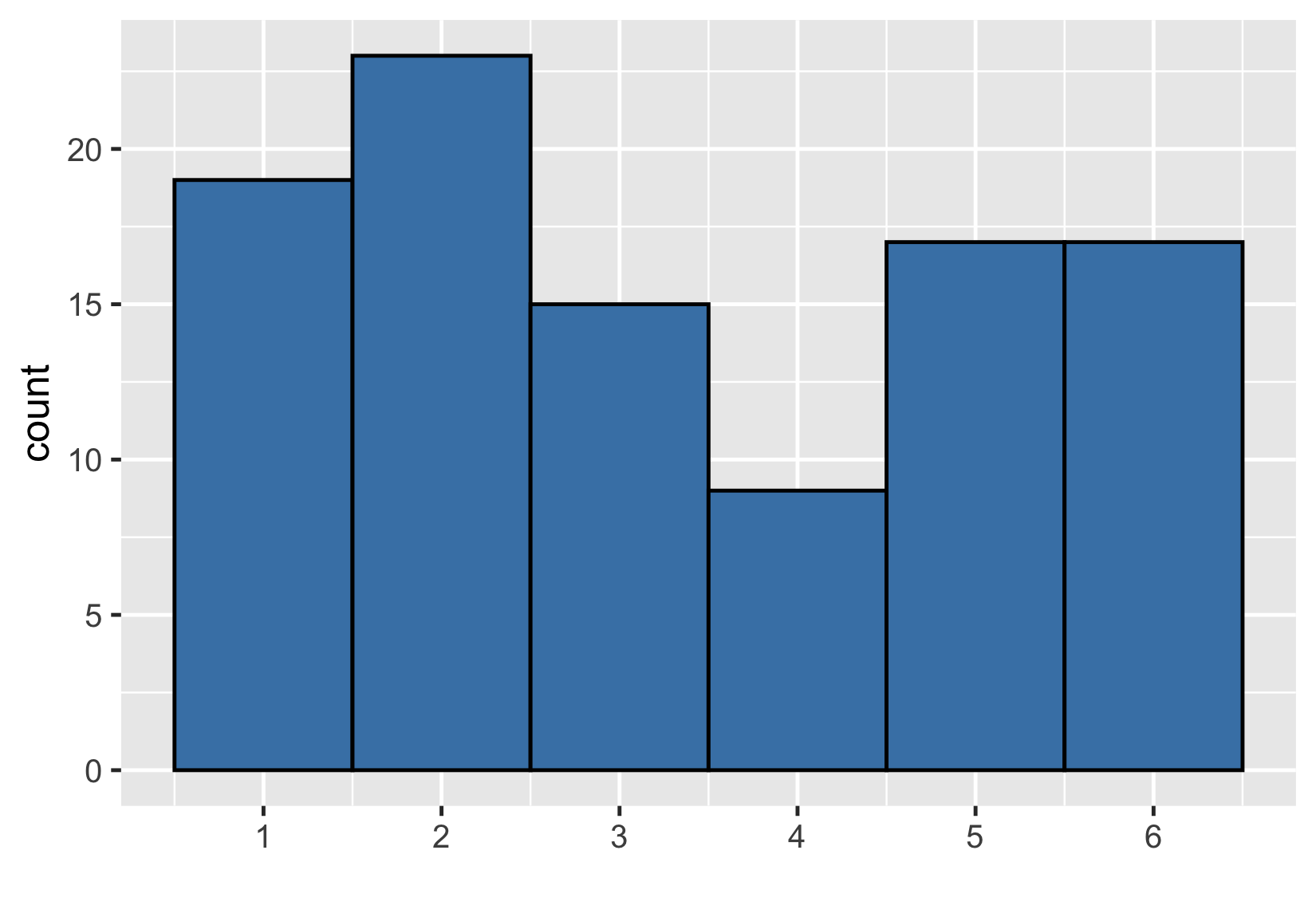
$ {Media} = 3,33 $
Una muestra aún mayor
Muestra de 1000 tiradas
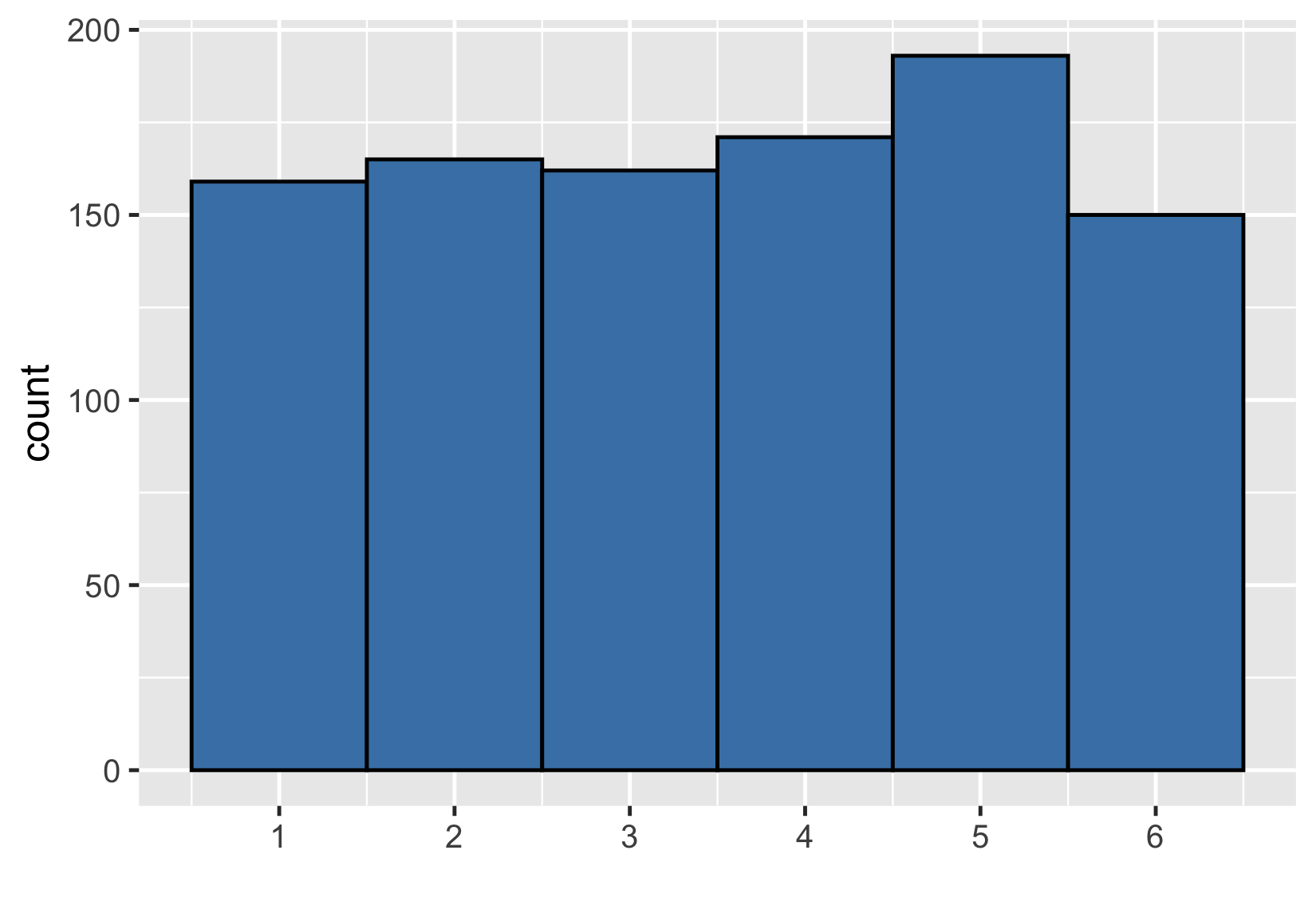
$ {Media} = 3,52 $
Ley de los grandes números
Conforme aumente el tamaño de la muestra, la media muestral se aproximará al valor esperado.
| Tamaño de la muestra | Media |
|---|---|
| 10 | 3,00 |
| 100 | 3,33 |
| 1000 | 3,52 |
¡Vamos a practicar!
Introducción a la estadística

