Probabilidad condicional
Introducción a la estadística

George Boorman
Curriculum Manager, DataCamp
Varias reuniones
Muestreo sin sustitución

Varias reuniones
Muestreo sin sustitución
$$P(\text{Claire}) = \frac{1}{3} = 33\%$$
Hechos dependientes
La probabilidad del segundo suceso se ve afectada por el resultado del primer suceso.

Hechos dependientes
La probabilidad del segundo suceso se ve afectada por el resultado del primer suceso.
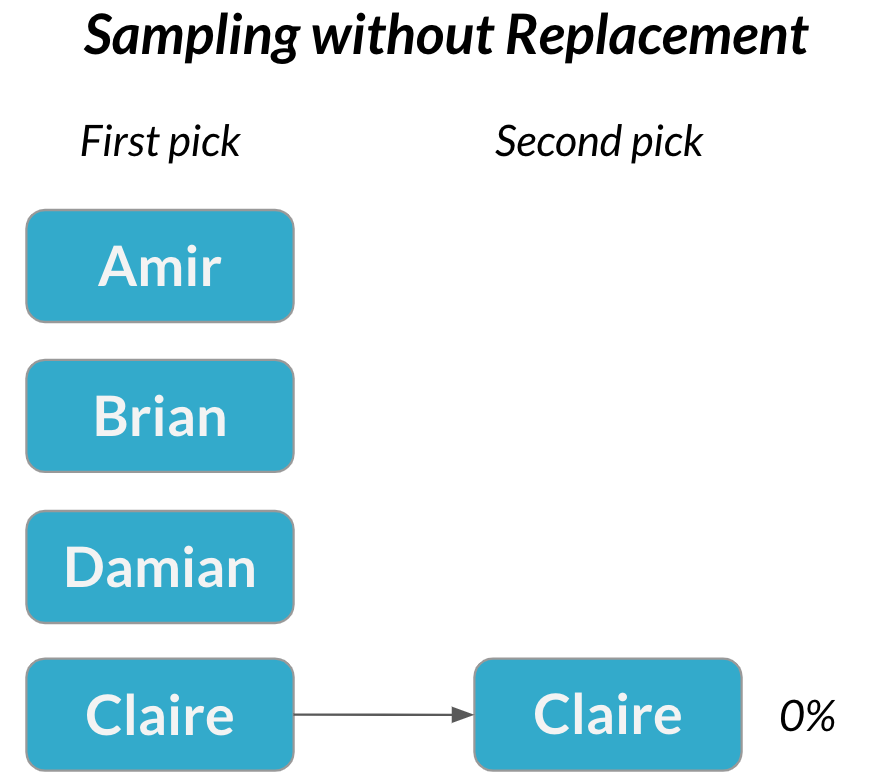
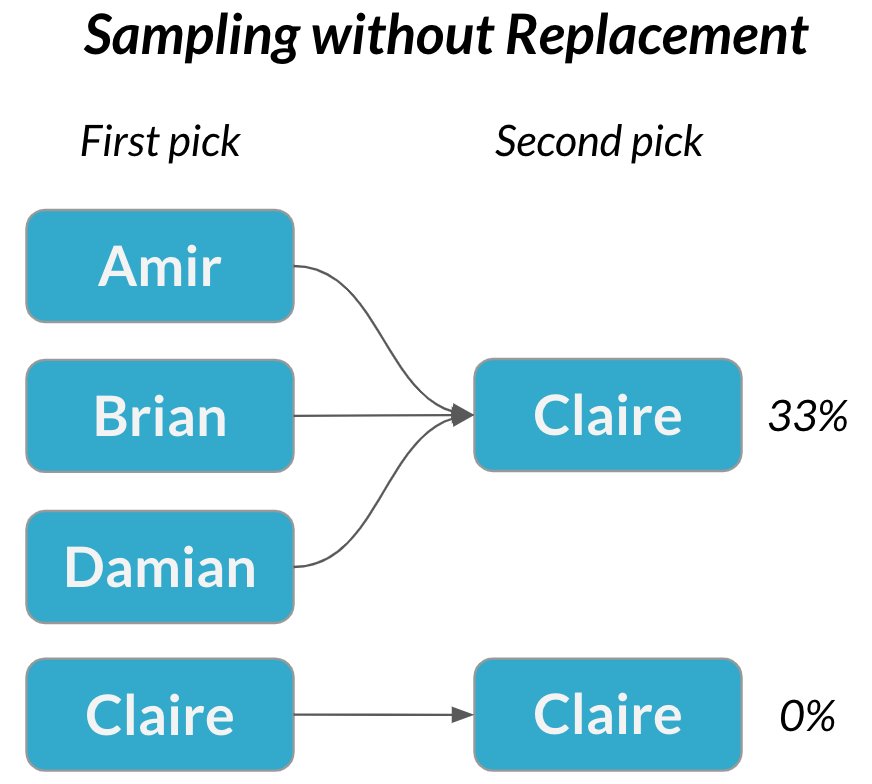
Hechos dependientes
La probabilidad del segundo suceso se ve afectada por el resultado del primer suceso.
Muestreo sin sustitución = cada selección es dependiente
Probabilidad condicional
La probabilidad condicional se utiliza para calcular la probabilidad de sucesos dependientes.
- La probabilidad de que ocurra un evento depende del resultado de otro.

Diagramas de Venn
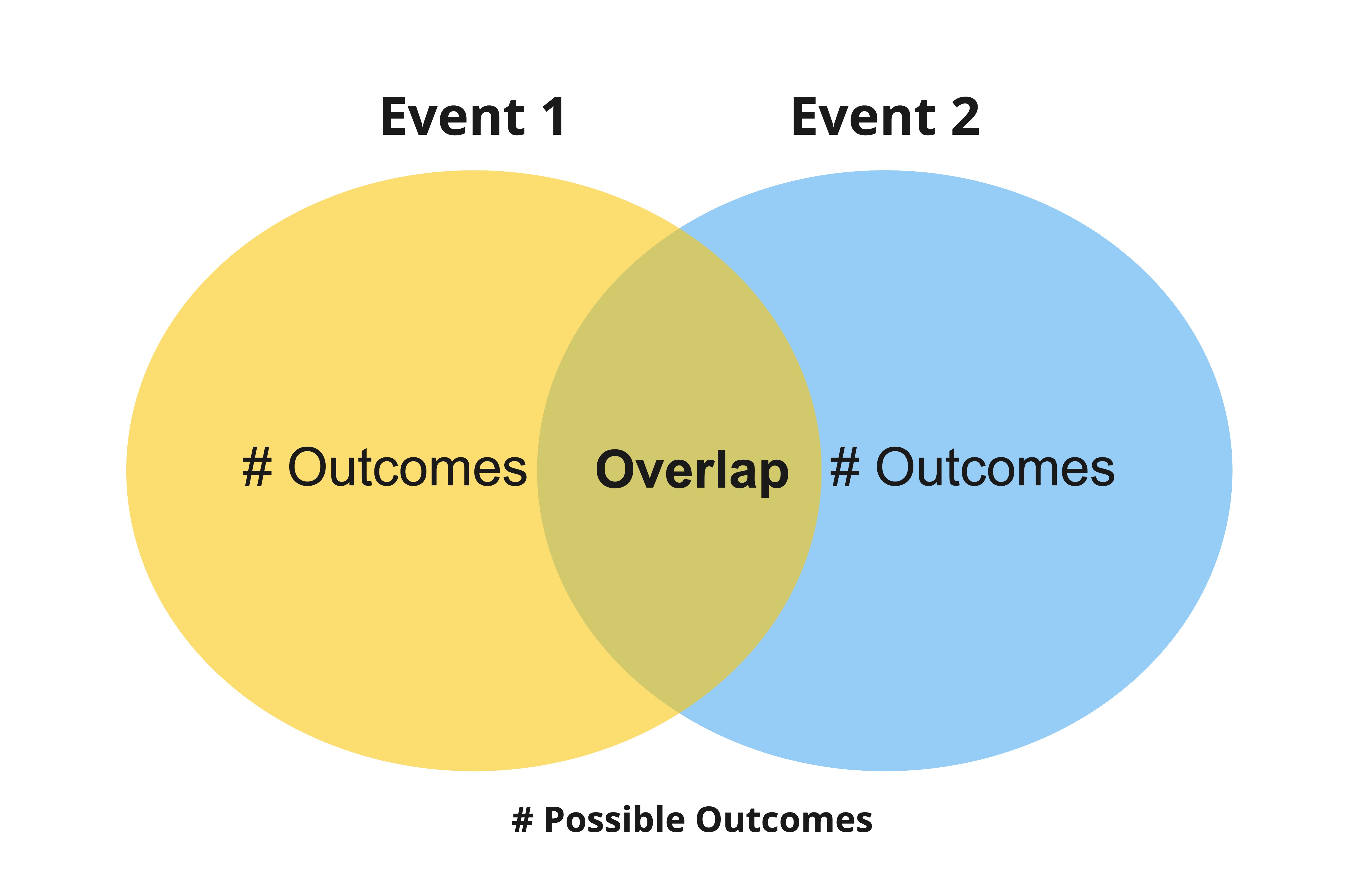
Ventas de cocina de más de $150
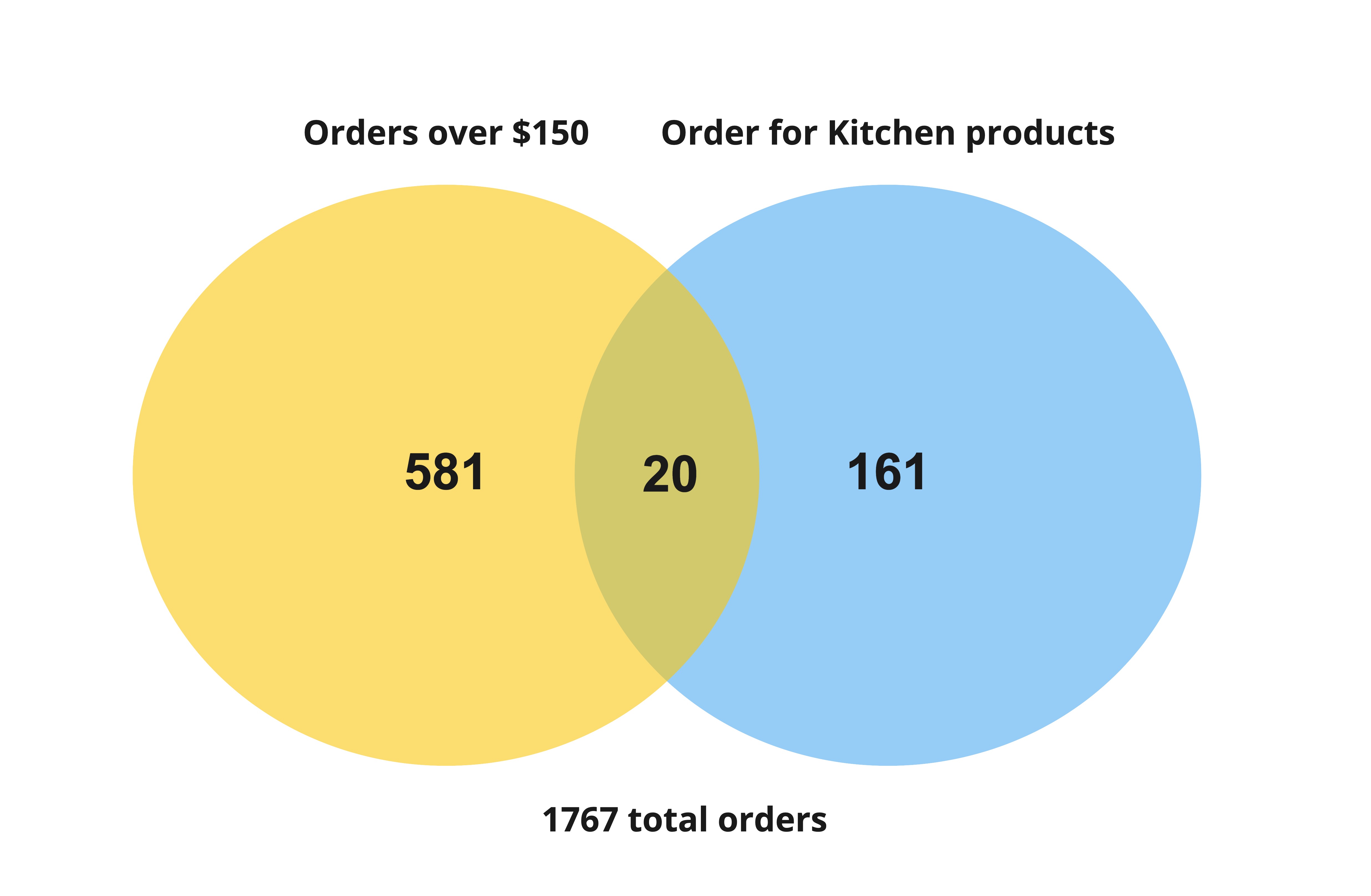
Ventas de cocina de más de $150

$$P(Pedido cocina > 150 |) = \frac{\frac{20}{1767}}{\frac{181}{1767}}$$
$$P(Pedido cocina > 150 |) = \frac{20}{181} $$
El orden de los sucesos es importante.
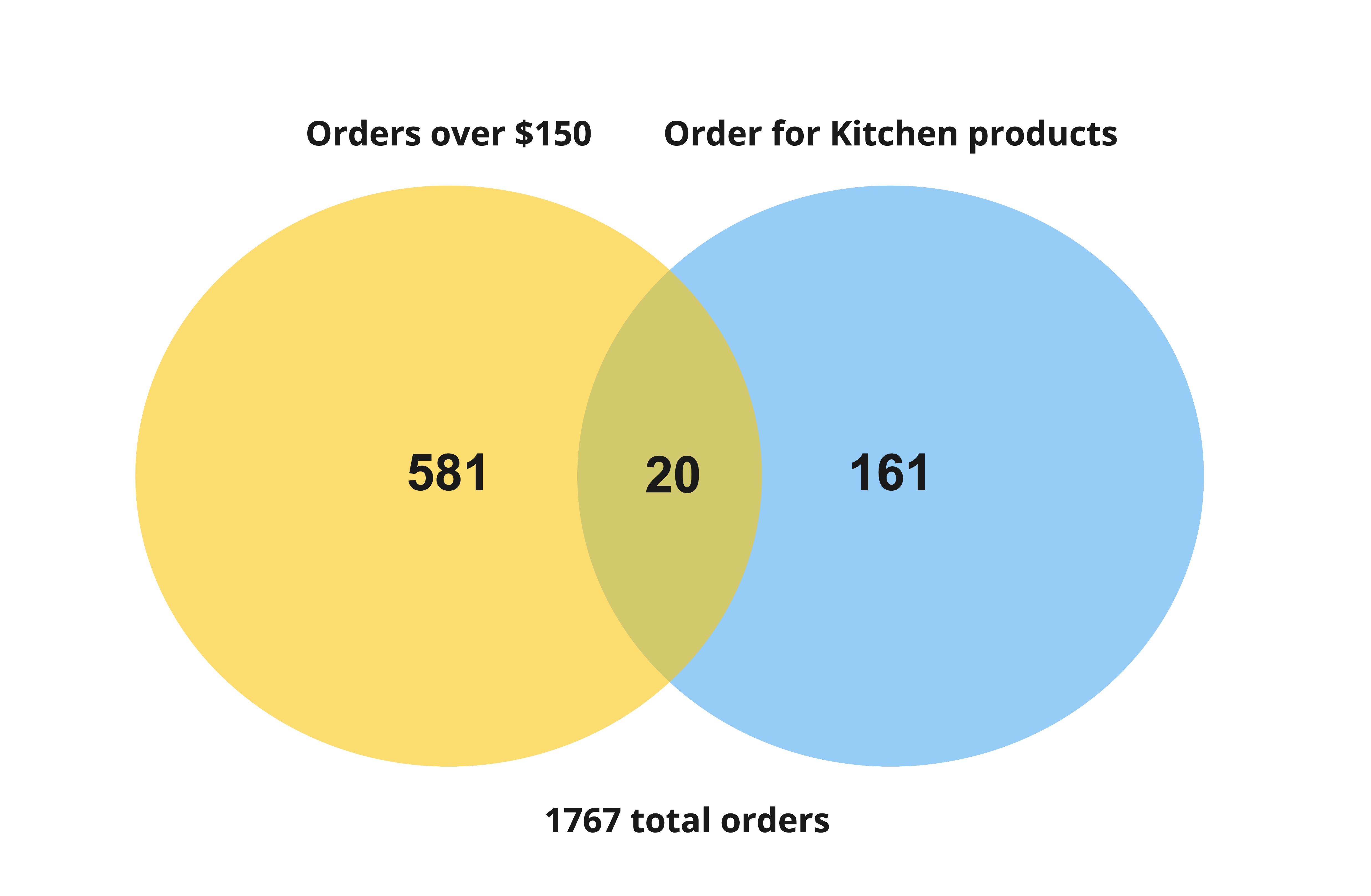
$$P(Pedido cocina > 150 |) = \frac{\frac{20}{1767}}{\frac{601}{1767}}$$
$$P(Pedido cocina > 150 |) = \frac{20}{601} $$
Fórmula de probabilidad condicional
$$P(A | B) = \frac{{P(A \ \cap \ B)}}{{P(B)}}$$
$P(A | B)$ → Probabilidad del suceso A, dado el evento B
$P(A \ \cap \ B)$ → Probabilidad de que ocurran el suceso A y el suceso B
- Dividido por la probabilidad del suceso B → $P(B)$
¡Vamos a practicar!
Introducción a la estadística

