Medidas de dispersión

Introducción a la estadística

George Boorman

Curriculum Manager, DataCamp

¿Qué es la dispersión?

vehicle_crimes_histogram_with_wide_spread.png

burlgary_crimes_histogram_with_narrow_spread.png

Introducción a la estadística

¿Por qué es importante la dispersión?

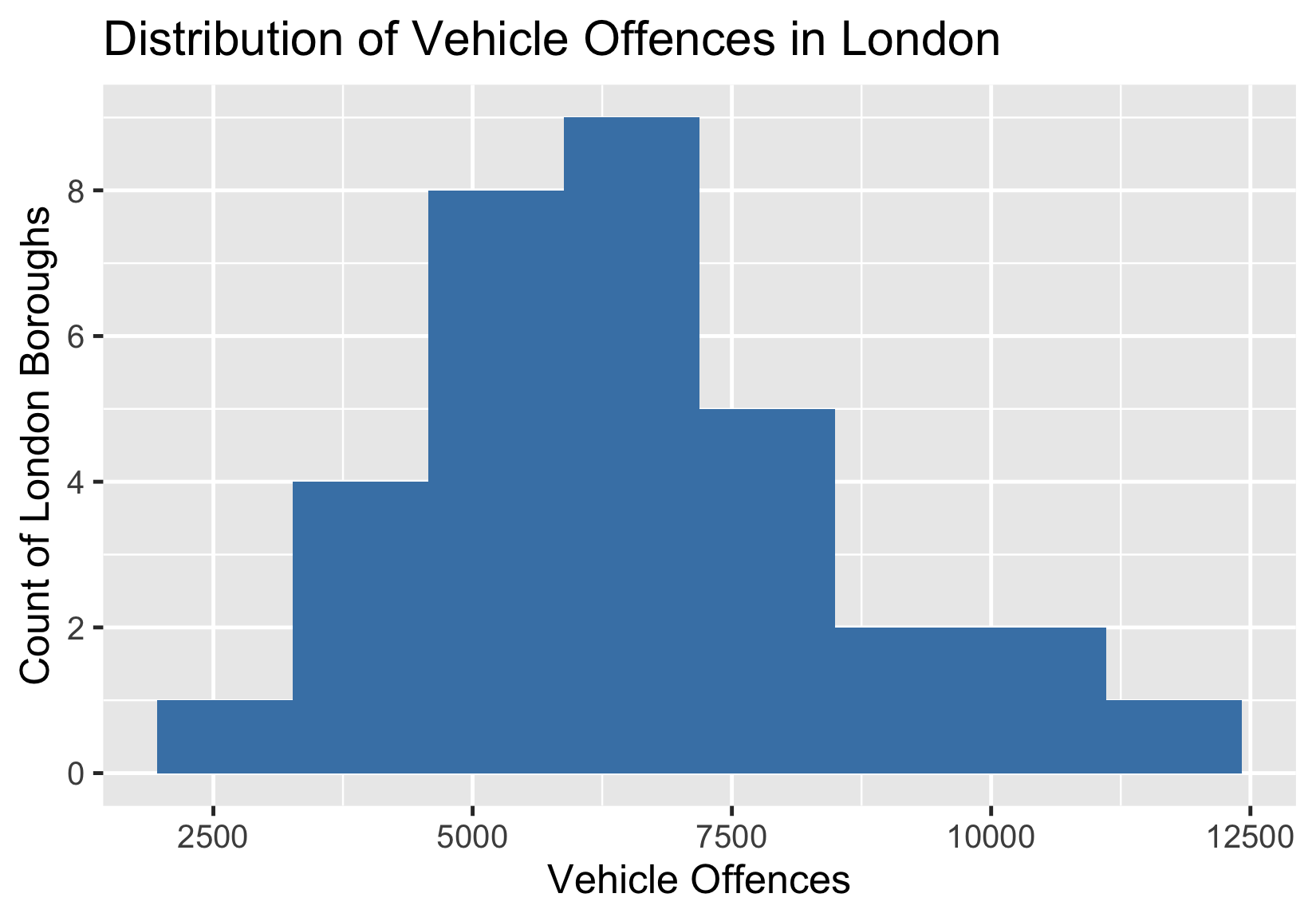
  • La dispersión mide la variedad de los datos.

 

  • Las camisetas suelen costar 30 USD

    • El coste puede estar entre 10 y 200 USD.
    • ¿Qué probabilidad hay de que una cueste 30 USD?

  • Si las camisetas costaran entre 20 y 50 USD:

    • ¿Cambia esto la probabilidad de encontrar una por 30 USD?

t_shirt_hanging_against_a_wall.jpg

1 Crédito de la imagen: https://unsplash.com/@uyk
Introducción a la estadística

Rango

 

${rango} = máximo - mínimo$

 

${rango(Robos)} = 5183 - 1432$

${rango(Robos)} = 3751$

Municipio Robo con allanamiento de morada
Tower Hamlets 5183
Hackney 5079
Barnet 5067
... ...
Sutton 1815
Bexley 1583
Kingston upon Thames 1432
Introducción a la estadística

Varianza

Un gráfico de puntos de 75 puntos de datos con una línea roja en el centro que representa la media

Introducción a la estadística

Varianza

variance_plot_showing_distance_between_Westminster_and_the_mean.png

Introducción a la estadística

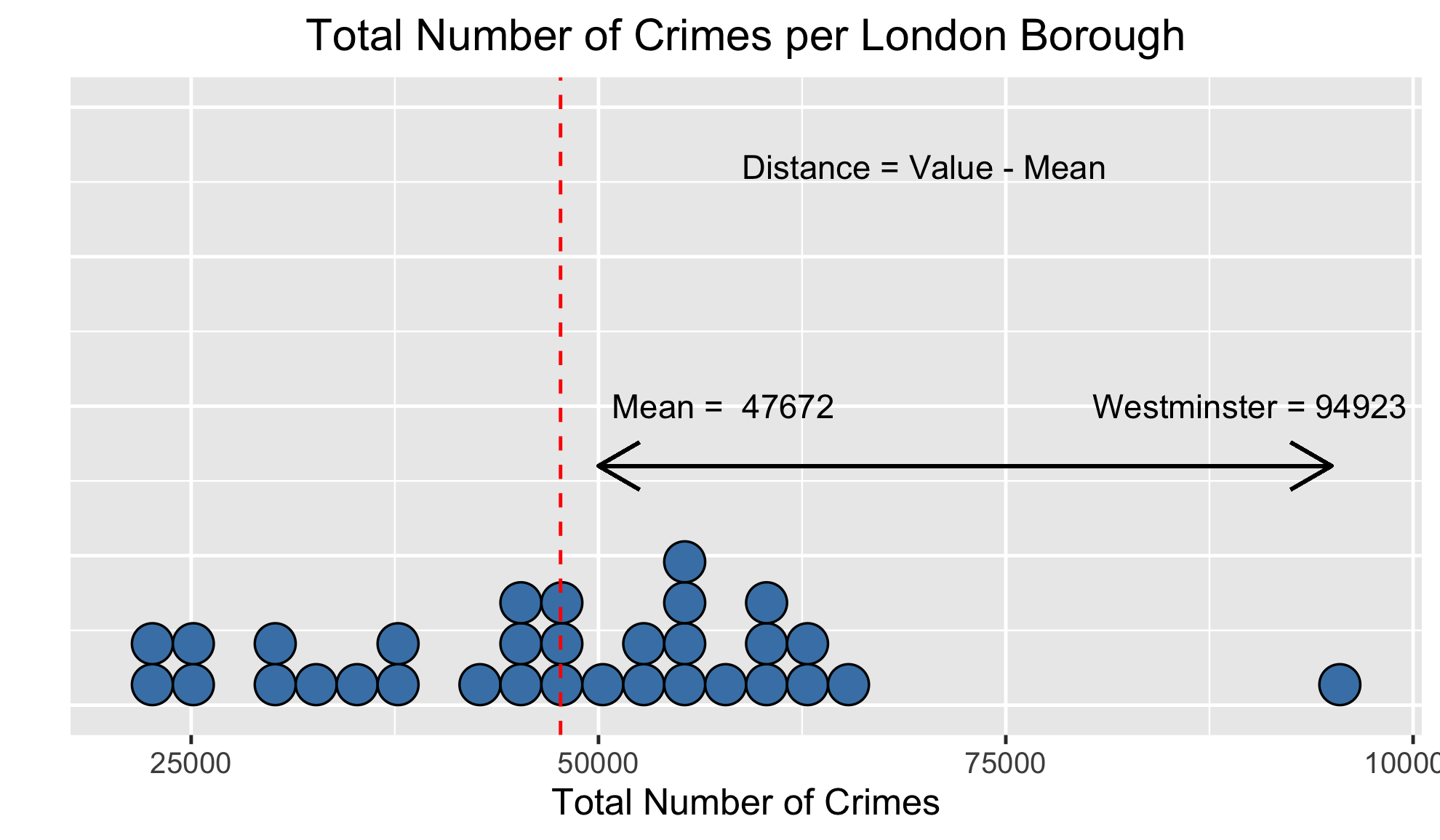
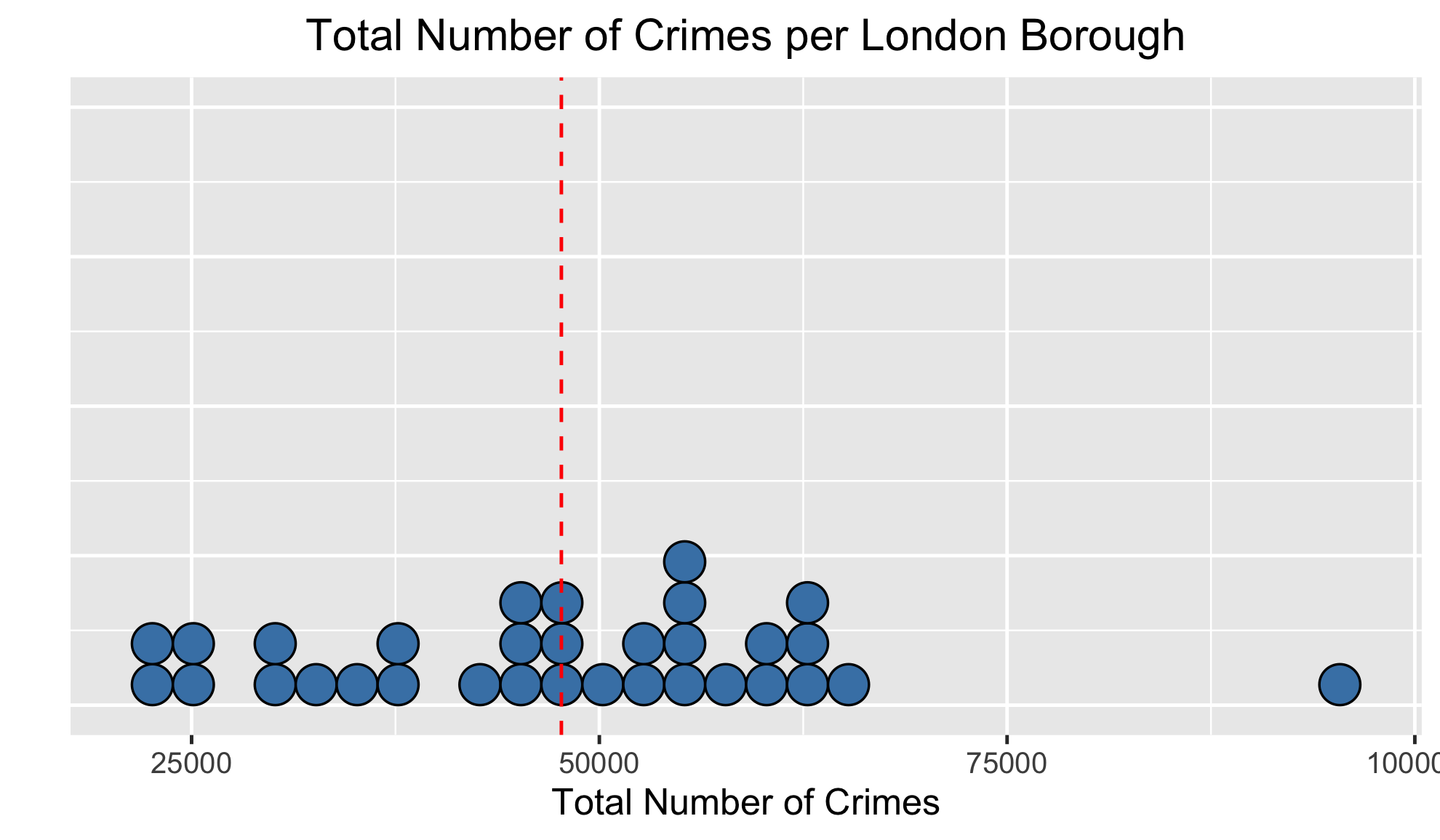
Varianza

Municipio Delitos totales Media Distancia
Barking y Dagenham 37 939 47 672 -9733
Barnet 52 421 47 672 4749
Bexley 29 285 47 672 -18 387
Brent 55 465 47 672 7793
Bromley 42 982 47 672 4690
Camden 54 806 47 672 7134
... ... ... ...
Total 1 525 492 1 525 492 0
Introducción a la estadística

Varianza

Municipio Delitos totales Media Distancia Distancia al cuadrado
Barking y Dagenham 37 939 47 672 -9733 94 731 289
Barnet 52 421 47 672 4749 22 553 001
Bexley 29 285 47 672 -18 387 338 081 769
Brent 55 465 47 672 7793 60 730 849
Bromley 42 982 47 672 4690 21 996 100
Camden 54 806 47 672 7134 50 893 956
... ... ... ... ...
Total 1 525 492 1 525 492 0 7 509 750 824
Introducción a la estadística

Varianza

 

$${varianza(total \ delitos)} = \frac{7 509 750 824}{32}$$

$${varianza(total \ delitos)} = \ 234 679 713$$

Introducción a la estadística

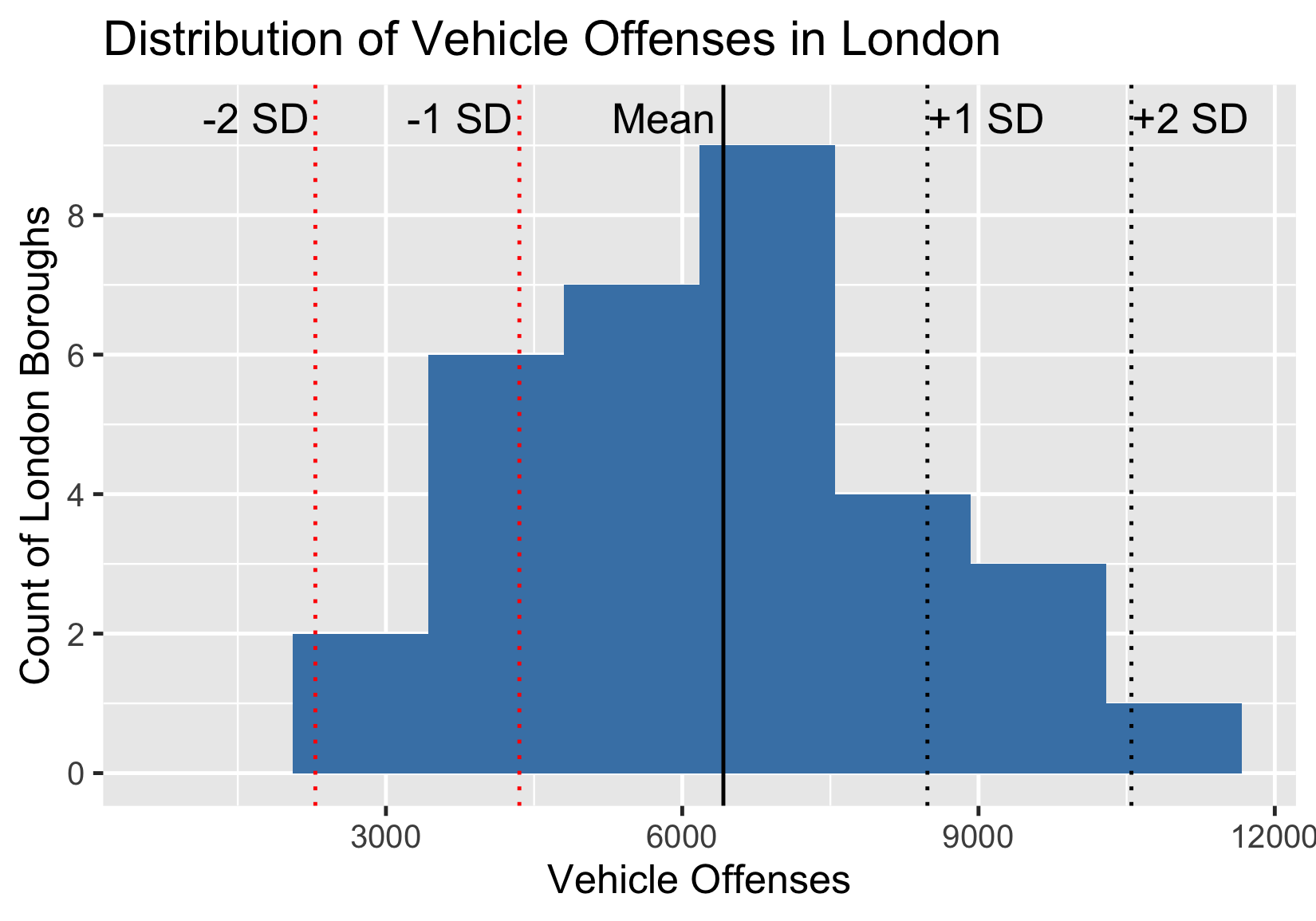
Desviación típica

${desviación \ típica(total \ delitos)} = {\sqrt( varianza(total \ delitos))}$

${desviación \ típica(total \ delitos)} = {\sqrt(234 679 713)}$

${desviación \ típica(total \ delitos)} = 15 319,26$

  • Desviación típica cercana a cero = datos agrupados alrededor de la media
Introducción a la estadística

Desviación típica en un histograma

vehicle_crime_histogram_with_one_and_two_standard_deviations_from_the_mean.png

Introducción a la estadística

Cuartiles

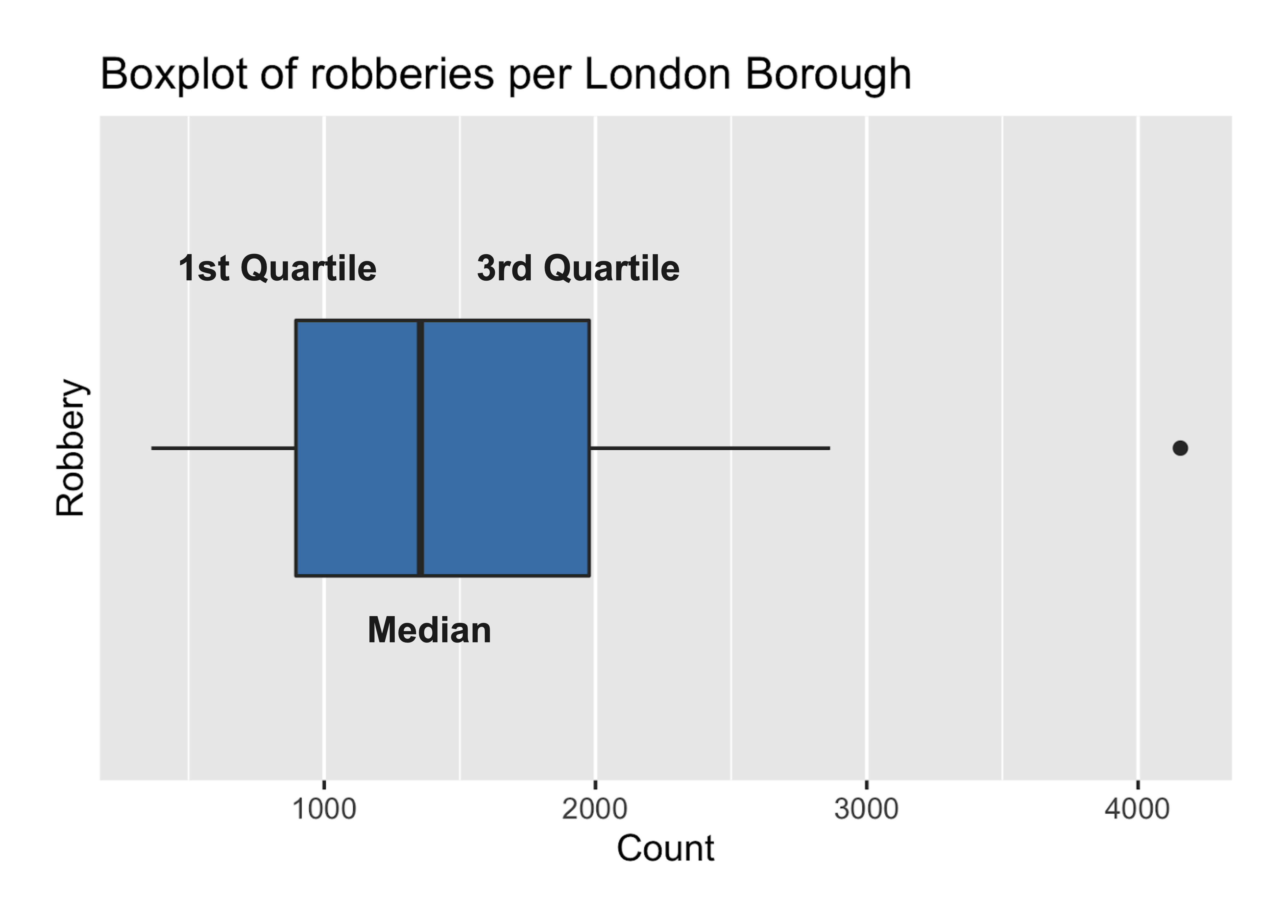
  • Cuartiles:
    • Se dividen los datos en cuatro partes iguales.

 

Delito 0 % 25 % 50 % 75 % 100 %
Robo con allanamiento de morada 1432,00 2681,75 3416,50 4392,00 5183,00
Asalto 363,00 895,75 1354,50 1976,50 4156,00
Robo 4090,00 7739,75 9624,00 12 059,00 40 278,00
Infracciones de tráfico 2143,00 4838,25 6424,50 7520,75 11 292,00
Introducción a la estadística

Cuartiles

  • Cuartiles:
    • Se dividen los datos en cuatro partes iguales.

 

Delito 0 % 25 % 50 % 75 % 100 %
Robo con allanamiento de morada 1432,00 2681,75 3416,50 4392,00 5183,00
Asalto 363,00 895,75 1354,50 1976,50 4156,00
Robo 4090,00 7739,75 9624,00 12 059,00 40 278,00
Infracciones de tráfico 2143,00 4838,25 6424,50 7520,75 11 292,00

 

  • Segundo cuartil (50 %) = mediana
Introducción a la estadística

Diagramas de caja

boxplot_of_robberies_in_London_with_median_plus_first_and_third_quartiles_highlighted.png

Introducción a la estadística

Intervalo intercuartílico (IQR)

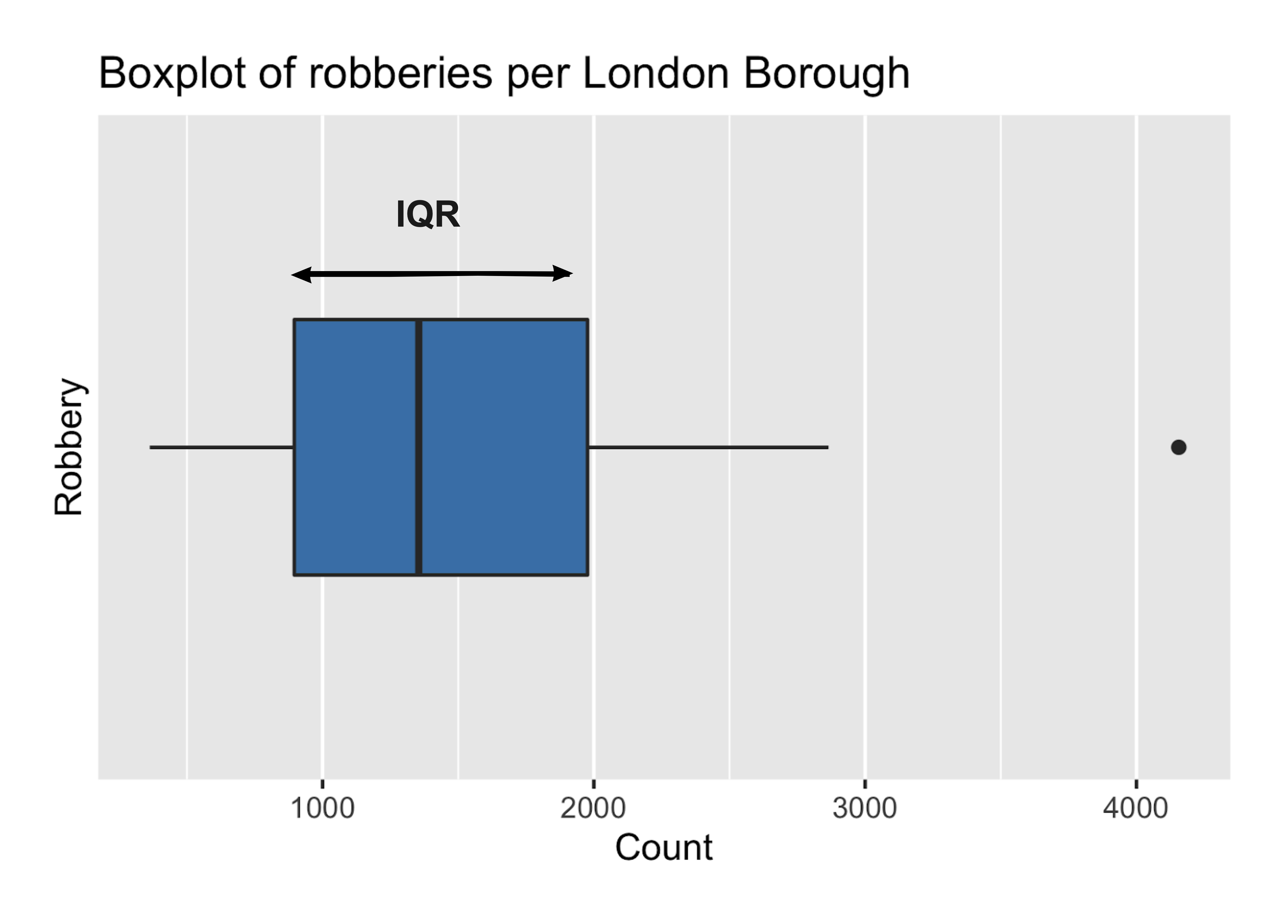
boxplot_robberies_in_London_with_interquartile_range_highlighted.png

  • El IQR se ve menos afectado por los valores extremos

          IQR = tercer cuartil - primer cuartil

                IQR = 1976,50 - 895,75

                       IQR = 1080,75

Introducción a la estadística

¡Vamos a practicar!

Introducción a la estadística

Preparing Video For Download...