¿Qué probabilidad hay?

Introducción a la estadística

George Boorman

Curriculum Manager, DataCamp

Medir la probabilidad

¿Cuál es la probabilidad de un suceso?

$$ P(\text{event}) = \frac{\text{\# ways event can happen}}{\text{total \# of possible outcomes}} $$

Ejemplo: lanzar una moneda

$$ P(\text{heads}) = \frac{\text{1 way to get heads}}{\text{2 possible outcomes}} = \frac{1}{2} = 50\%$$

line of probability from left where 0 percent = impossible, to right where 100 percent = will certainly happen.png

Box with Amir, Brian, Claire, and Damian's names.png

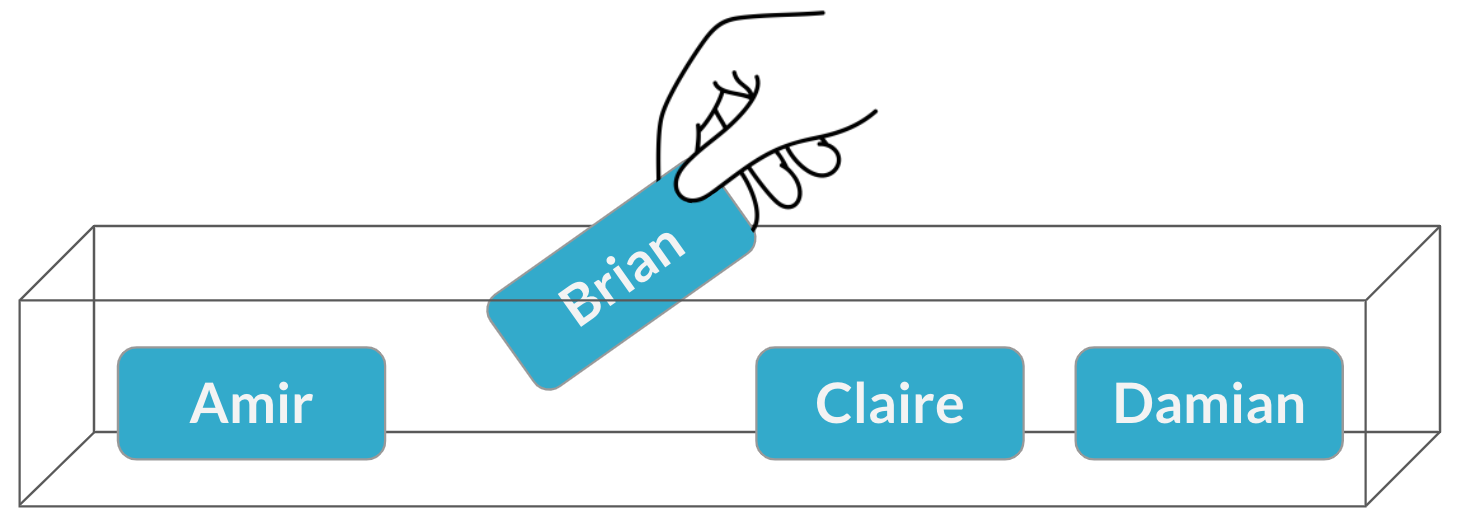
Pulling out Brian's name from the box.png

$$P(\text{Brian}) = \frac{1}{4} = 25\%$$

Pulling out Brian's name from the box.png

Pulling out Brian's name from the box.png

$$P(\text{Brian}) = \frac{1}{4} = 25\%$$

Dos sucesos son independientes si la probabilidad del segundo evento no cambia en función del resultado del primero.

Número de pedido	Tipo de producto	Cantidad neta	Ventas brutas	Descuentos	Devoluciones	Ventas netas
200	Cesta	13	3744,0	-316,80	0,00	3427,20
201	Cesta	12	3825,0	-201,60	-288,0	3335,40
202	Cesta	17	3035,0	-63,25	0,00	2971,75
203	Arte y escultura	47	2696,8	-44,16	0,00	2652,64
204	Cesta	17	2695,0	-52,50	-110,00	2532,50

¹ Crédito de la imagen: https://unsplash.com/@rodriguezedm

$$P(Joyería) = \frac{Número \ pedido(Joyería)}{Sum(Total \ número \ pedidos)}$$

$$P(Joyería) = \frac{210}{1767}$$

$$P(Joyería) = 11,88 %$$

Introducción a la estadística