Correlation caveats
Introduction to Statistics in R

Maggie Matsui
Content Developer, DataCamp
Non-linear relationships
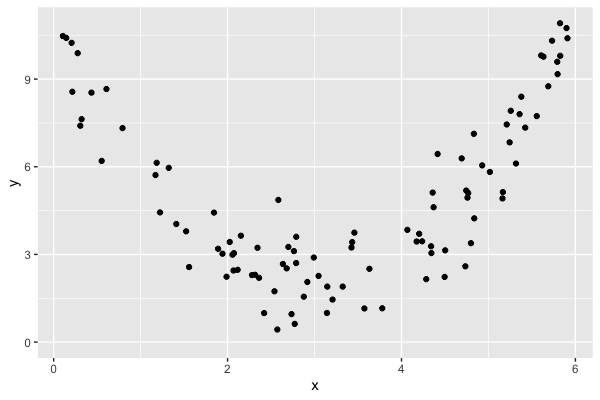
$$r = 0.18$$
Non-linear relationships
What we see:
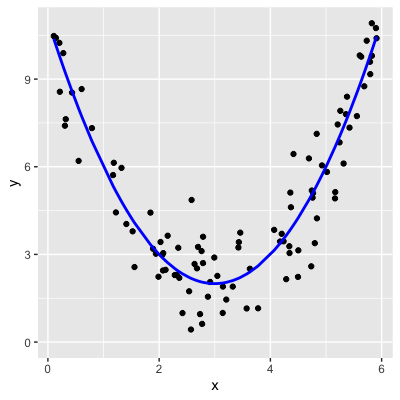
What the correlation coefficient sees:
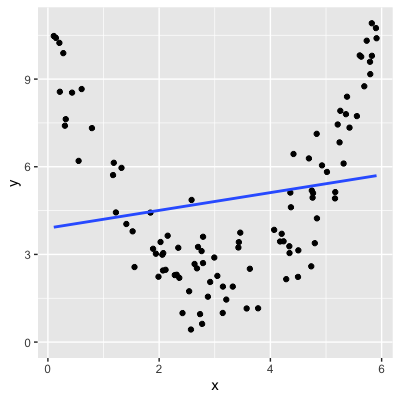
Correlation only accounts for linear relationships
Correlation shouldn't be used blindly
cor(df$x, df$y)
0.1786163
Always visualize your data

Mammal sleep data
msleep
name vore sleep_total awake bodywt
1 Cheetah carni 12.1 11.9 50
2 Owl monkey omni 17 7 0.48
3 Mountain beaver herbi 14.4 9.6 1.35
4 Greater short-tailed shrew omni 14.9 9.1 0.019
5 Cow herbi 4 20 600
6 Three-toed sloth herbi 14.4 9.6 3.85
...
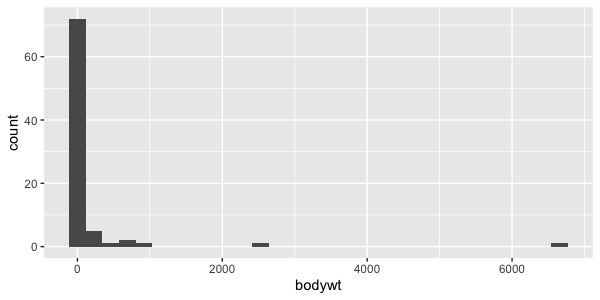
Body weight vs. awake time
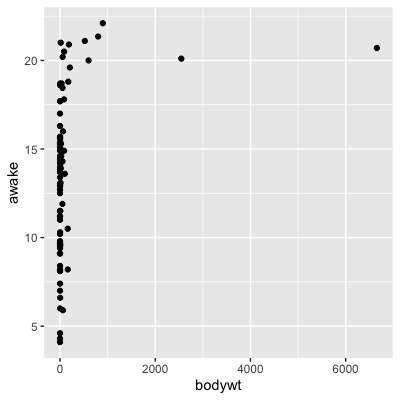
cor(msleep$bodywt, msleep$awake)
0.3119801
Distribution of body weight
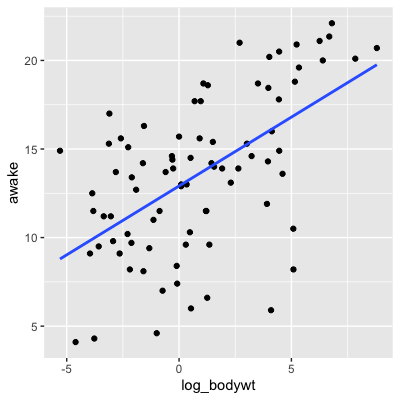
Log transformation
msleep %>% mutate(log_bodywt = log(bodywt)) %>%ggplot(aes(log_bodywt, awake)) + geom_point() + geom_smooth(method = "lm", se = FALSE)
cor(msleep$log_bodywt, msleep$awake)
0.5687943
Other transformations
- Log transformation (
log(x)) - Square root transformation (
sqrt(x)) Reciprocal transformation (
1 / x)Combinations of these, e.g.:
log(x)andlog(y)sqrt(x)and1 / y
Why use a transformation?
- Certain statistical methods rely on variables having a linear relationship
- Correlation coefficient
- Linear regression
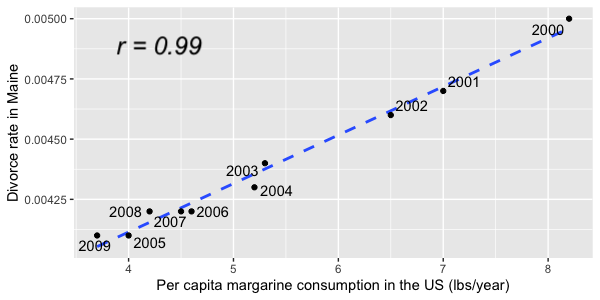
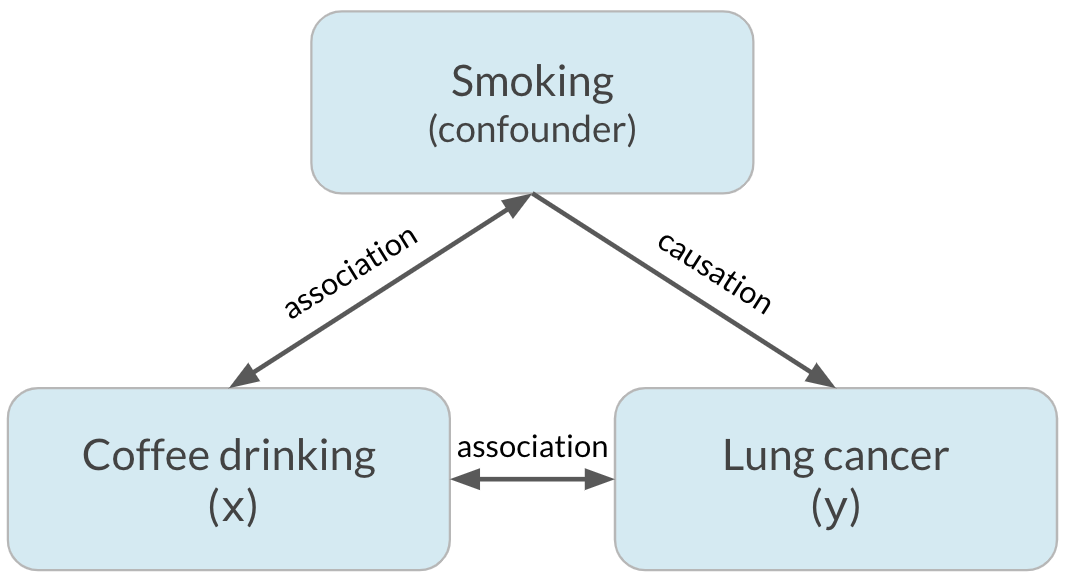
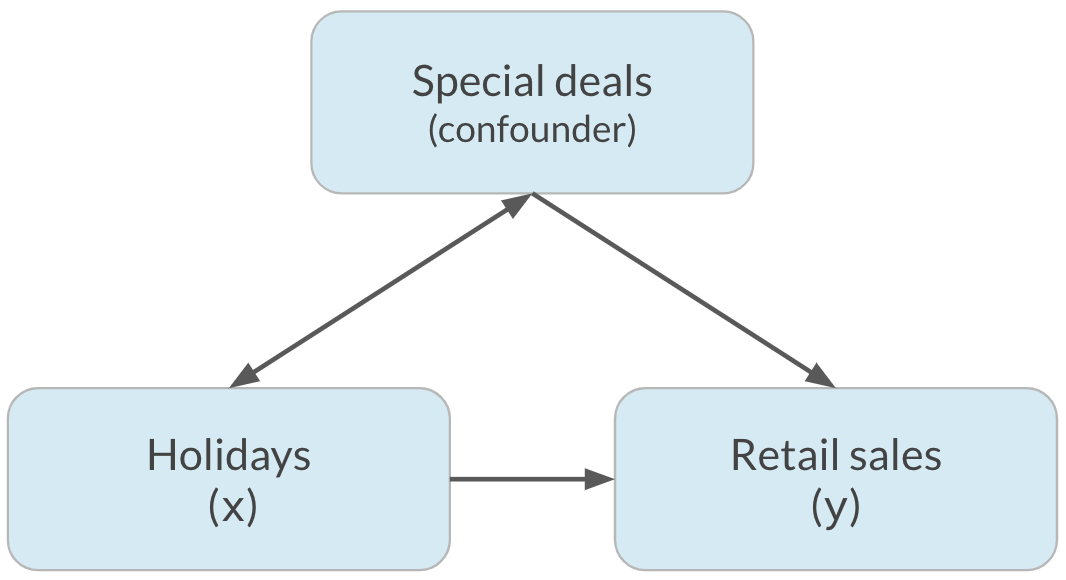
Correlation does not imply causation
x is correlated with y does not mean x causes y
Confounding
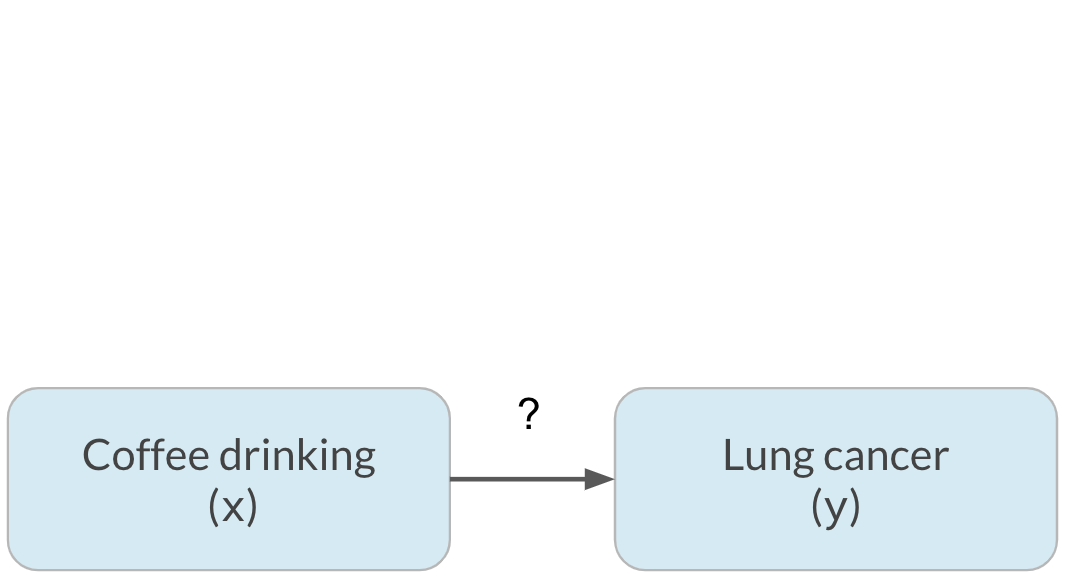
Confounding
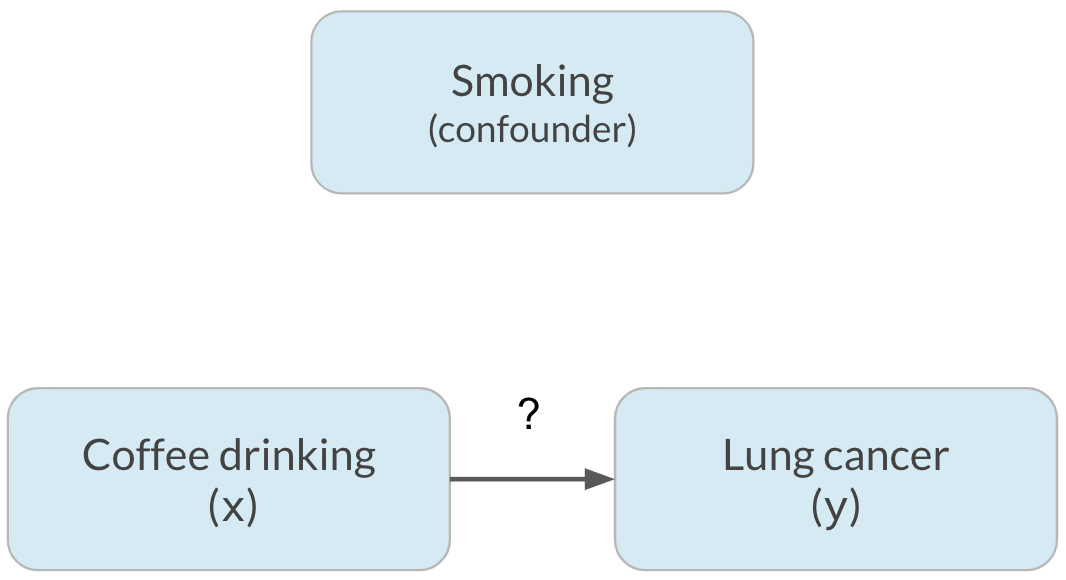
Confounding
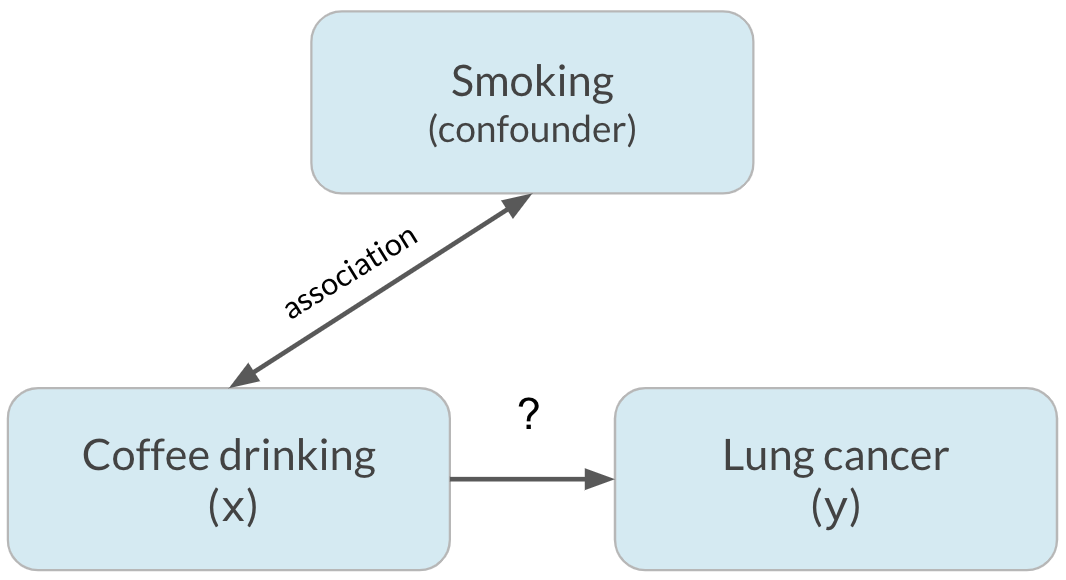
Confounding
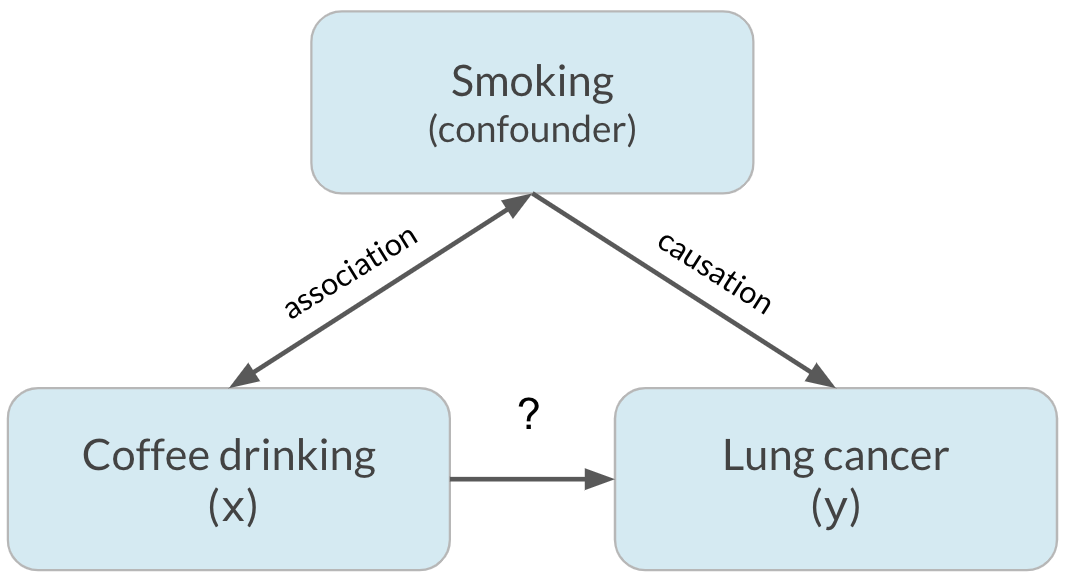
Confounding
Let's practice!
Introduction to Statistics in R

