Descubrir las funciones de activación

Introducción al aprendizaje profundo con PyTorch

Jasmin Ludolf

Senior Data Science Content Developer, DataCamp

Funciones de activación

Las funciones de activación añaden no linealidad a la red
- Sigmoide para clasificación binaria
- Softmax para clasificación multiclase
Una red puede aprender relaciones más complejas con no linealidad
Salida de "preactivación" pasada a la función de activación

Diagrama de una red neuronal con capas lineales y una función de activación

Descubre la función sigmoide

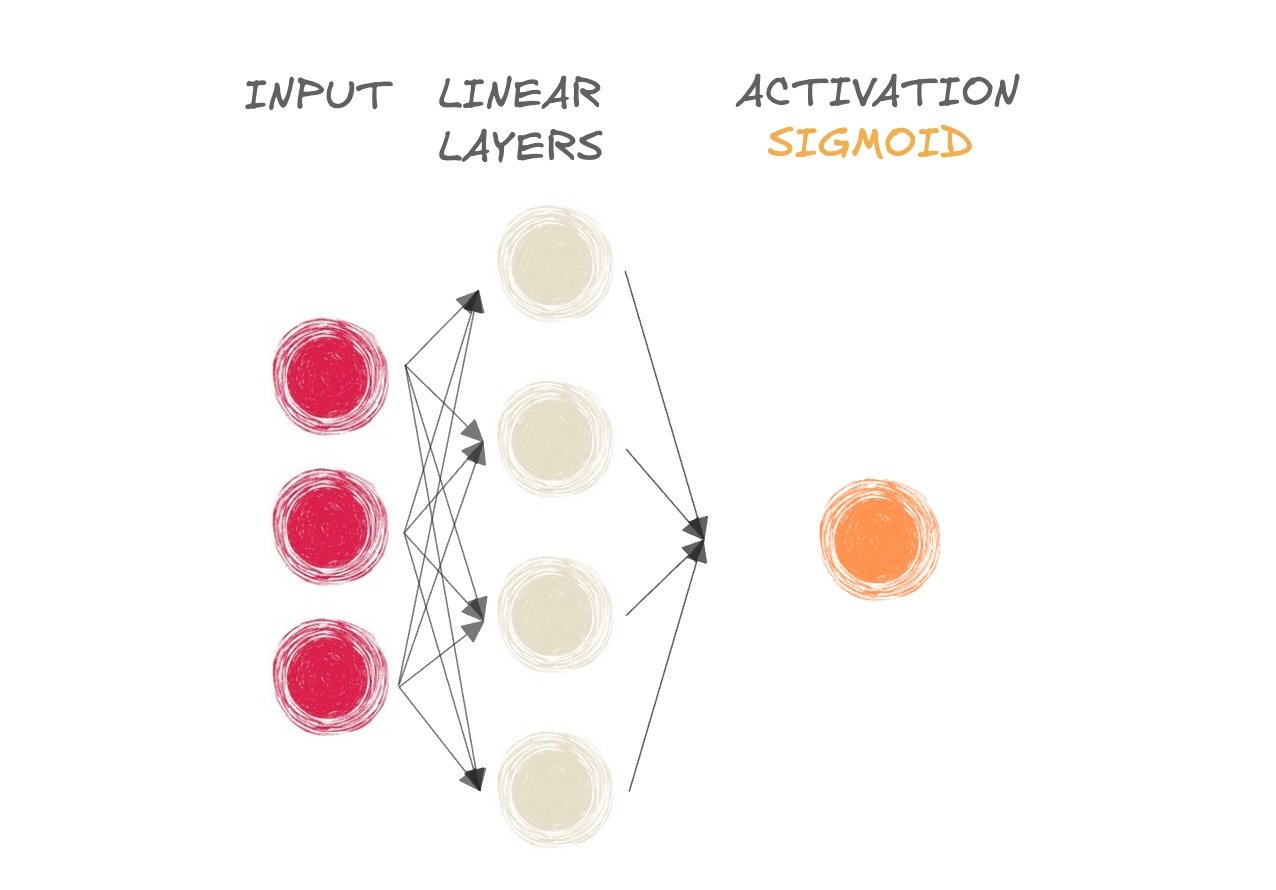
Diagrama de parte de una red neuronal con entrada, capas lineales y función de activación

¿Mamífero o no?

Una ilustración de un lémur

Descubre la función sigmoide

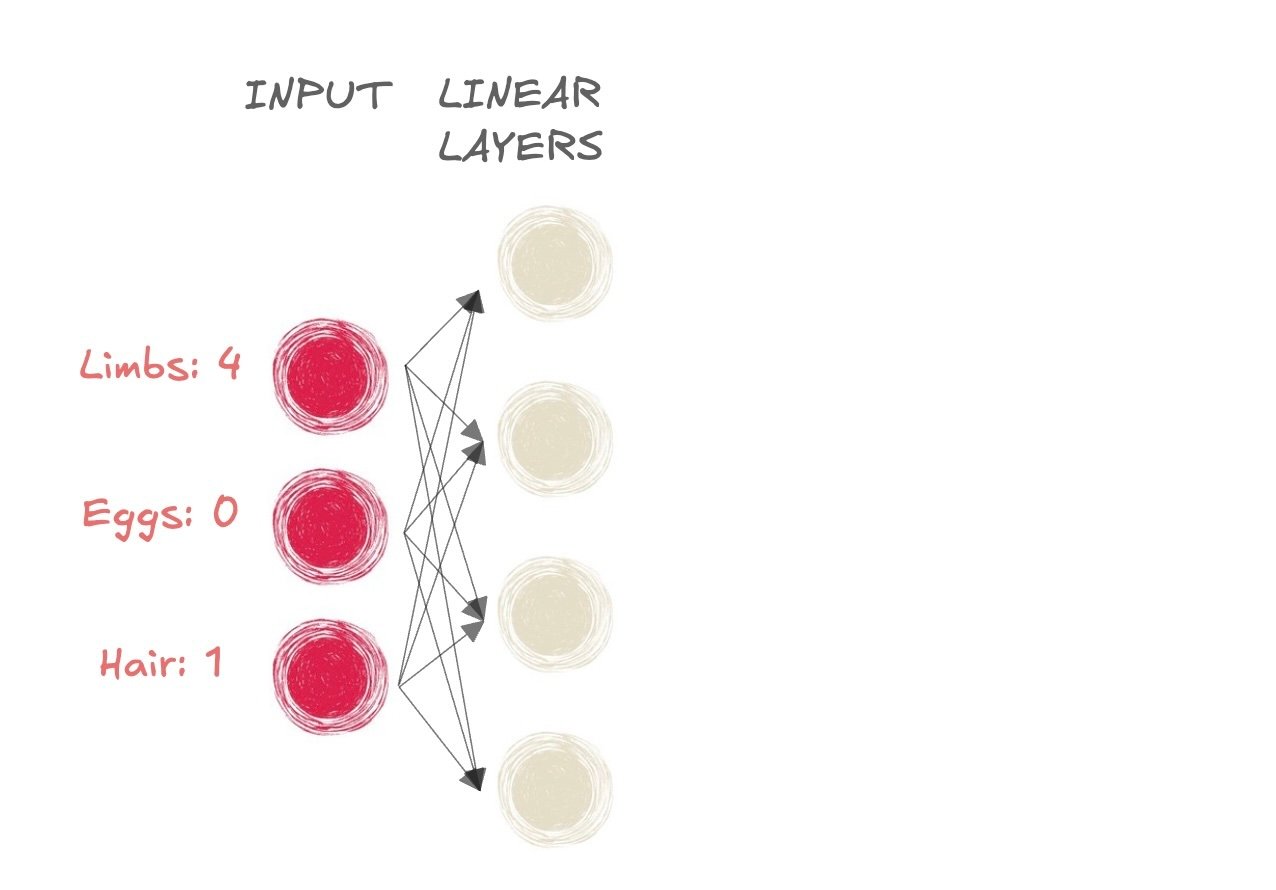
Diagrama de parte de una red neuronal con entradas y capas lineales

¿Mamífero o no?

Una ilustración de un lémur

Entrada:
- Extremidades: 4
- Huevos: 0
- Pelo: 1

Descubre la función sigmoide

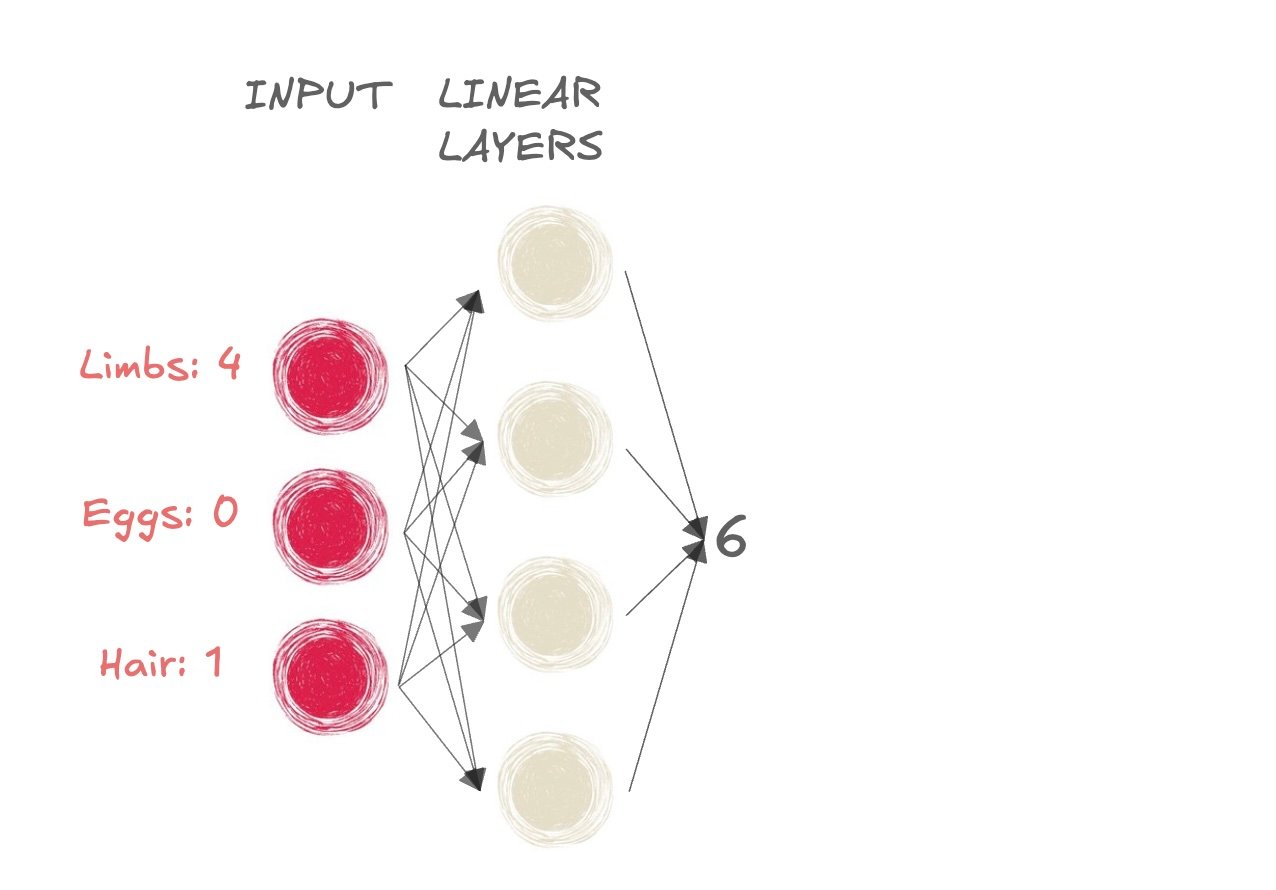
Diagrama de parte de una red neuronal con entradas y el número 6 como salida a las capas lineales

¿Mamífero o no?

Una ilustración de un lémur

La salida a las capas lineales es 6

Descubre la función sigmoide

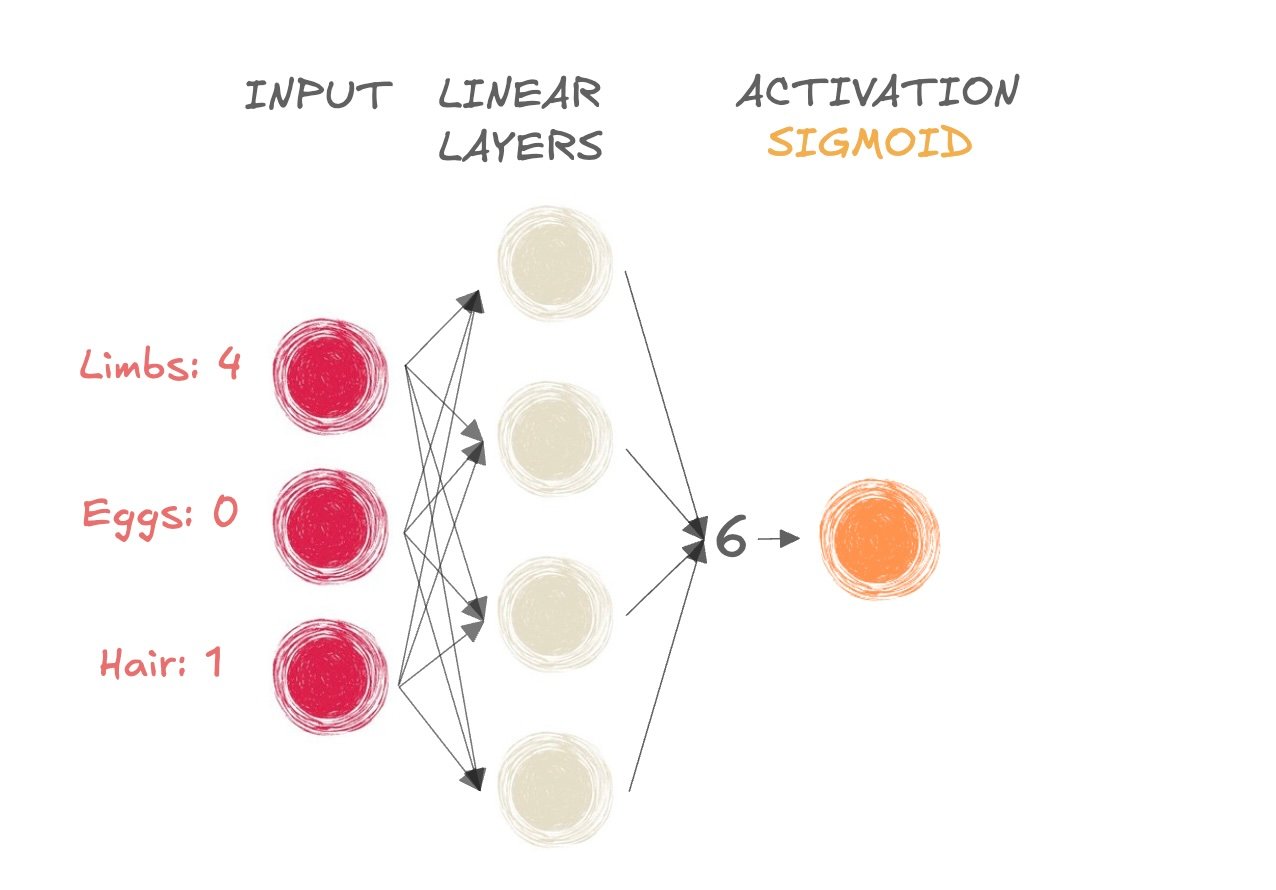
Diagrama de parte de una red neuronal con entradas, el número 6 como salida a las capas lineales y una función de activación sigmoide

¿Mamífero o no?

Una ilustración de un lémur

Tomamos la salida de la preactivación (6) y la pasamos a la función sigmoide

Descubre la función sigmoide

Diagrama de parte de una red neuronal con entradas, el número 6 como salida a las capas lineales, una función de activación sigmoide y una salida

¿Mamífero o no?

Una ilustración de un lémur

Tomamos la salida de la preactivación (6) y la pasamos a la función sigmoide
Obtener un valor entre 0 y 1
Si el resultado es > 0,5, etiqueta de clase = 1 (mamífero)
Si el resultado es <= 0,5, etiqueta de clase = 0 (no mamífero)

Descubre la función sigmoide

import torch
import torch.nn as nn

input_tensor = torch.tensor([[6]])
sigmoid = nn.Sigmoid()

output = sigmoid(input_tensor)
print(output)

tensor([[0.9975]])

Activación como última capa

model = nn.Sequential(
  nn.Linear(6, 4), # First linear layer
  nn.Linear(4, 1), # Second linear layer
  nn.Sigmoid() # Sigmoid activation function
)

La sigmoide como último paso en la red de capas lineales es equivalente a la regresión logística tradicional

Familiarizarse con softmax

Tres clases:

Familiarizarse con softmax

Tres clases:

Un lémur con la opción ave

Familiarizarse con softmax

Tres clases:

Un lémur con las opciones ave y mamífero

Familiarizarse con softmax

Tres clases:

Un lémur con tres opciones: ave, mamífero o reptil

Familiarizarse con softmax

Diagrama de parte de una red neuronal con entradas

Toma tres dimensiones como entrada y da como salida la misma forma

Familiarizarse con softmax

Diagrama de parte de una red neuronal con entradas, un vector como salida a las capas lineales, una función de activación softmax y una salida

Toma tres dimensiones como entrada y da como salida la misma forma
Produce una distribución de probabilidad:
- Cada elemento es una probabilidad (está acotada entre 0 y 1)
- La suma del vector de salida es igual a 1

Familiarizarse con softmax

Diagrama de parte de una red neuronal con entradas, un vector como salida a las capas lineales, una función de activación softmax y una salida

Toma tres dimensiones como entrada y da como salida la misma forma
Produce una distribución de probabilidad:
- Cada elemento es una probabilidad (está acotada entre 0 y 1)
- La suma del vector de salida es igual a 1

Familiarizarse con softmax

import torch
import torch.nn as nn

# Create an input tensor
input_tensor = torch.tensor(
    [[4.3, 6.1, 2.3]])

# Apply softmax along the last dimension

probabilities = nn.Softmax(dim=-1)
output_tensor = probabilities(input_tensor)
print(output_tensor)

tensor([[0.1392, 0.8420, 0.0188]])

dim = -1 indica que se aplica softmax a la última dimensión del tensor de entrada
nn.Softmax() puede utilizarse como último paso en nn.Sequential()

¡Vamos a practicar!

Introducción al aprendizaje profundo con PyTorch