Noções básicas de regressão linear

Aprendizado Supervisionado com o scikit-learn

George Boorman

Core Curriculum Manager, DataCamp

Como funciona a regressão

$y = ax + b$
- A regressão linear simples usa uma única variável independente
  - $y$ = variável dependente
  - $x$ = apenas uma variável independente
  - $a$, $b$ = parâmetros/coeficientes do modelo – inclinação, intercepto
Como escolher $a$ e $b$?
- Definir uma função de erro para uma determinada linha
- Escolher a linha que minimiza a função de erro
Função de erro = função de perda = função de custo

A função de perda

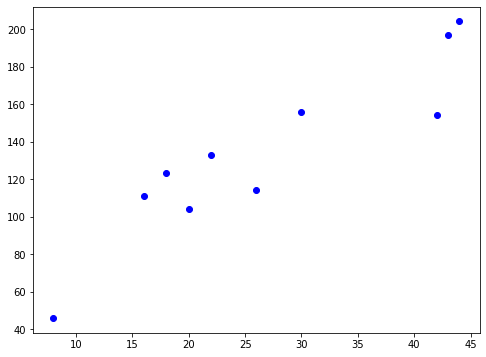
gráfico de dispersão

A função de perda

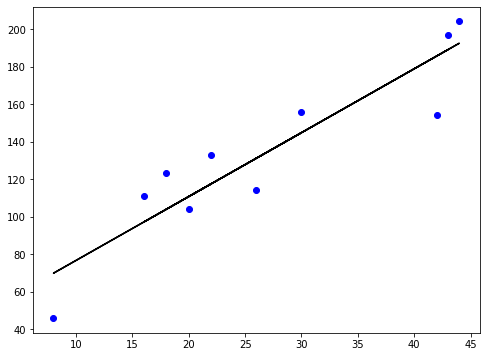
linha de regressão que vai do canto inferior esquerdo ao canto superior direito, passando pelo meio das observações

A função de perda

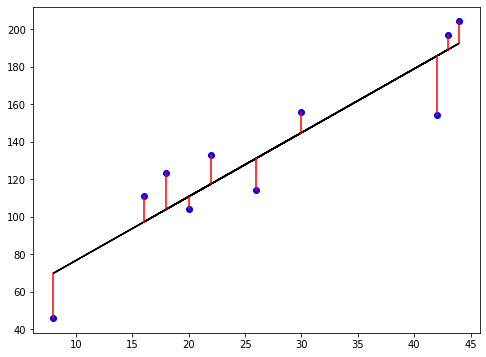
linhas vermelhas ligadas à linha de regressão para cada observação

A função de perda

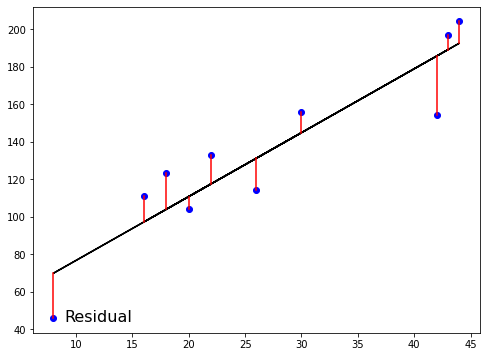
as linhas vermelhas representam os resíduos

A função de perda

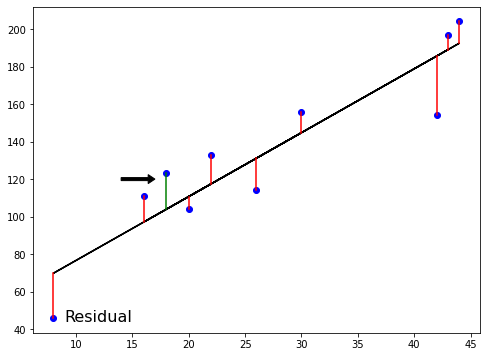
seta destacando um resíduo positivo, pois a observação está acima da linha de regressão

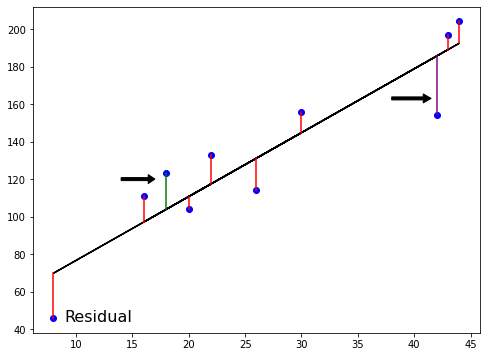
Método dos Mínimos Quadrados

a segunda seta aponta para um resíduo abaixo da linha de regressão, representando um resíduo negativo

$RSS = $ $\displaystyle\sum_{i=1}^{n}(y_i-\hat{y_i})^2$

Método dos Mínimos Quadrados (MMQ): minimiza a SQR (RSS, em inglês)

Regressão linear com mais dimensões

$$ y = a_{1}x_{1} + a_{2}x_{2} + b$$

Para ajustar um modelo de regressão linear aqui:
- É preciso especificar 3 variáveis: $ a_1,\ a_2,\ b $
Com mais dimensões:
- Conhecida como regressão múltipla
- É preciso especificar os coeficientes de cada variável independente e a variável $b$

$$ y = a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3} +... + a_{n}x_{n}+ b$$

O scikit-learn funciona exatamente da mesma forma:
- Passe duas matrizes: variáveis independentes e variável dependente

Regressão linear usando todas as variáveis independentes

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
                                                    random_state=42)

reg_all = LinearRegression()

reg_all.fit(X_train, y_train)

y_pred = reg_all.predict(X_test)

R-quadrado

$R^2$: quantifica a variância nos valores da variável dependente explicada pelas variáveis independentes
- Os valores variam de 0 a 1
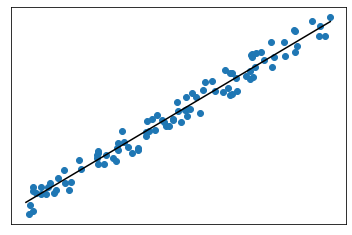
$R^2$ alto:

linha de regressão a 45 graus que vai do canto inferior esquerdo ao canto superior direito e passa perto de todas as observações

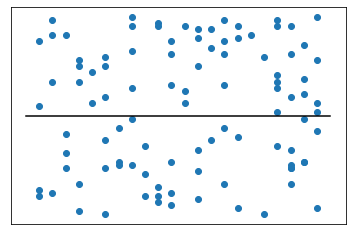
$R^2$ baixo:

linha de regressão que segue na horizontal, com observações dispersas e longe da linha

R-quadrado no scikit-learn

reg_all.score(X_test, y_test)

0.356302876407827

Erro quadrático médio e raiz do erro quadrático médio

$MSE = $ $\displaystyle\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y_i})^2$

O $MSE$ é medido em unidades da variável dependente ao quadrado

$RMSE = $ $\sqrt{MSE}$

Meça o $RMSE$ nas mesmas unidades da variável dependente

RMSE no scikit-learn

from sklearn.metrics import root_mean_squared_error


root_mean_squared_error(y_test, y_pred)

24.028109426907236

Vamos praticar!

Aprendizado Supervisionado com o scikit-learn