Tratamento de valores discrepantes

Análise Exploratória de Dados em Python

George Boorman

Curriculum Manager, DataCamp

O que é uma discrepância?

Uma observação bem diferente dos outros dados
- Preço médio das casas: US$ 400.000
- Preço atípico da casa: US$ 5.000.000

Considerar por que o valor é diferente:
- Localização, número de quartos, tamanho total, etc.

Casa grande com piscina

¹ Crédito da imagem: https://unsplash.com/@ralphkayden

Usar estatísticas descritivas

print(salaries["Salary_USD"].describe())

count       518.000
mean     104905.826
std       62660.107
min        3819.000
25%       61191.000
50%       95483.000
75%      137496.000
max      429675.000
Name: Salary_USD, dtype: float64

Usar o intervalo interquartil

Intervalo interquartil (IQR)

IQR = percentil 75 - percentil 25

IQR em diagramas de caixa

sns.boxplot(data=salaries,
            y="Salary_USD")
plt.show()

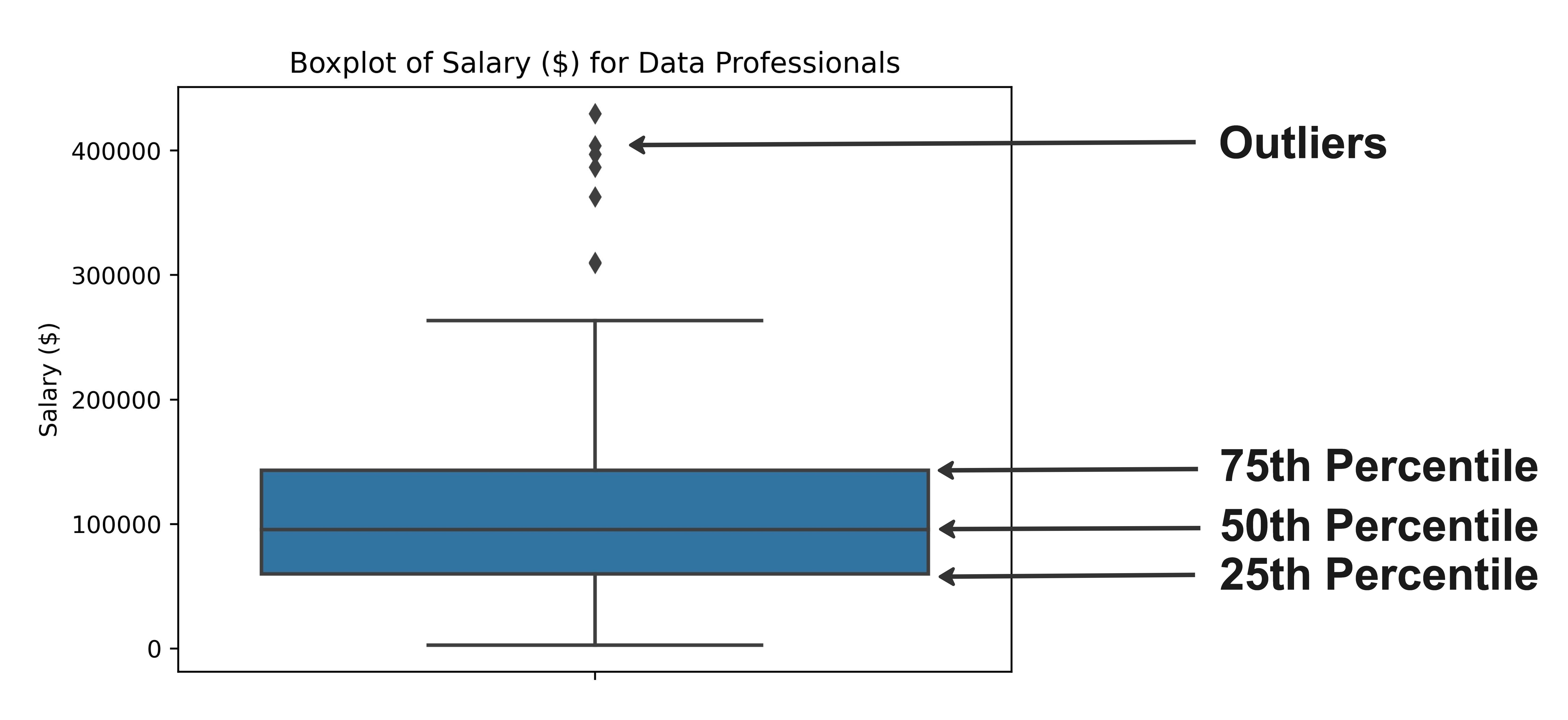
Gráfico de caixa dos salários dos profissionais de dados, mostrando o percentil 25 na parte inferior da caixa, o percentil 50 como linha média, o percentil 75 na parte superior da caixa e os outliers como diamantes fora da caixa

Usar o intervalo interquartil

Intervalo interquartil (IQR)

IQR = percentil 75 - percentil 25
Discrepâncias superiores > 75º percentil + (1,5 * IQR)
Discrepâncias inferiores < 25º percentil - (1,5 * IQR)

Identificar limites

# 75th percentile
seventy_fifth = salaries["Salary_USD"].quantile(0.75)


# 25th percentile
twenty_fifth = salaries["Salary_USD"].quantile(0.25)


# Interquartile range
salaries_iqr = seventy_fifth - twenty_fifth


print(salaries_iqr)

76305.0

Identificação de valores discrepantes

# Upper threshold
upper = seventy_fifth + (1.5 * salaries_iqr)


# Lower threshold
lower = twenty_fifth - (1.5 * salaries_iqr)


print(upper, lower)

251953.5 -53266.5

Criar subconjunto dos dados

salaries[(salaries["Salary_USD"] < lower) | (salaries["Salary_USD"] > upper)] \

        [["Experience", "Employee_Location", "Salary_USD"]]

        Experience    Employee_Location    Salary_USD
29      Mid           US                   429675.0
67      Mid           US                   257805.0
80      Senior        US                   263534.0
83      Mid           US                   429675.0
133     Mid           US                   403895.0
410     Executive     US                   309366.0
441     Senior        US                   362837.0
445     Senior        US                   386708.0
454     Senior        US                   254368.0

Por que procurar discrepâncias?

Discrepâncias são valores extremos
- podem não representar com precisão nossos dados
Podem alterar a média e o desvio padrão
Testes estatísticos e modelos de aprendizado de máquina precisam de dados distribuídos normalmente

O que fazer com discrepâncias?

Perguntas a fazer:

Por que essas discrepâncias existem?
- Cargos mais altos / outros países pagam mais
- Considere deixá-las no conjunto de dados

Os dados estão corretos?
- Pode ter ocorrido algum erro na coleta de dados?
  - Se for o caso, remova-os

Excluir discrepâncias

no_outliers = salaries[(salaries["Salary_USD"] > lower) & (salaries["Salary_USD"] < upper)]

print(no_outliers["Salary_USD"].describe())

count       509.000000
mean     100674.567780
std       53643.050057
min        3819.000000
25%       60928.000000
50%       95483.000000
75%      134059.000000
max      248257.000000
Name: Salary_USD, dtype: float64

Distribuição de salários

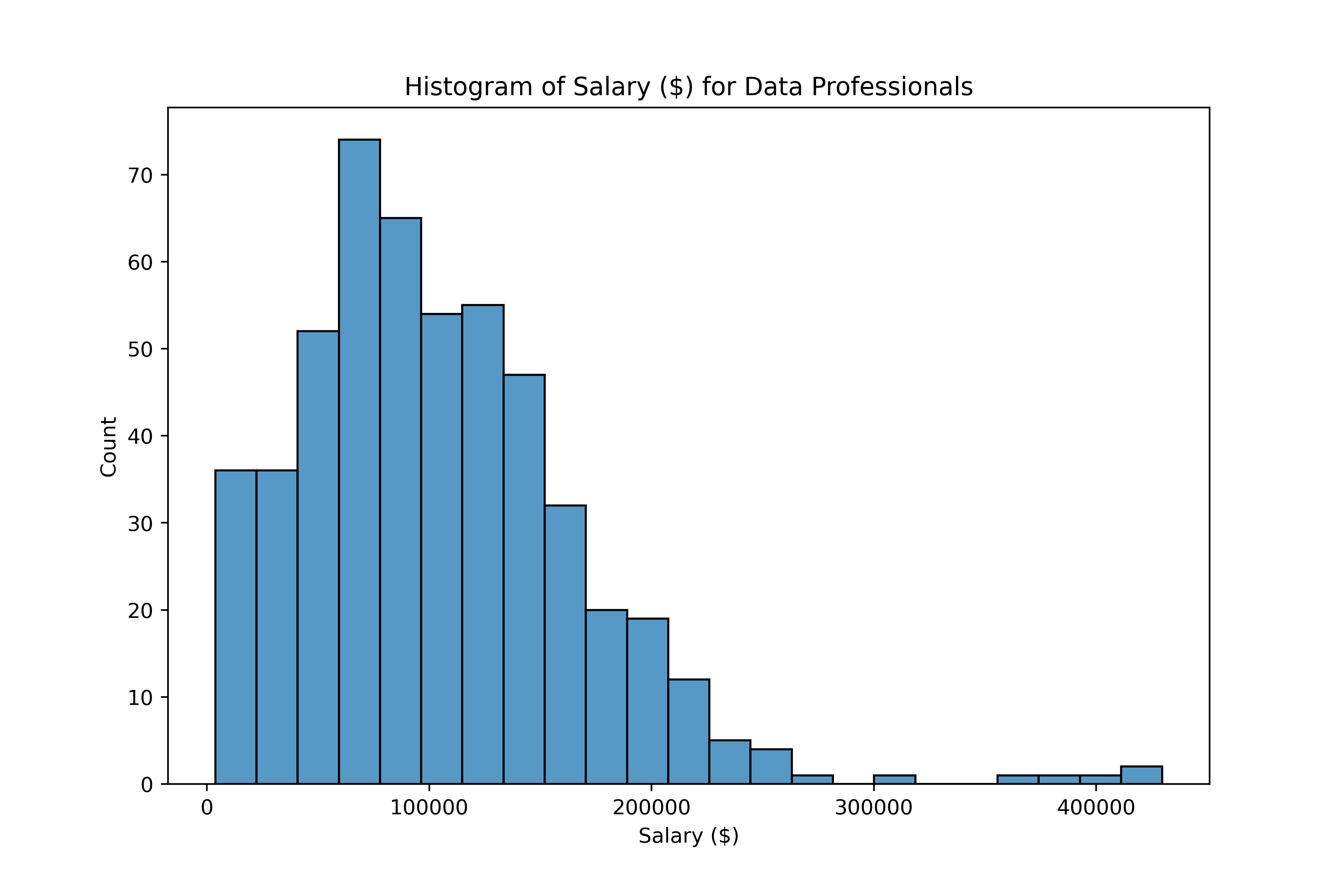
Histograma dos salários depois de substituir os valores atípicos pela mediana, com valores extremos entre cerca de 250.000 e 450.000 dólares.

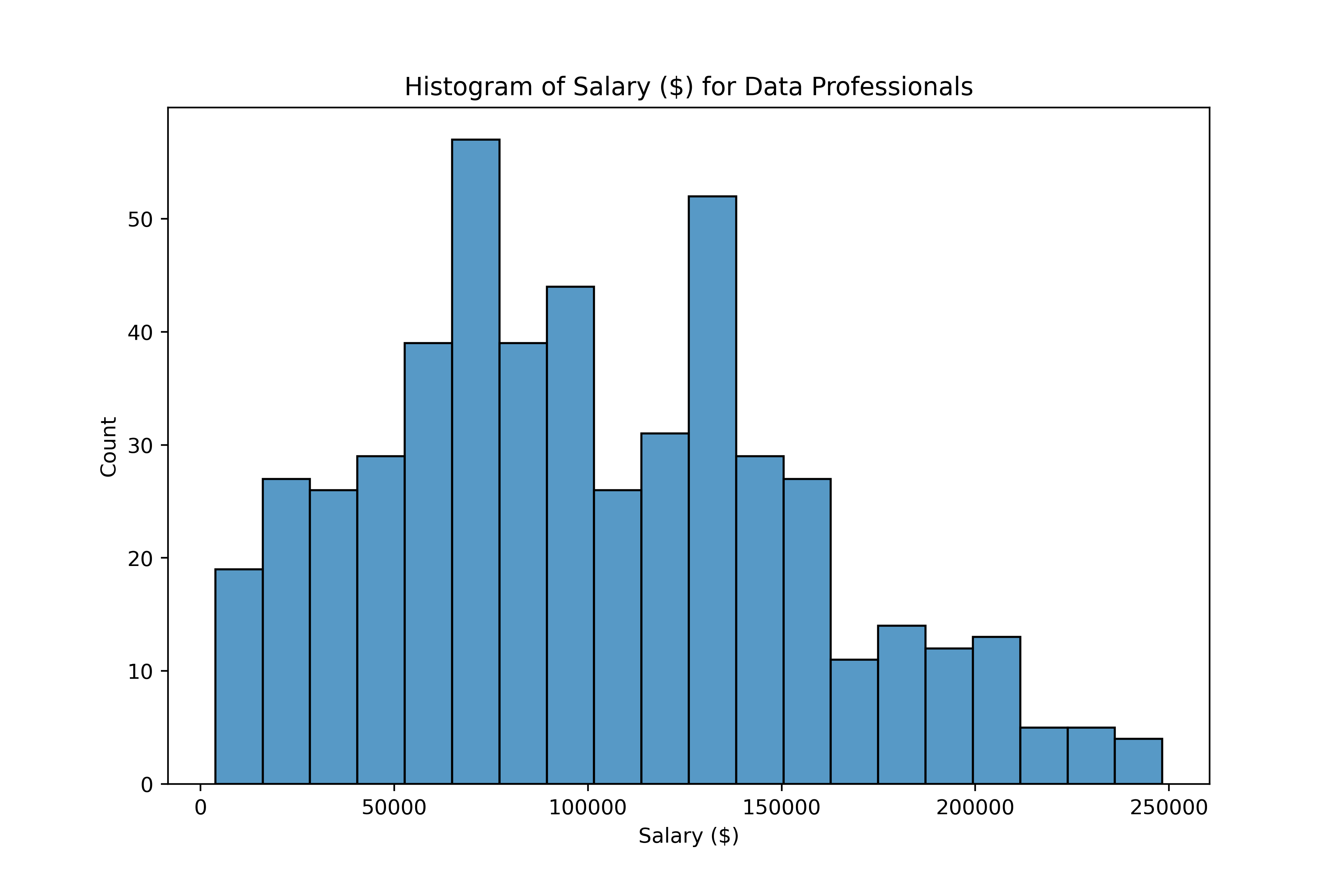
Histograma dos salários depois de substituir os valores atípicos pela mediana, que quase parece uma distribuição normal.

Vamos praticar!

Análise Exploratória de Dados em Python