Comparing sampling and bootstrap distributions

Sampling in Python

James Chapman

Curriculum Manager, DataCamp

Coffee focused subset

coffee_sample = coffee_ratings[["variety", "country_of_origin", "flavor"]]\
    .reset_index().sample(n=500)

     index         variety       country_of_origin  flavor
132    132           Other              Costa Rica    7.58
51      51            None  United States (Hawaii)    8.17
42      42  Yellow Bourbon                  Brazil    7.92
569    569         Bourbon               Guatemala    7.67
..     ...             ...                     ...     ...
643    643          Catuai              Costa Rica    7.42
356    356         Caturra                Colombia    7.58
494    494            None               Indonesia    7.58
169    169            None                  Brazil    7.81

[500 rows x 4 columns]

The bootstrap of mean coffee flavors

import numpy as np
mean_flavors_5000 = []
for i in range(5000):
    mean_flavors_5000.append(
        np.mean(coffee_sample.sample(frac=1, replace=True)['flavor'])
    )
bootstrap_distn = mean_flavors_5000

Mean flavor bootstrap distribution

import matplotlib.pyplot as plt
plt.hist(bootstrap_distn, bins=15)
plt.show()

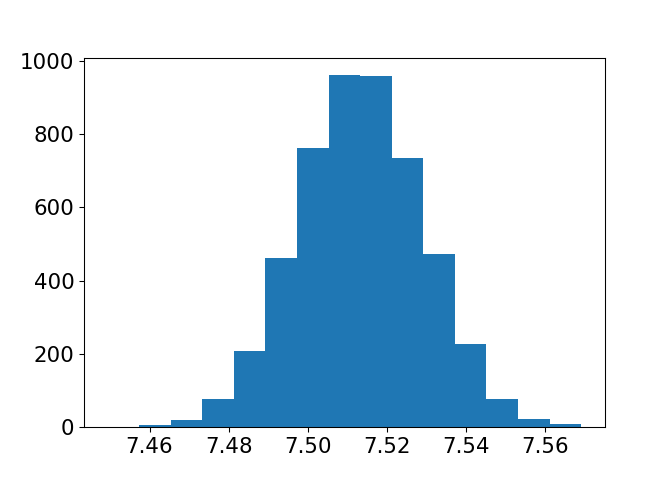
A histogram of the bootstrap distribution.

Sample, bootstrap distribution, population means

Sample mean:

coffee_sample['flavor'].mean()

7.5132200000000005

Estimated population mean:

np.mean(bootstrap_distn)

7.513357731999999

True population mean:

coffee_ratings['flavor'].mean()

7.526046337817639

Interpreting the means

Bootstrap distribution mean:

Usually close to the sample mean
May not be a good estimate of the population mean

Bootstrapping cannot correct biases from sampling

Sample sd vs. bootstrap distribution sd

Sample standard deviation:

coffee_sample['flavor'].std()

0.3540883911928703

Estimated population standard deviation?

np.std(bootstrap_distn, ddof=1)

0.015768474367958217

Sample, bootstrap dist'n, pop'n standard deviations

Sample standard deviation:

coffee_sample['flavor'].std()

0.3540883911928703

Estimated population standard deviation:

standard_error = np.std(bootstrap_distn, ddof=1)

Standard error is the standard deviation of the statistic of interest

True standard deviation:

coffee_ratings['flavor'].std(ddof=0)

0.34125481224622645

standard_error * np.sqrt(500)

0.3525938058821761

Standard error times square root of sample size estimates the population standard deviation

Interpreting the standard errors

Estimated standard error → standard deviation of the bootstrap distribution for a sample statistic
$\text{Population std. dev} \approx \text{Std. Error} \times \sqrt{\text{Sample size}}$

Let's practice!

Sampling in Python