Simpson's Paradox
Intermediate Regression in R

Richie Cotton
Data Evangelist at DataCamp
A most ingenious paradox!
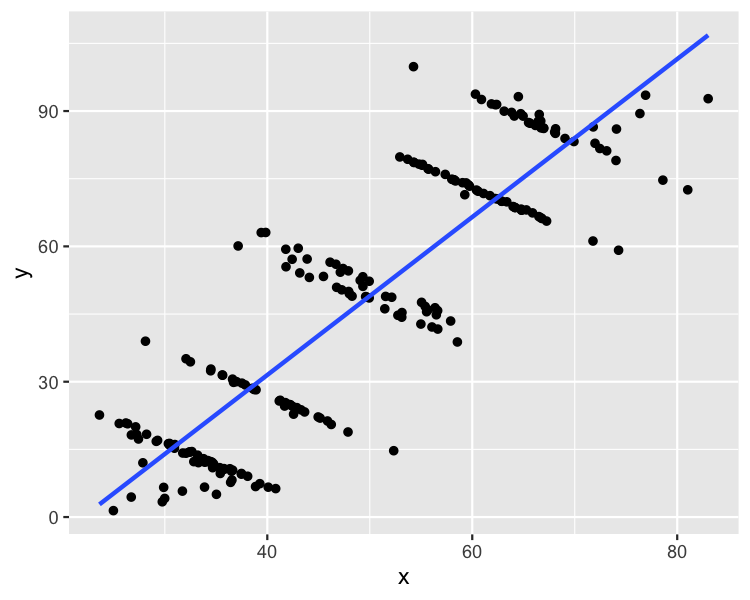
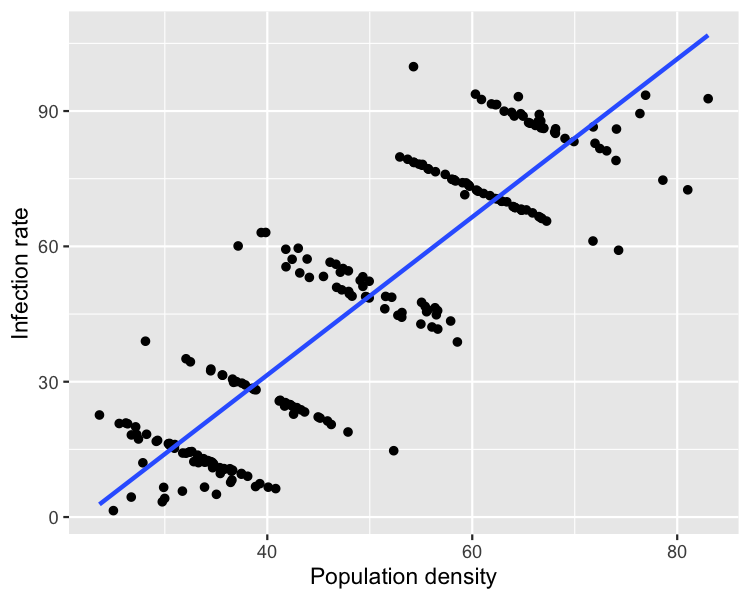
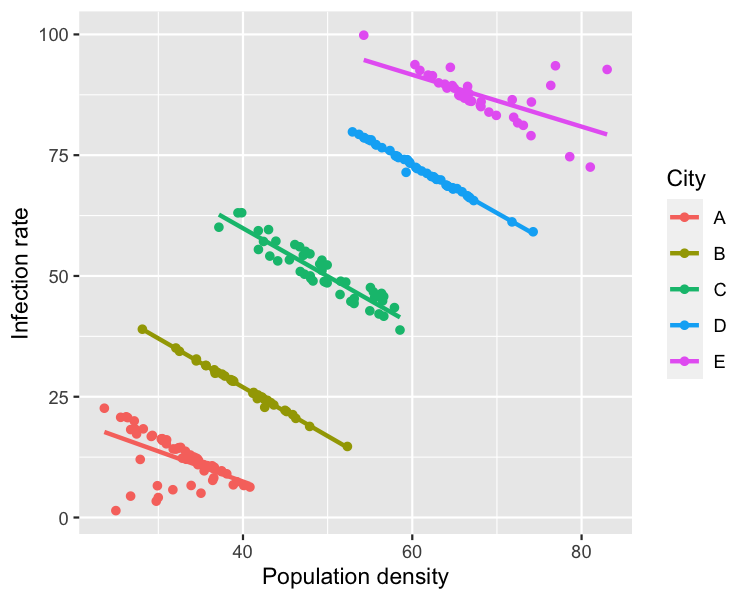
Simpson's Paradox occurs when the trend of a model on the whole dataset is very different from the trends shown by models on subsets of the dataset.
trend = slope coefficient
Synthetic Simpson data
| x | y | group |
|---|---|---|
| 62.24344 | 70.60840 | D |
| 52.33499 | 14.70577 | B |
| 56.36795 | 46.39554 | C |
| 66.80395 | 66.17487 | D |
| 66.53605 | 89.24658 | E |
| 62.38129 | 91.45260 | E |
- 5 groups of data, labeled "A" to "E"
1 https://www.rdocumentation.org/packages/datasauRus/topics/simpsons_paradox
Linear regressions
Whole dataset
mdl_whole <- lm(
y ~ x,
data = simpsons_paradox
)
coefficients(mdl_whole)
(Intercept) x
-38.554 1.751
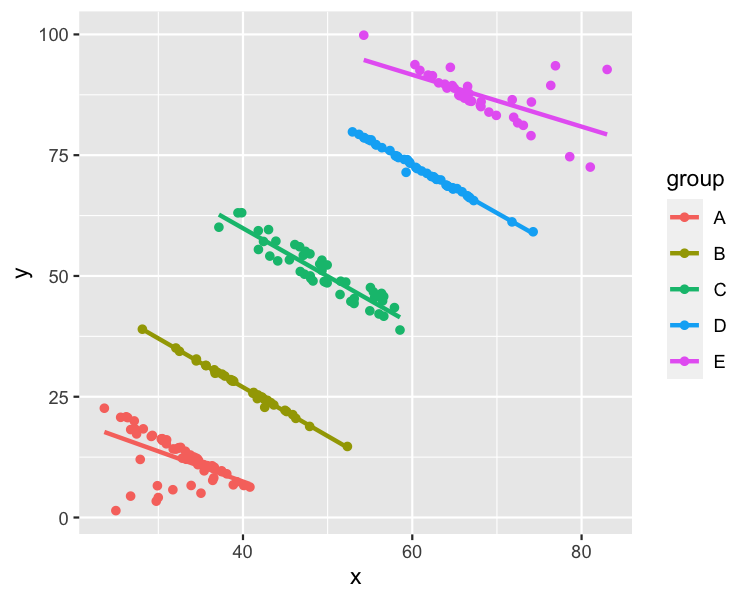
By group
mdl_by_group <- lm(
y ~ group + group:x + 0,
data = simpsons_paradox
)
coefficients(mdl_by_group)
groupA groupB groupC groupD groupE
32.5051 67.3886 99.6333 132.3932 123.8242
groupA:x groupB:x groupC:x groupD:x groupE:x
-0.6266 -1.0105 -0.9940 -0.9908 -0.5364
Plotting the whole dataset
ggplot(simpsons_paradox, aes(x, y)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE)
Plotting by group
ggplot(simpsons_paradox, aes(x, y, color = group)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE)
Reconciling the difference
Good advice
If possible, try to plot the dataset.
Common advice
You can't choose the best model in general—it depends on the dataset and the question you are trying to answer.
More good advice
Articulate a question before you start modeling.
Test score example
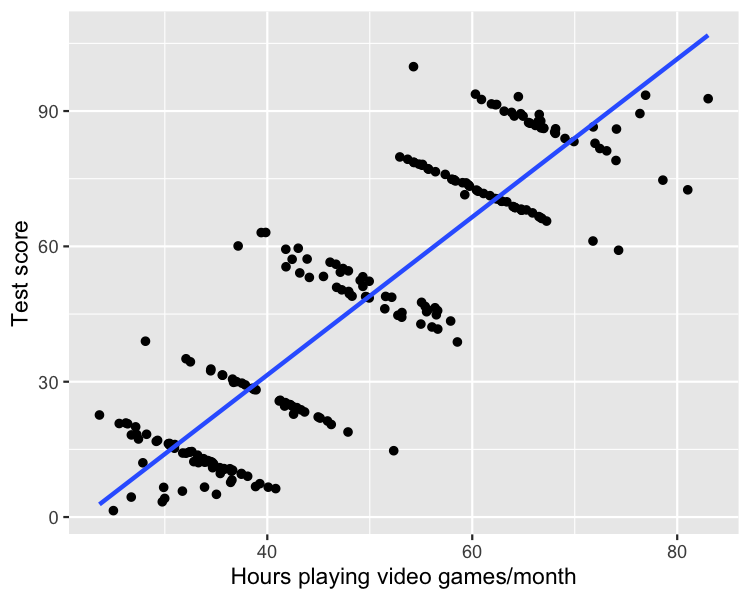
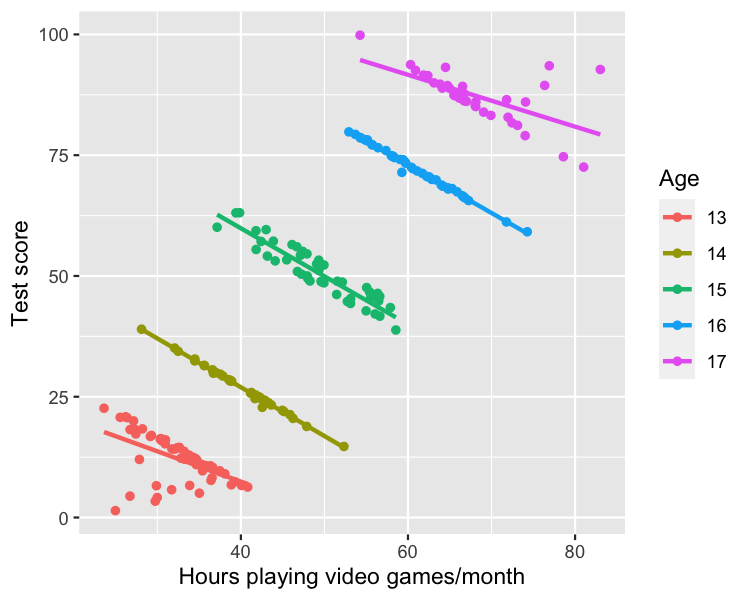
Infectious disease example
1 https://stats.stackexchange.com/questions/478463/examples-of-simpsons-paradox-being-resolved-by-choosing-the-aggregate-data
Reconciling the difference, again
- Usually (but not always) the grouped model contains more insight.
- Are you missing explanatory variables?
- Context is important.
Simpson's paradox in real datasets
- The paradox is usually less obvious.
- You may see a zero slope rather than a complete change in direction.
- It may not appear in every group.
Let's practice!
Intermediate Regression in R

