Descoberta de funções de ativação
Introdução ao Aprendizado Profundo com o PyTorch

Jasmin Ludolf
Senior Data Science Content Developer, DataCamp
Funções de ativação
$$
- As funções de ativação adicionam não linearidade à rede
- Sigmoide para classificação binária
- Softmax para classificação multiclasse
- Uma rede pode aprender relações mais complexas com não linearidade
- Saída de "pré-ativação" passada para a função de ativação

Conheça a função sigmoide
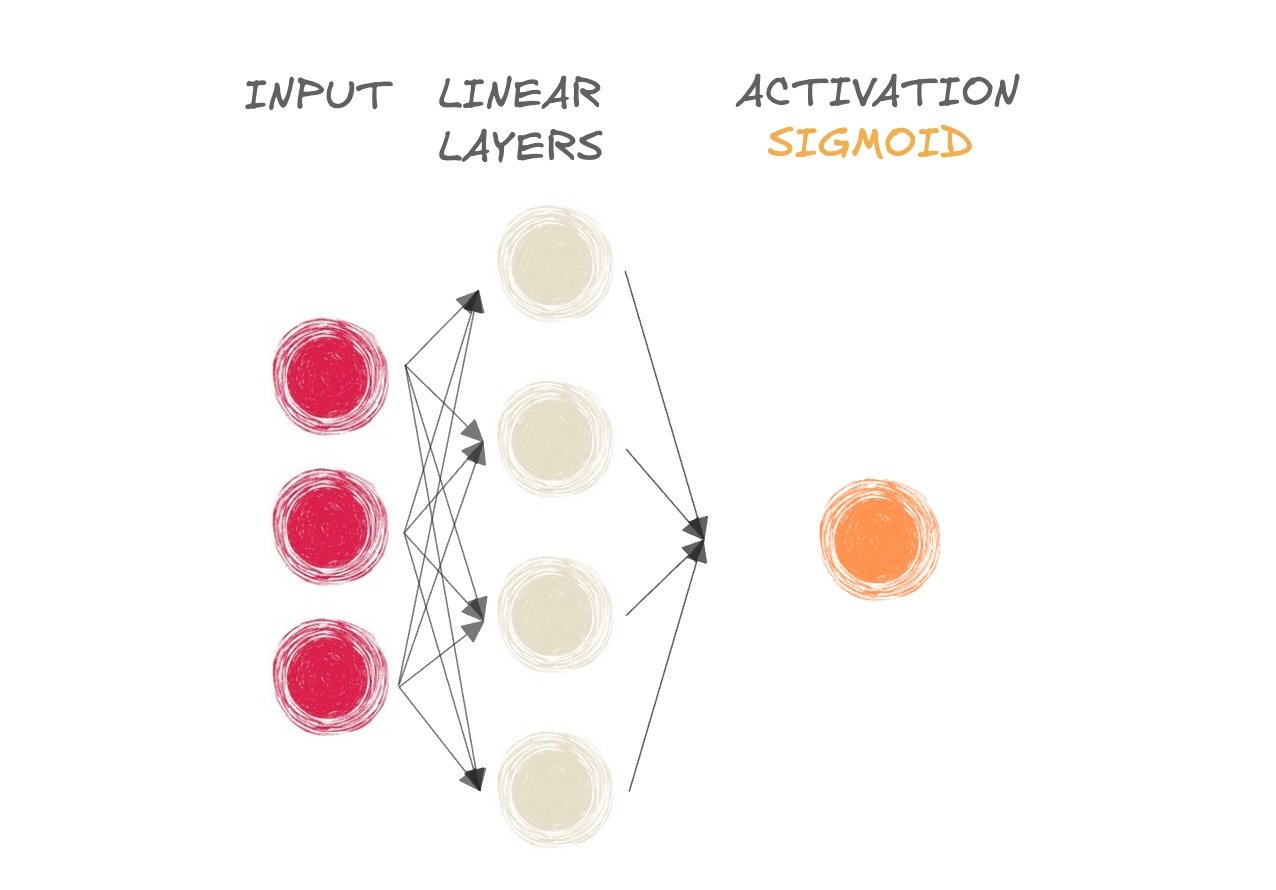
- Mamífero ou não?

Conheça a função sigmoide
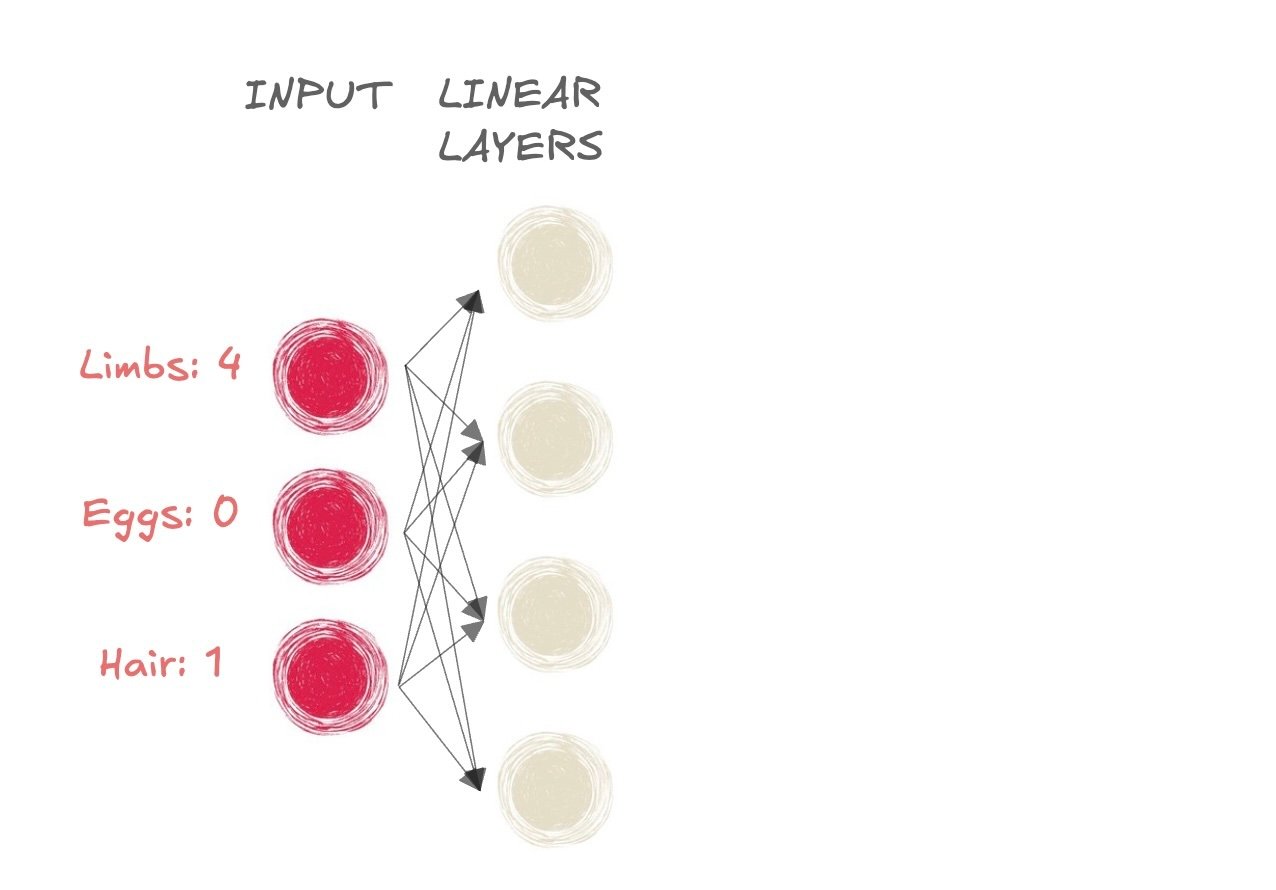
- Mamífero ou não?

- Entrada:
- Membros: 4
- Ovos: 0
- Pelo: 1
Conheça a função sigmoide
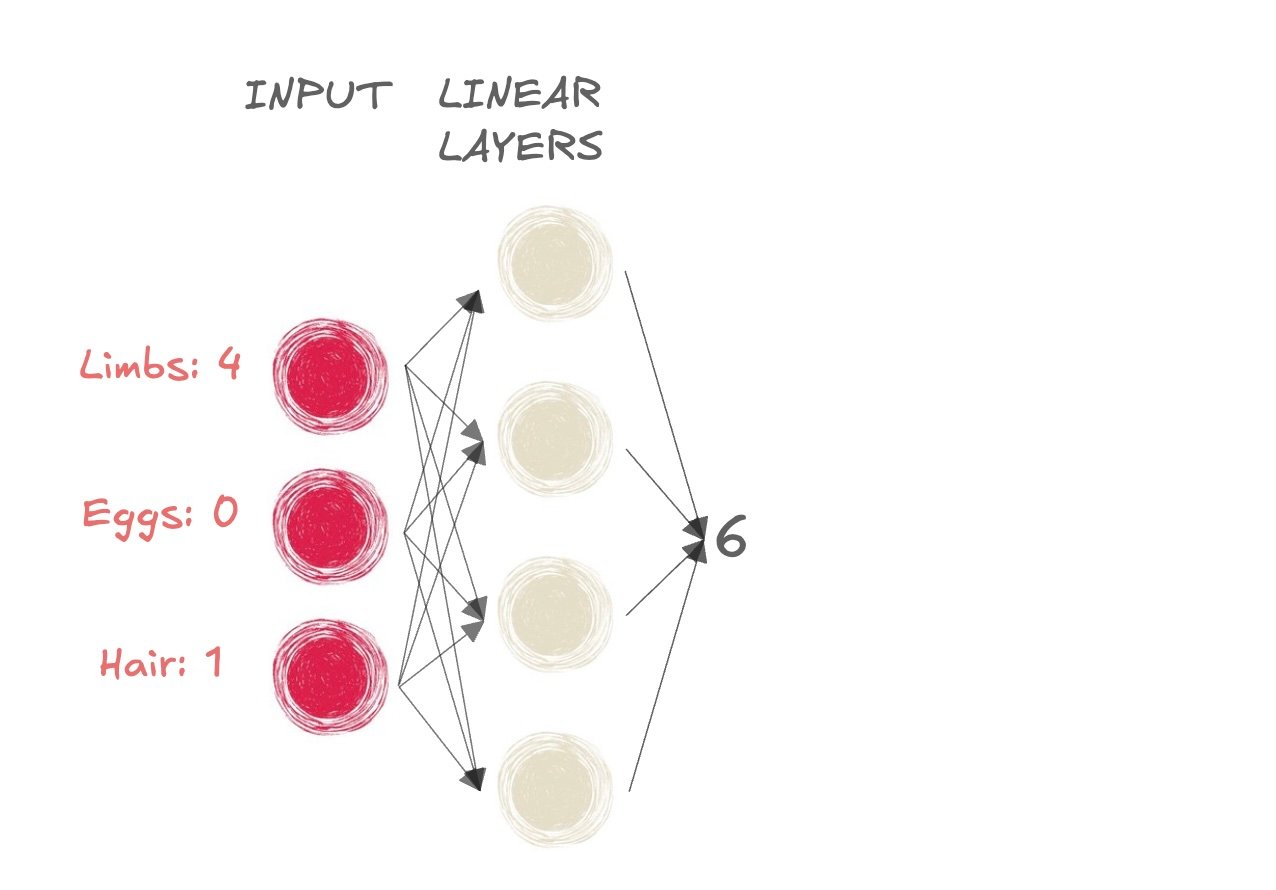
- Mamífero ou não?

- Saída para as camadas lineares é 6
Conheça a função sigmoide
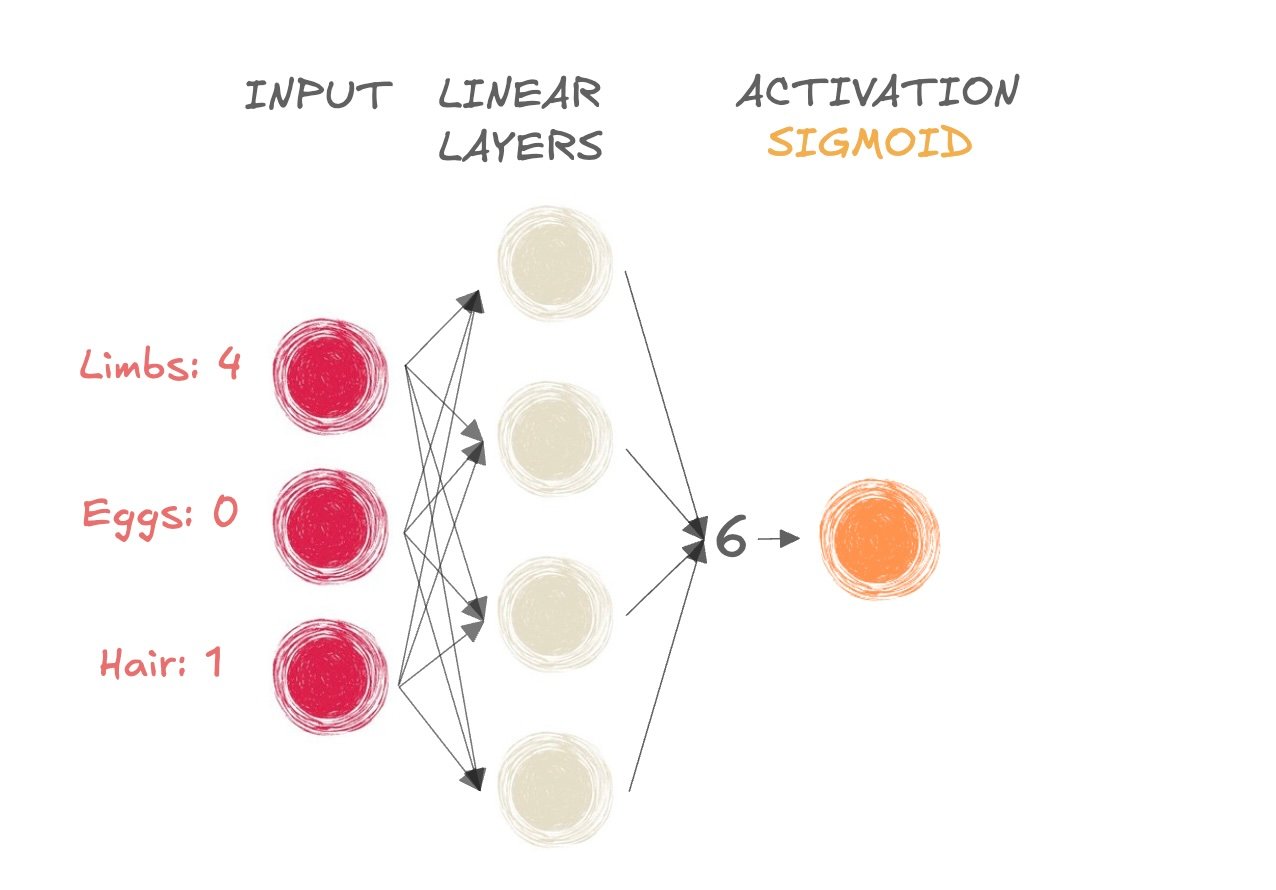
- Mamífero ou não?

- Pegamos o resultado da pré-ativação (6) e o passamos para a função sigmoide
Conheça a função sigmoide

- Mamífero ou não?

- Pegamos o resultado da pré-ativação (6) e o passamos para a função sigmoide
Obter um valor entre 0 e 1
Se resultado > 0.5, rótulo da classe = 1 (mamífero)
- Se resultado <= 0.5, rótulo da classe = 0 (não mamífero)
Conheça a função sigmoide
import torch import torch.nn as nn input_tensor = torch.tensor([[6]]) sigmoid = nn.Sigmoid()output = sigmoid(input_tensor) print(output)
tensor([[0.9975]])
Ativação como a última camada
model = nn.Sequential(
nn.Linear(6, 4), # First linear layer
nn.Linear(4, 1), # Second linear layer
nn.Sigmoid() # Sigmoid activation function
)
Sigmoide como última etapa na rede de camadas lineares é equivalente à regressão logística tradicional
Conhecendo a softmax
- Três classes:
Conhecendo a softmax
- Três classes:

Conhecendo a softmax
- Três classes:

Conhecendo a softmax
- Três classes:

Conhecendo a softmax

- Recebe três dimensões como entrada e produz a mesma forma
Conhecendo a softmax

- Recebe três dimensões como entrada e produz a mesma forma
- Gera uma distribuição de probabilidade:
- Cada elemento é uma probabilidade (limitada entre 0 e 1)
- A soma do vetor de saída é igual a 1
Conhecendo a softmax

- Recebe três dimensões como entrada e produz a mesma forma
- Gera uma distribuição de probabilidade:
- Cada elemento é uma probabilidade (limitada entre 0 e 1)
- A soma do vetor de saída é igual a 1
Conhecendo a softmax
import torch import torch.nn as nn # Create an input tensor input_tensor = torch.tensor( [[4.3, 6.1, 2.3]]) # Apply softmax along the last dimensionprobabilities = nn.Softmax(dim=-1) output_tensor = probabilities(input_tensor) print(output_tensor)
tensor([[0.1392, 0.8420, 0.0188]])
dim = -1indica que softmax é aplicada à última dimensão do tensor de entradann.Softmax()pode ser usado como última etapa emnn.Sequential()
Vamos praticar!
Introdução ao Aprendizado Profundo com o PyTorch

