Limitações da correlação

Introdução à estatística em Python

Maggie Matsui

Content Developer, DataCamp

Relações não lineares

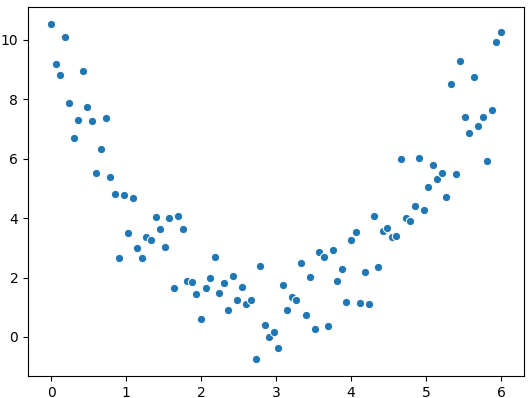
gráfico de dispersão de variáveis com uma relação quadrática

$$r = 0.18$$

Introdução à estatística em Python

Relações não lineares

O que vemos:

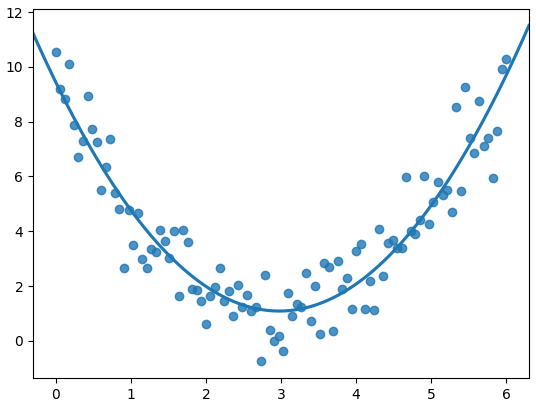
gráfico de dispersão de variáveis com uma relação quadrática com uma linha de tendência quadrática

O que o coeficiente de correlação vê:

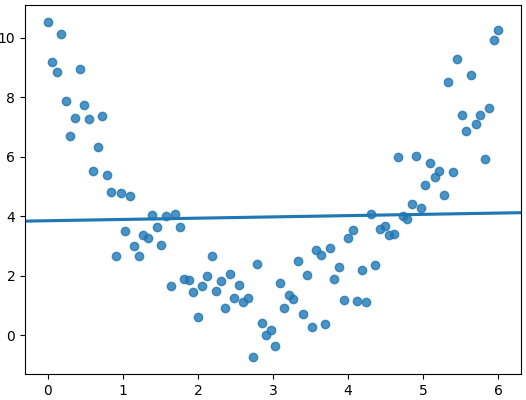
gráfico de dispersão de variáveis com uma relação quadrática com uma linha de tendência linear

Introdução à estatística em Python

A correlação só leva em conta as relações lineares

A correlação não deve ser usada às cegas

df['x'].corr(df['y'])

0.081094

Sempre visualize seus dados

gráfico de dispersão de variáveis com uma relação quadrática

Introdução à estatística em Python

Dados de sono de mamíferos

print(msleep)

                 name       genus   vore         order  ... sleep_cycle  awake  brainwt   bodywt
1             Cheetah    Acinonyx  carni     Carnivora  ...         NaN   11.9      NaN   50.000
2          Owl monkey       Aotus   omni      Primates  ...         NaN    7.0  0.01550    0.480
3     Mountain beaver  Aplodontia  herbi      Rodentia  ...         NaN    9.6      NaN    1.350
4 Greater short-ta...     Blarina   omni  Soricomorpha  ...    0.133333    9.1  0.00029    0.019
5                 Cow         Bos  herbi  Artiodactyla  ...    0.666667   20.0  0.42300  600.000
..                ...         ...    ...           ...  ...         ...    ...      ...      ...
79         Tree shrew      Tupaia   omni    Scandentia  ...    0.233333   15.1  0.00250    0.104
80 Bottle-nosed do...    Tursiops  carni       Cetacea  ...         NaN   18.8      NaN  173.330
81              Genet     Genetta  carni     Carnivora  ...         NaN   17.7  0.01750    2.000
82         Arctic fox      Vulpes  carni     Carnivora  ...         NaN   11.5  0.04450    3.380
83            Red fox      Vulpes  carni     Carnivora  ...    0.350000   14.2  0.05040    4.230
Introdução à estatística em Python

Peso corporal vs. tempo acordado

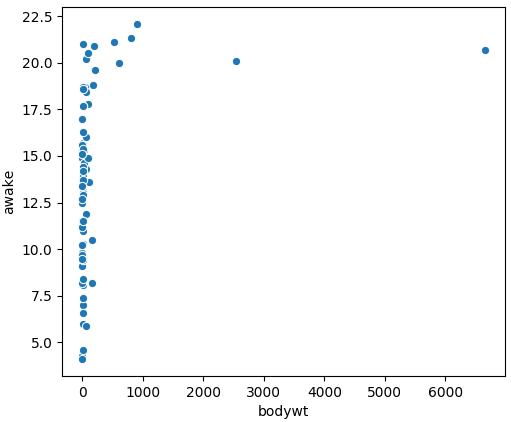
Gráfico de dispersão de peso corporal versus tempo acordado

msleep['bodywt'].corr(msleep['awake'])

0.3119801
Introdução à estatística em Python

Distribuição de peso corporal

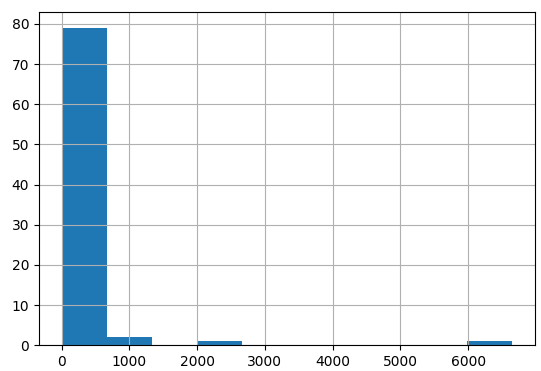
Histograma da variável bodywt

Introdução à estatística em Python

Transformação de log

msleep['log_bodywt'] = np.log(msleep['bodywt'])


sns.lmplot(x='log_bodywt',
           y='awake',
           data=msleep,
           ci=None)
plt.show()

msleep['log_bodywt'].corr(msleep['awake'])

0.5687943

![Gráfico de dispersão de log bodywt vs awake] (https://assets.datacamp.com/production/repositories/5786/datasets/233f47f84c9dabdff513e8e3871ab0f182fa0220/log_bodywt_vs_awake.png = 80)

Introdução à estatística em Python

Outras transformações

  • Transformação de log (log(x))
  • Transformação de raiz quadrada (sqrt(x))

  • Transformação recíproca (1 / x)

  • Combinações desses itens, como:

    • log(x) e log(y)
    • sqrt(x) e 1 / y
Introdução à estatística em Python

Por que usar uma transformação?

  • Certos métodos estatísticos dependem de variáveis que tenham uma relação linear
    • Coeficiente de correlação
    • Regressão linear

 

Introdução à modelagem linear em Python

Introdução à estatística em Python

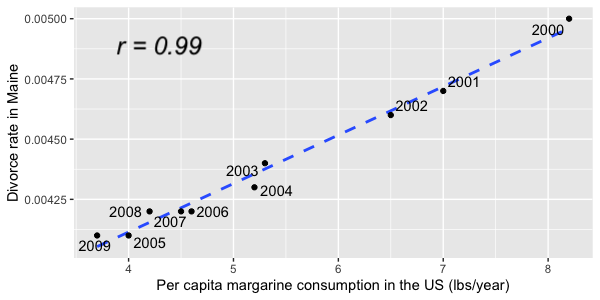
Correlação não implica causalidade

                x estar correlacionado com y não significa que x causa y

Gráfico de consumo de margarina per capita nos EUA em relação à taxa de divórcio no Maine. As variáveis estão altamente correlacionadas, com um coeficiente de correlação de 0,99

Introdução à estatística em Python

Fator de confusão

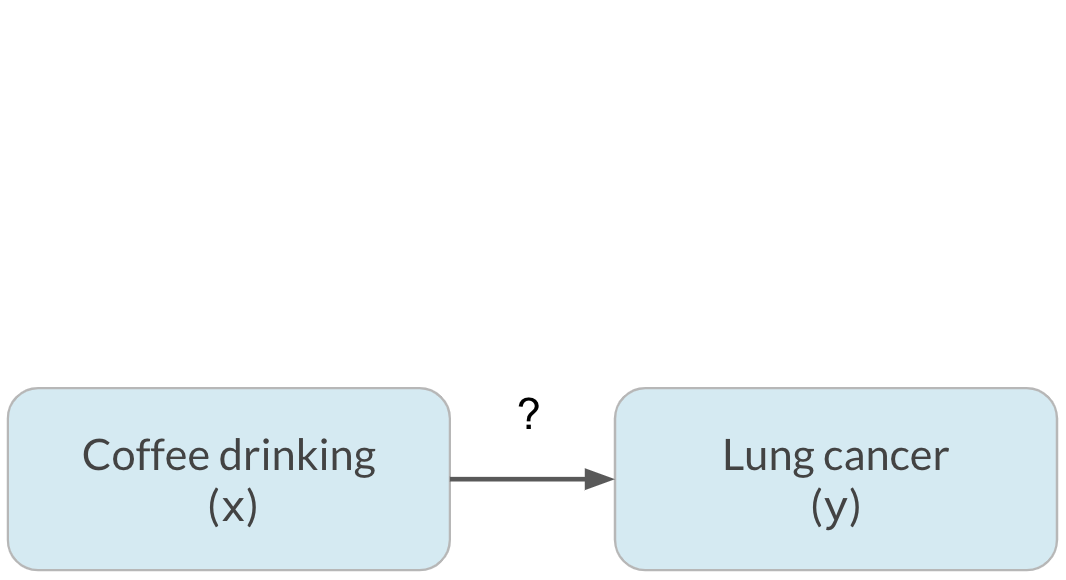
  O consumo de café (x) aponta para o câncer de pulmão (y)

Introdução à estatística em Python

Fator de confusão

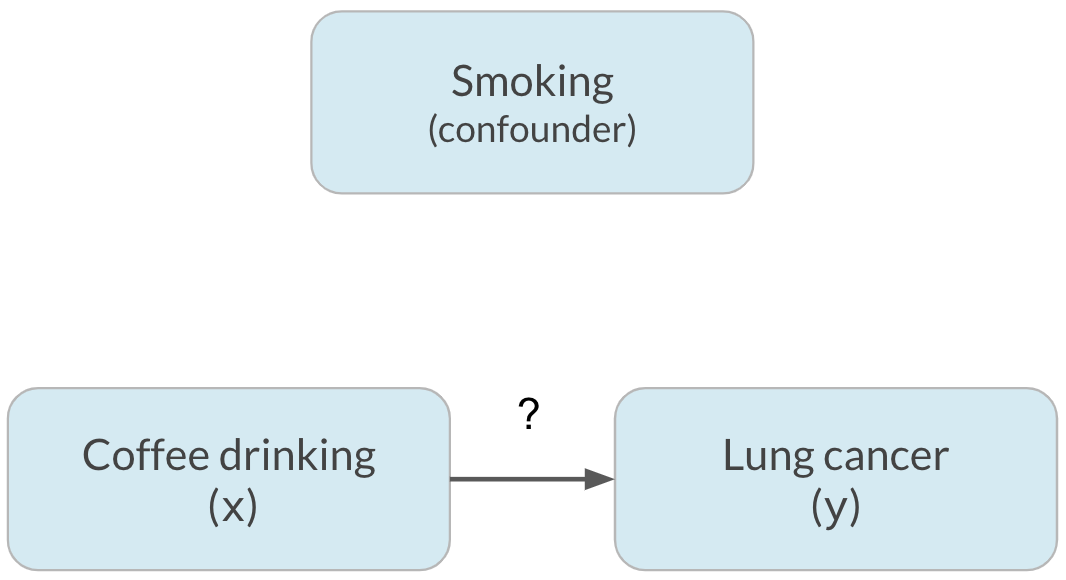
  O consumo de café (x) aponta para câncer de pulmão (y) com tabagismo (fator de confusão) acima

Introdução à estatística em Python

Fator de confusão

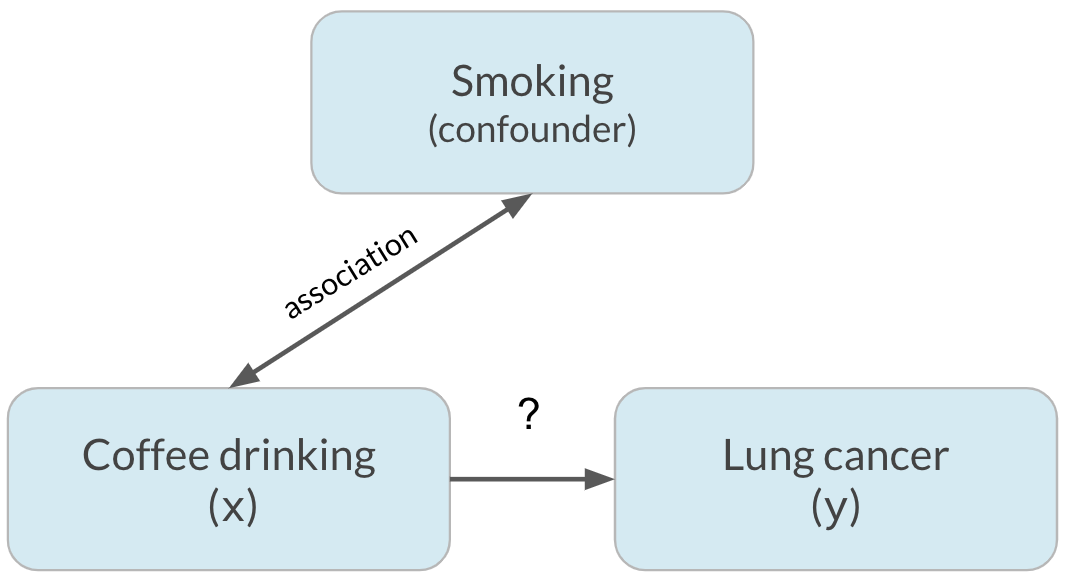
  O consumo de café (x) aponta para câncer de pulmão (y) com tabagismo (fator de confusão). Seta dupla entre tabagismo e consumo de café, rotulada como "associação".

Introdução à estatística em Python

Fator de confusão

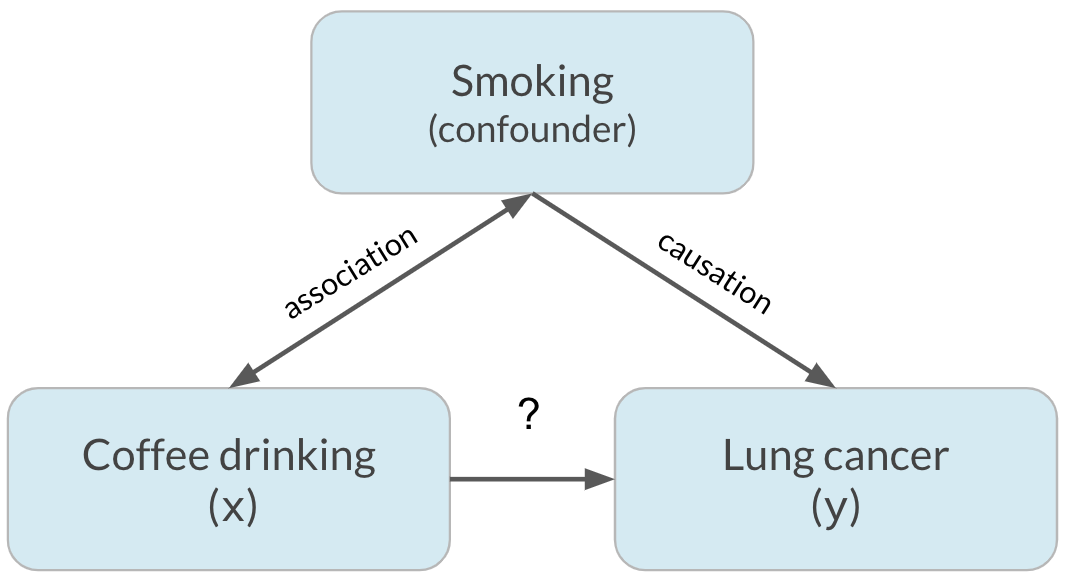
  O consumo de café (x) aponta para câncer de pulmão (y) com tabagismo (fator de confusão). Seta dupla entre tabagismo e consumo de café, rotulada como "associação". Seta do tabagismo para o câncer de pulmão rotulada como "causalidade"

Introdução à estatística em Python

Fator de confusão

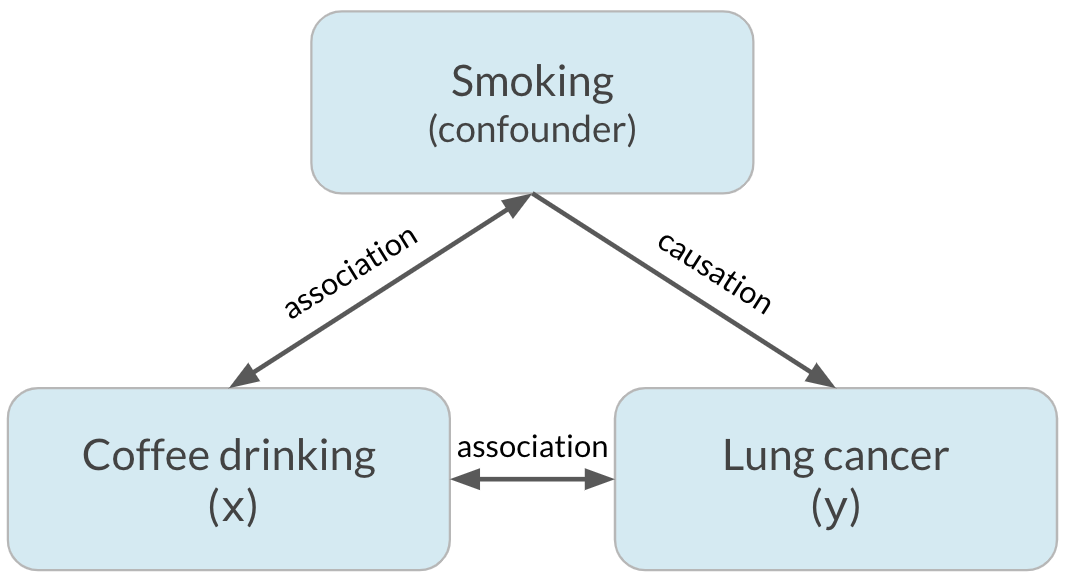
  Consumo de café (x) com seta dupla para o câncer de pulmão (y) rotulado como "associação". Seta dupla entre tabagismo e consumo de café, rotulada como "associação". Seta do tabagismo para o câncer de pulmão rotulada como "causalidade".

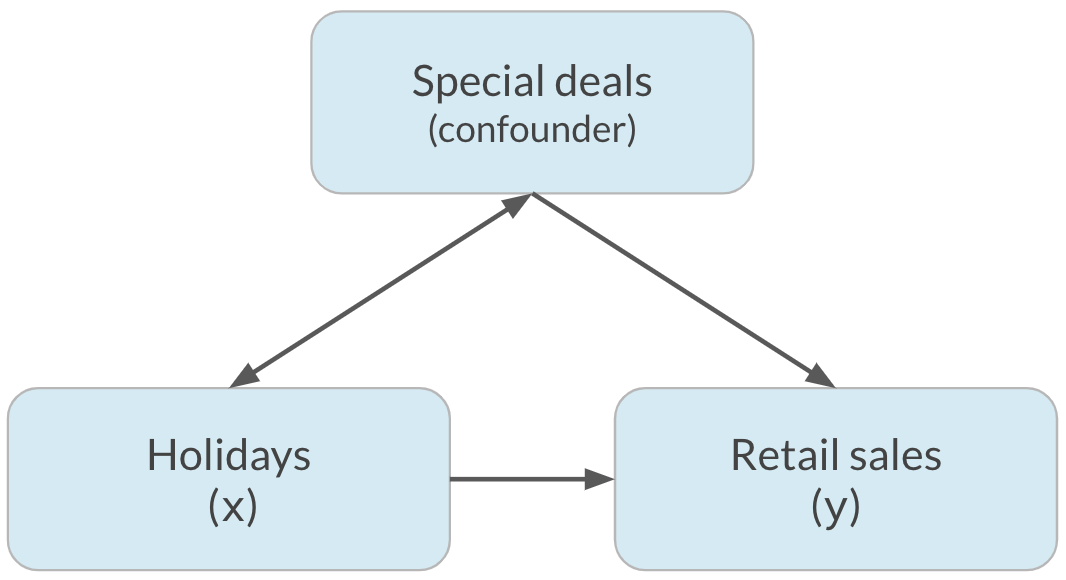
  Feriados (x) apontam para vendas no varejo (y). Ofertas especiais (fator de confusão) têm uma seta dupla para feriados e uma seta simples para vendas no varejo.

Introdução à estatística em Python

Vamos praticar!

Introdução à estatística em Python

Preparing Video For Download...