Quais são as chances?
Introdução à estatística em Python

Maggie Matsui
Content Developer, DataCamp
Medindo a chance
Qual é a probabilidade de um evento?
$$ P(\text{event}) = \frac{\text{\# ways event can happen}}{\text{total \# of possible outcomes}} $$
Exemplo: cara ou coroa
$$ P(\text{heads}) = \frac{\text{1 way to get heads}}{\text{2 possible outcomes}} = \frac{1}{2} = 50\%$$

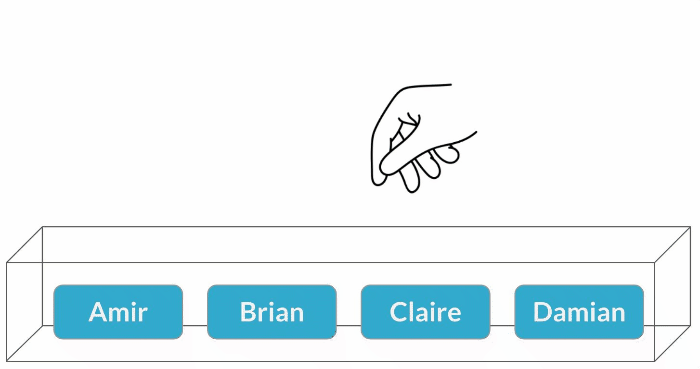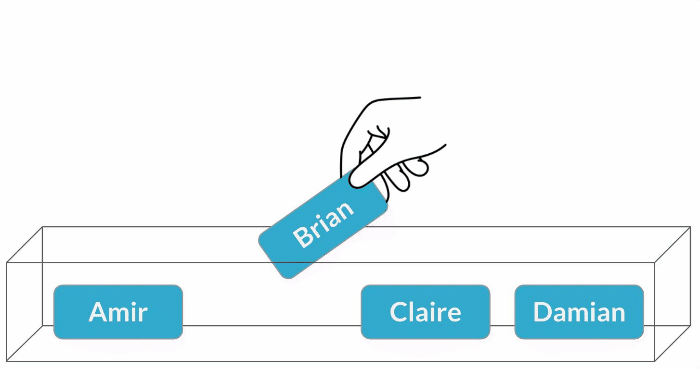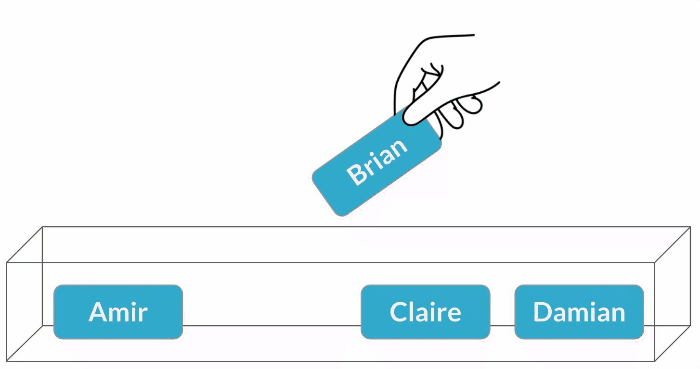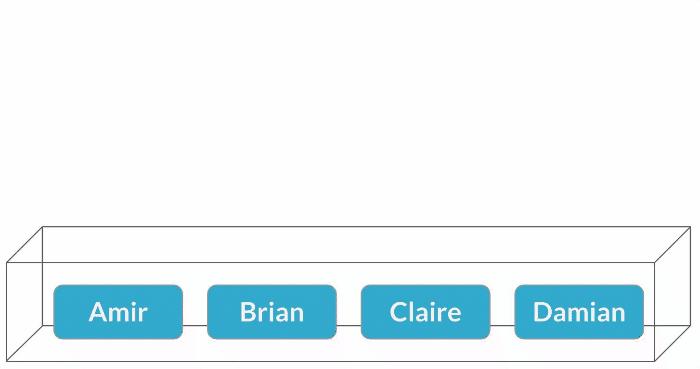
Atribuição de vendedores
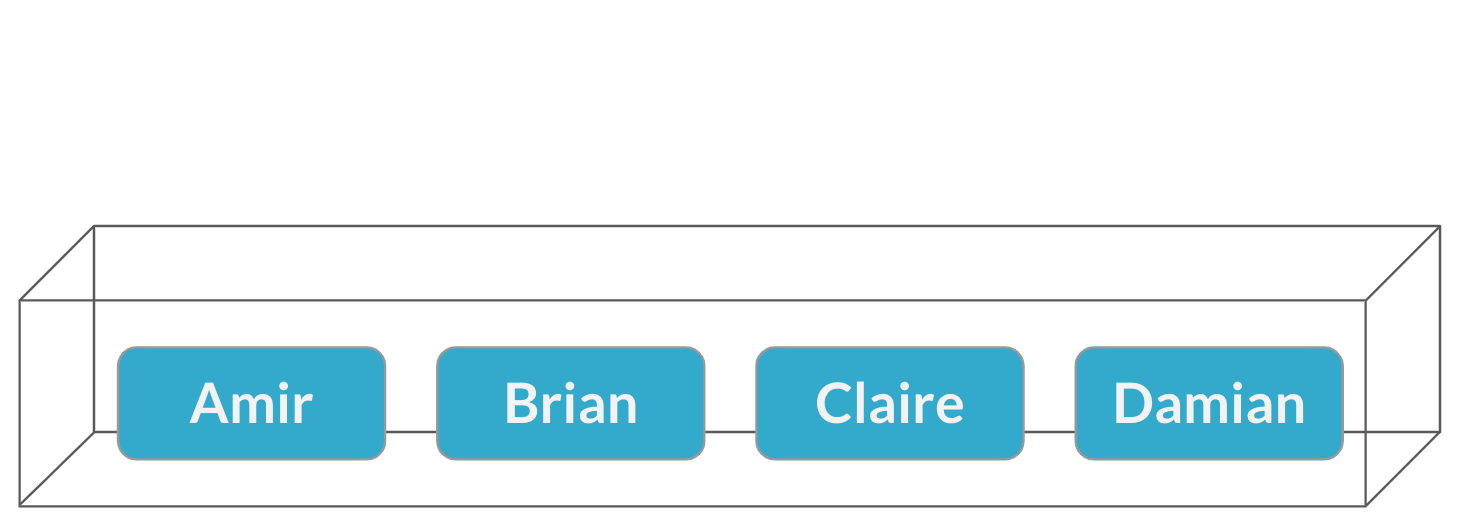
Atribuição de vendedores
$$P(\text{Brian}) = \frac{1}{4} = 25\%$$
Amostragem de um DataFrame
print(sales_counts)
name n_sales
0 Amir 178
1 Brian 128
2 Claire 75
3 Damian 69
sales_counts.sample()
name n_sales
1 Brian 128
sales_counts.sample()
name n_sales
2 Claire 75
Definir uma semente aleatória
np.random.seed(10)sales_counts.sample()
name n_sales
1 Brian 128
np.random.seed(10)
sales_counts.sample()
name n_sales
1 Brian 128
np.random.seed(10)
sales_counts.sample()
name n_sales
1 Brian 128
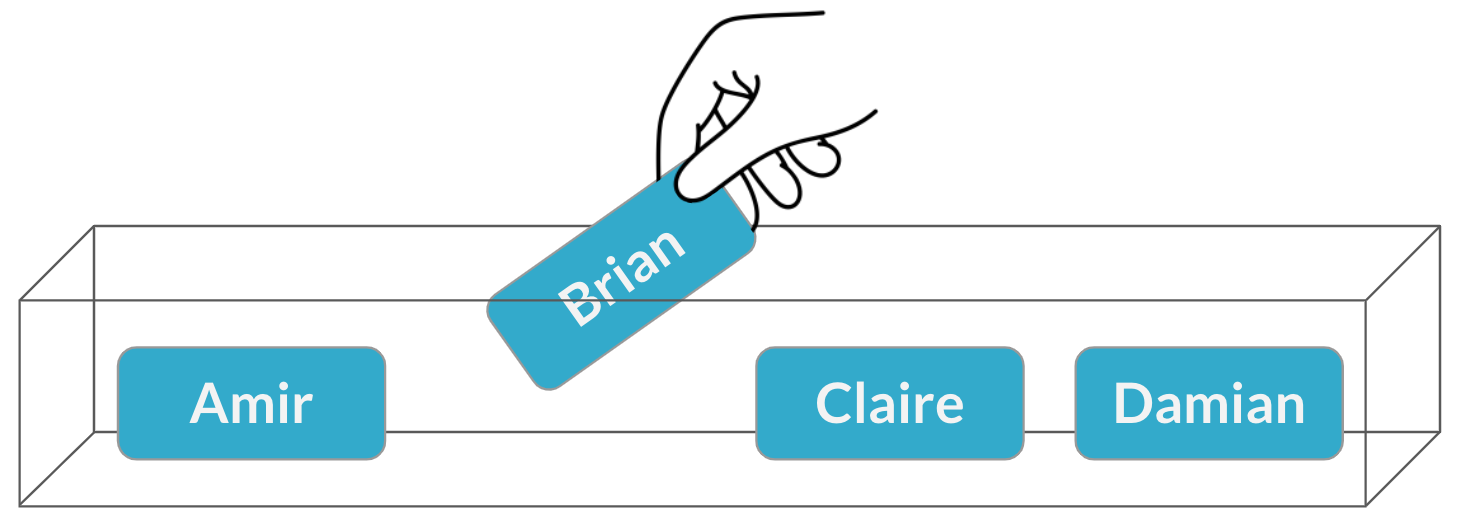
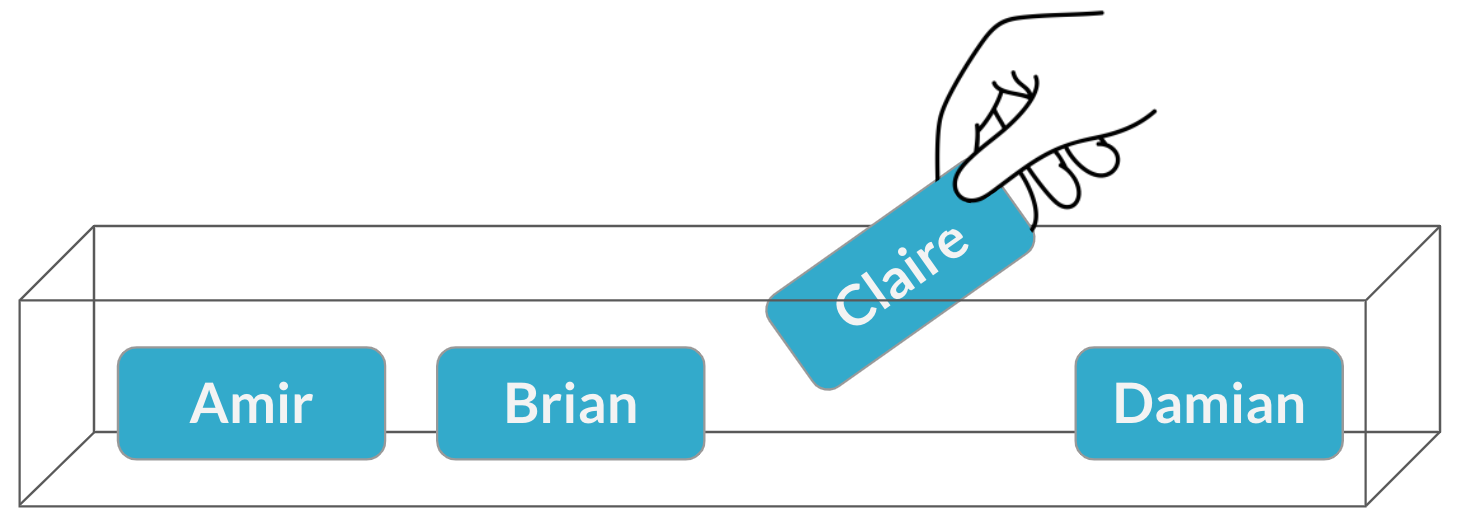
Uma segunda reunião
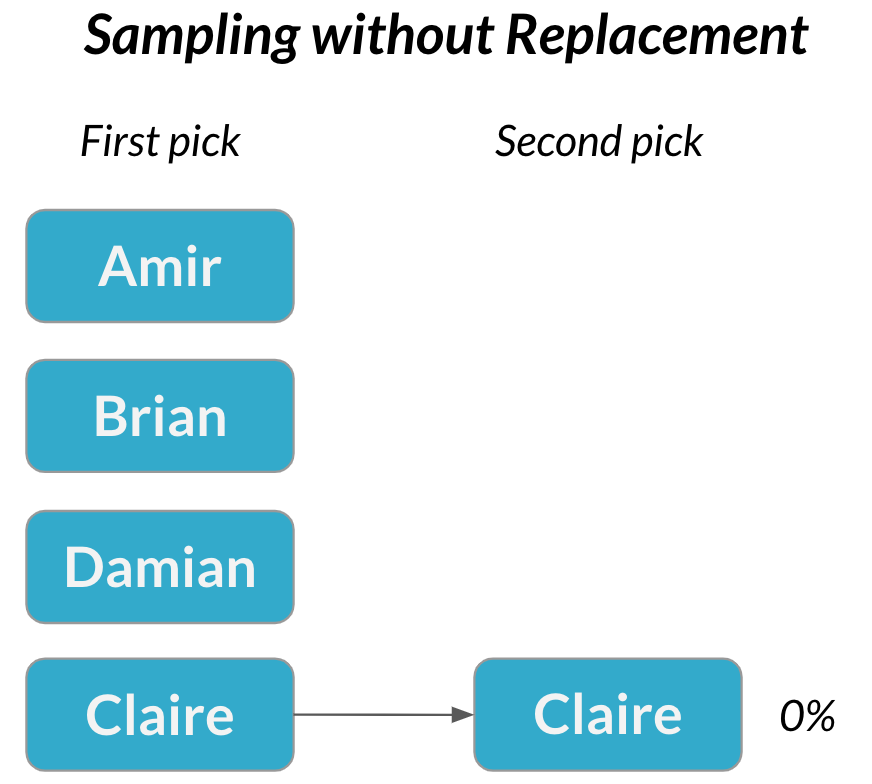
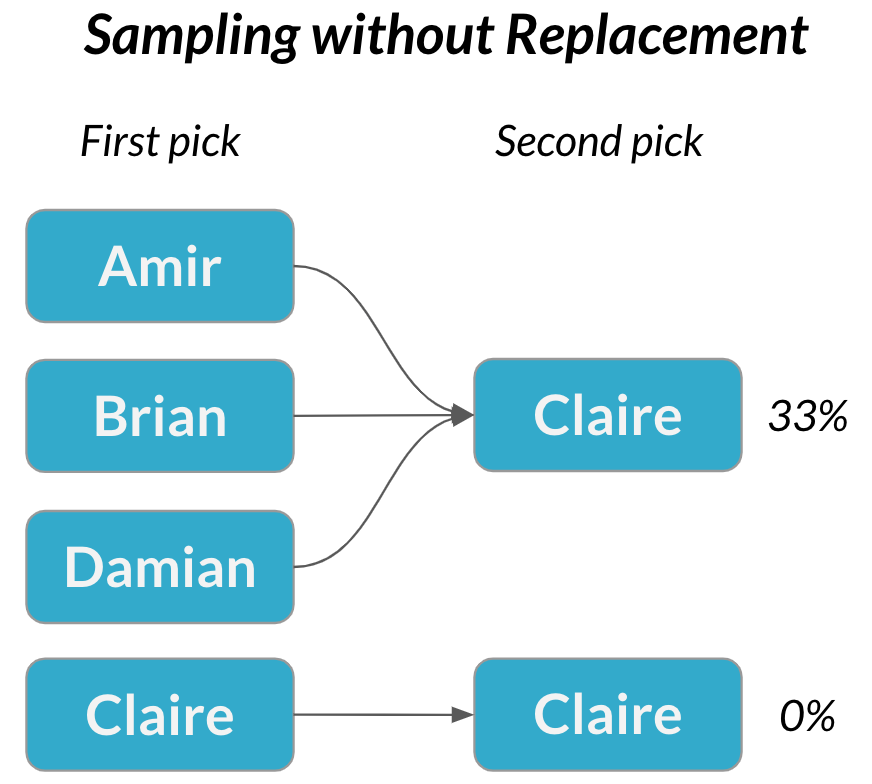
Amostragem sem substituição

Uma segunda reunião
$$P(\text{Claire}) = \frac{1}{3} = 33\%$$
Amostragem dupla em Python
sales_counts.sample(2)
name n_sales
1 Brian 128
2 Claire 75
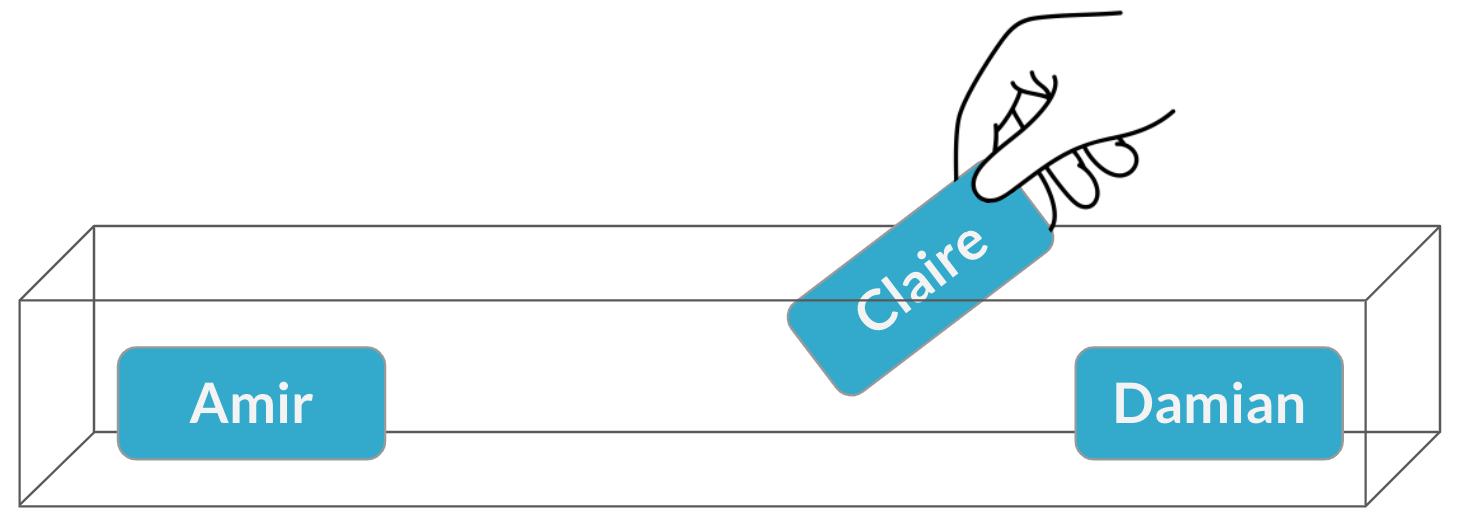
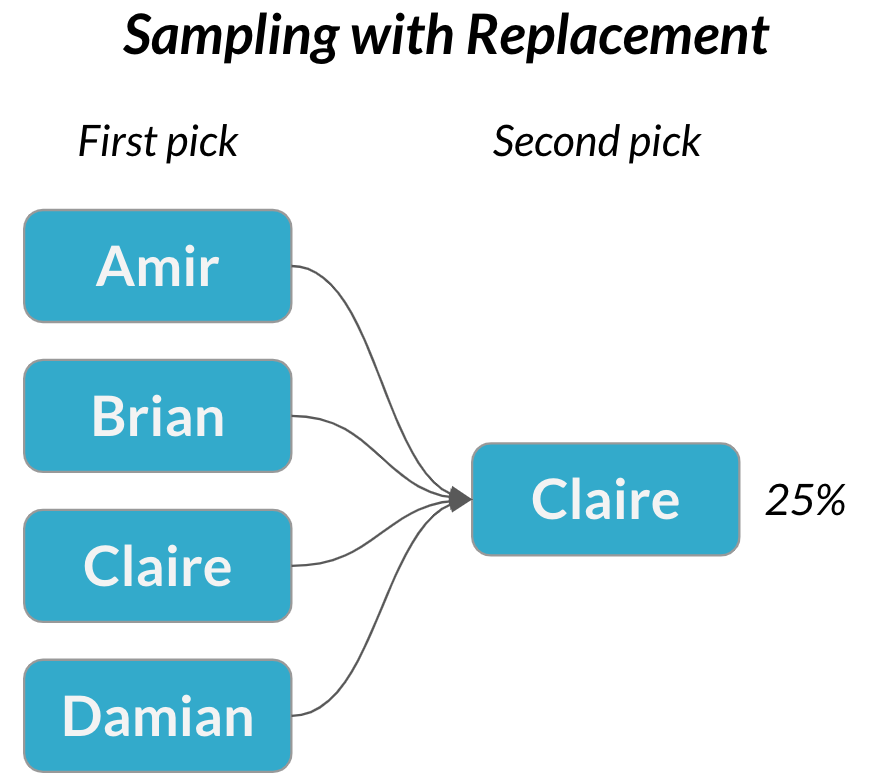
Amostragem com substituição
Amostragem com substituição
$$P(\text{Claire}) = \frac{1}{4} = 25\%$$
Amostragem com/sem substituição em Python
sales_counts.sample(5, replace = True)
name n_sales
1 Brian 128
2 Claire 75
1 Brian 128
3 Damian 69
0 Amir 178
Eventos independentes
Dois eventos são independentes se a probabilidade do segundo evento não for afetada pelo resultado do primeiro evento.

Eventos independentes
Dois eventos são independentes se a probabilidade do segundo evento não for afetada pelo resultado do primeiro evento.
Amostragem com reposição = cada seleção é independente
Eventos dependentes
Dois eventos são dependentes se a probabilidade do segundo evento for afetada pelo resultado do primeiro evento.

Eventos dependentes
Dois eventos são dependentes se a probabilidade do segundo evento for afetada pelo resultado do primeiro evento.
Eventos dependentes
Dois eventos são dependentes se a probabilidade do segundo evento for afetada pelo resultado do primeiro evento.
Amostragem sem reposição → escolhas se tornam dependentes
Vamos praticar!
Introdução à estatística em Python

