A distribuição binomial

Introdução à estatística em Python

Maggie Matsui

Content Developer, DataCamp

Lançar moeda

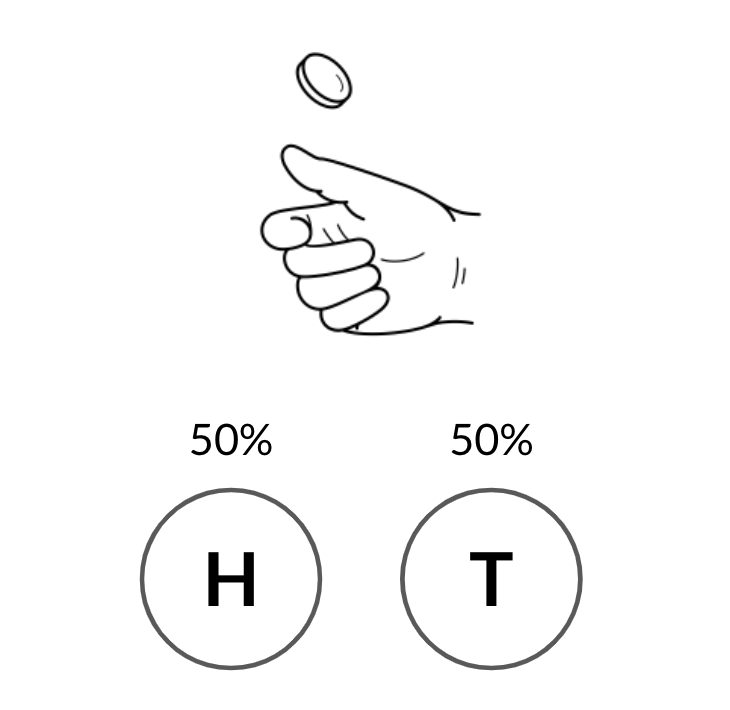
Mão lançando moeda com um lado com 50% de chance e o outro lado com 50% de chance

Introdução à estatística em Python

Resultados binários

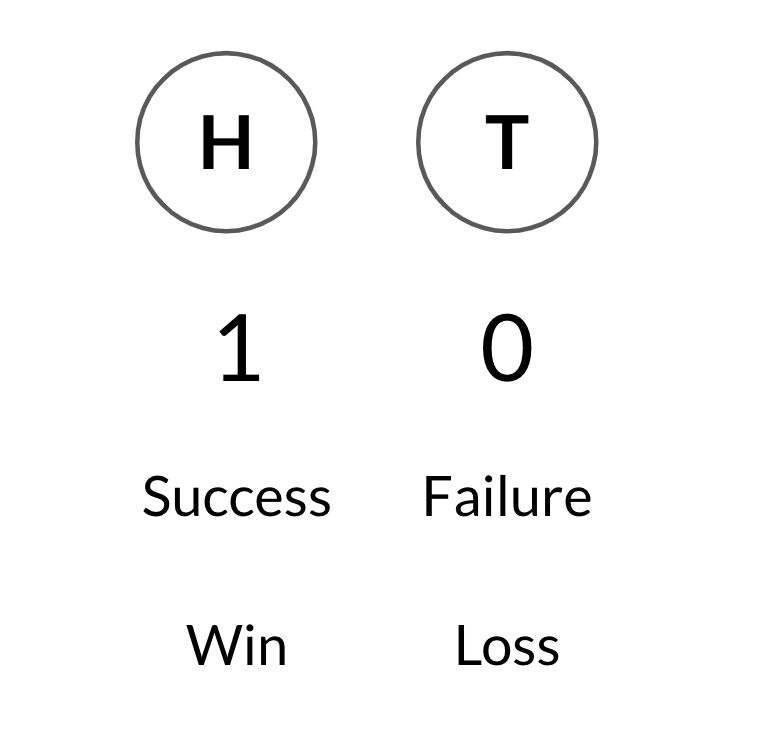
H e T, 1 e 0, sucesso e fracasso, vitória e derrota

Introdução à estatística em Python

Um único lance

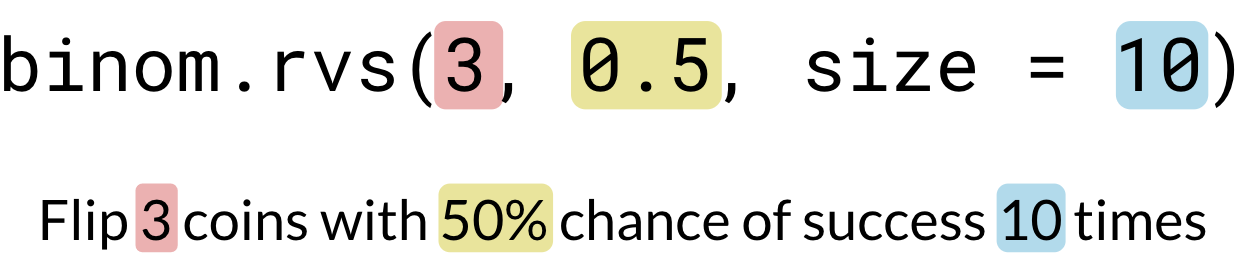
binom.rvs(# of coins, probability of heads/success, size=# of trials)

1 = cara, 0 = coroa

from scipy.stats import binom

binom.rvs(1, 0.5, size=1)

array([1])
Introdução à estatística em Python

Um lance muitas vezes

binom.rvs(1, 0.5, size=8)

array([0, 1, 1, 0, 1, 0, 1, 1])

 

binom.rvs(1, 0.5, 8) com 1 em vermelho, 0.5 em amarelo e 8 em azul. Texto: Lance 1 (em vermelho) moeda com 50% (em amarelo) de chance de sucesso 8 (em azul) vezes

Introdução à estatística em Python

Muitos lances uma vez

binom.rvs(8, 0.5, size=1)

array([5])

 

binom.rvs(8, 0.5, size=1) com 8 em vermelho, 0.5 em amarelo e 1 em azul. Texto: Lance 8 (em vermelho) moedas com 50% (em amarelo) de chance de sucesso 1 (em azul) vez

Introdução à estatística em Python

Muitos lances muitas vezes

binom.rvs(3, 0.5, size=10)

array([0, 3, 2, 1, 3, 0, 2, 2, 0, 0])

 

binom.rvs(3, 0.5, size=10) com 3 em vermelho, 0.5 em amarelo e 10 em azul. Texto: Lance 3 (em vermelho) moedas com 50% (em amarelo) de chance de sucesso 10 (em azul) vezes

Introdução à estatística em Python

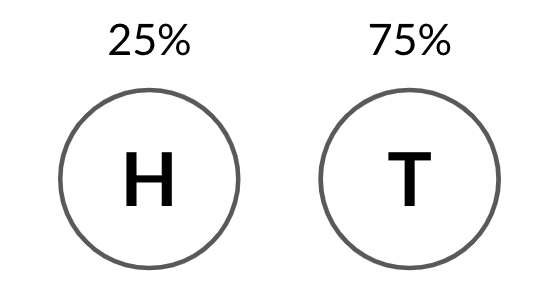
Outras probabilidades

binom.rvs(3, 0.25, size=10)

array([1, 1, 1, 1, 0, 0, 2, 0, 1, 0])

 

Imagem de cara com 25% de probabilidade e coroa com 75% de probabilidade

Introdução à estatística em Python

Distribuição binomial

Distribuição de probabilidade de sucessos em uma sequência de tentativas independentes

Ex.: número de caras em uma sequência de lançamentos de moedas

Descrito por $n$ e $p$

  • $n$: número total de tentativas
  • $p$: probabilidade de sucesso
binom.rvs(n=10, p=0.5, size=20)

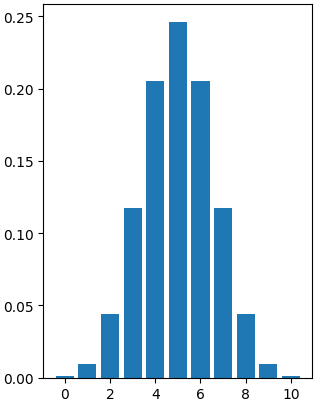
Gráfico da distribuição binomial com n=10, p = 0,5

Introdução à estatística em Python

Qual é a probabilidade de 7 caras?

$P(\text{heads} = 7)$

# binom.pmf(num heads, num trials, prob of heads)
binom.pmf(7, 10, 0.5)

0.1171875
Introdução à estatística em Python

Qual é a probabilidade de 7 ou menos caras?

$P(\text{heads} \le 7)$

binom.cdf(7, 10, 0.5)

0.9453125
Introdução à estatística em Python

Qual é a probabilidade de mais de 7 caras?

$P(\text{heads} > 7)$

1 - binom.cdf(7, 10, 0.5)

0.0546875
Introdução à estatística em Python

Valor esperado

$\text{Expected value} = n \times p$

_Número esperado de caras em 10 lances _ $= 10 \times 0,5 = 5$

Introdução à estatística em Python

Independência

_Distribuição binomial é uma distribuição de probabilidade de sucessos em uma sequência de tentativas independentes _

Caixa de bilhetes com 3 zeros e 3 uns. 50% de chance de 0, 50% de chance de 1

Introdução à estatística em Python

Independência

_Distribuição binomial é uma distribuição de probabilidade de sucessos em uma sequência de tentativas independentes _

 

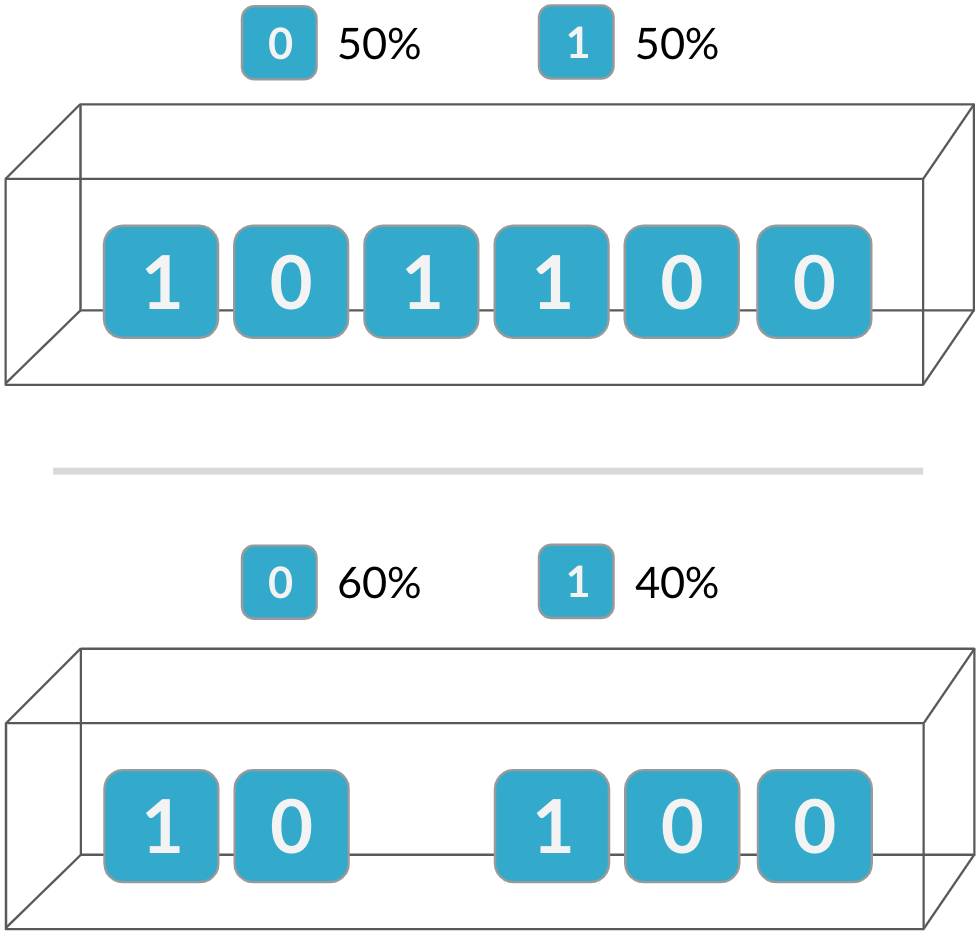
As probabilidades da segunda tentativa mudam devido ao resultado da primeira

 

Se as tentativas não forem independentes, a distribuição binomial não se aplica!

Caixa de bilhetes com 3 zeros e 2 uns. 60% de chance de 0, 40% de chance de 1

Introdução à estatística em Python

Vamos praticar!

Introdução à estatística em Python

Preparing Video For Download...