Distribuições discretas
Introdução à estatística em Python

Maggie Matsui
Content Developer, DataCamp
Jogando os dados

Jogando os dados
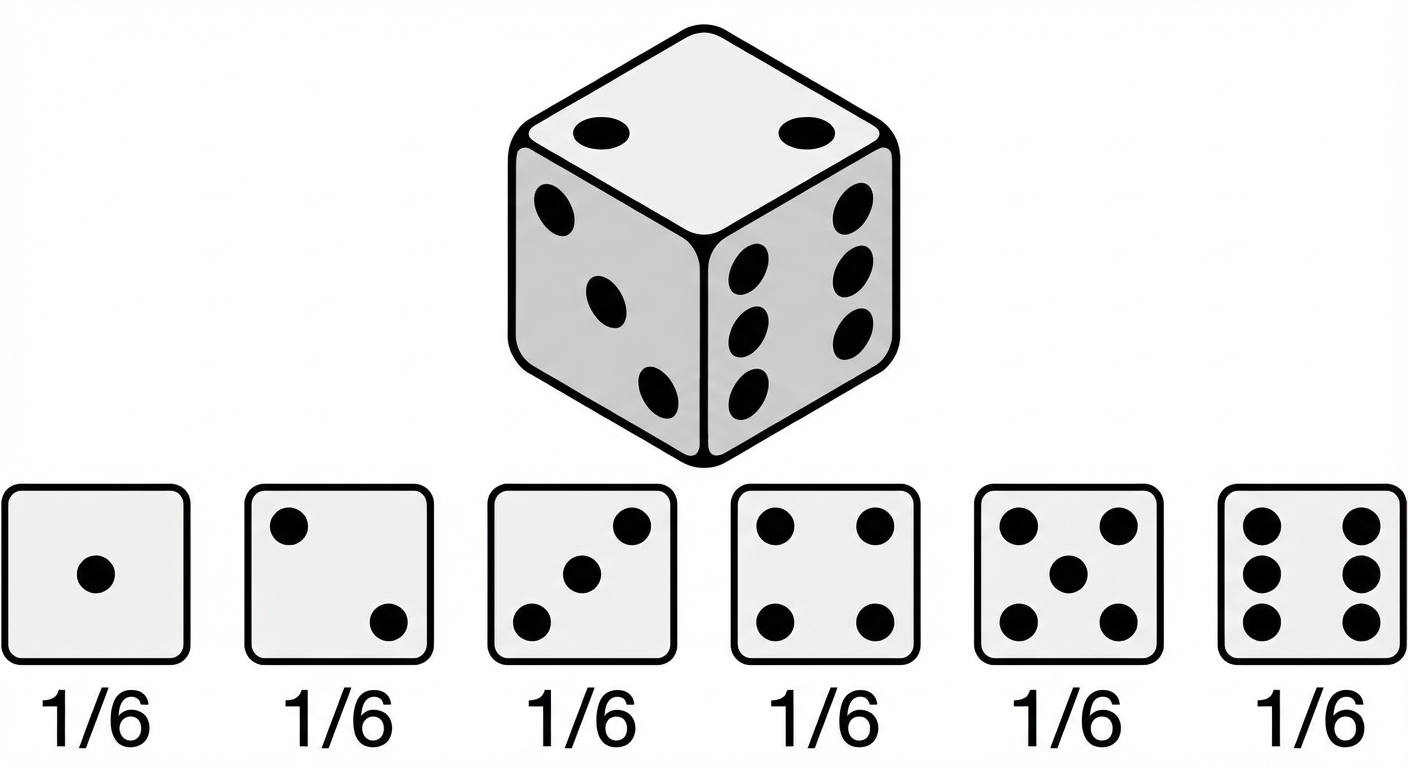
Escolha de vendedores
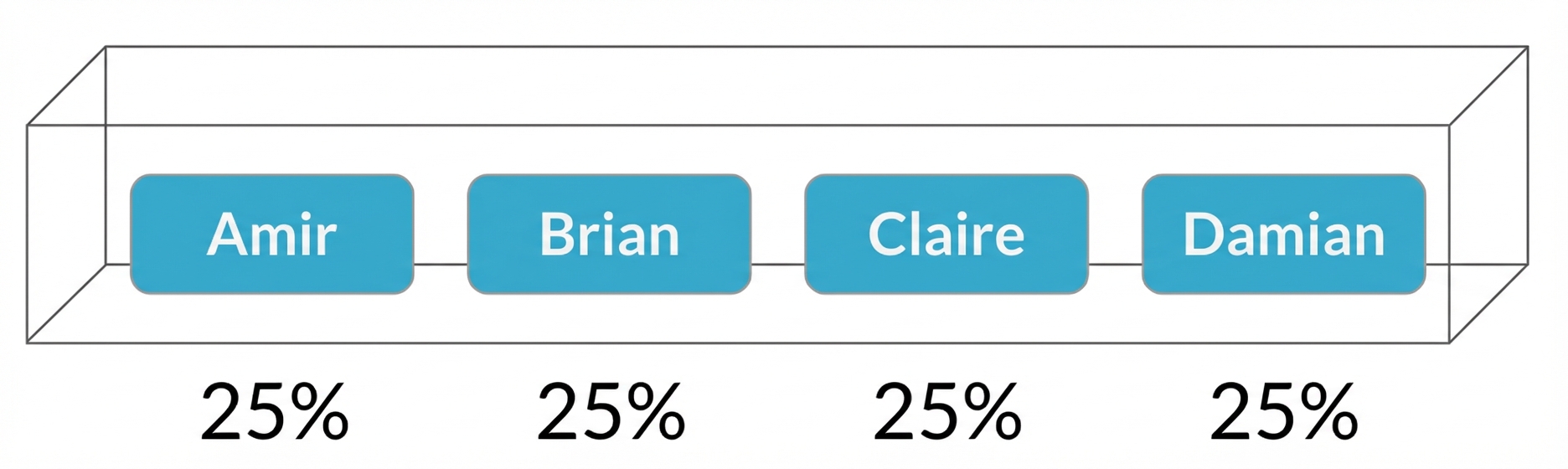
Distribuição de probabilidade
Descreve a probabilidade de cada resultado possível em um cenário

Valor esperado: média de uma distribuição de probabilidade
Valor esperado de um lançamento de dado justo = $(1 \times \frac{1}{6}) + (2 \times \frac{1}{6}) +(3 \times \frac{1}{6}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3.5$
Visualização de distribuição de probabilidade
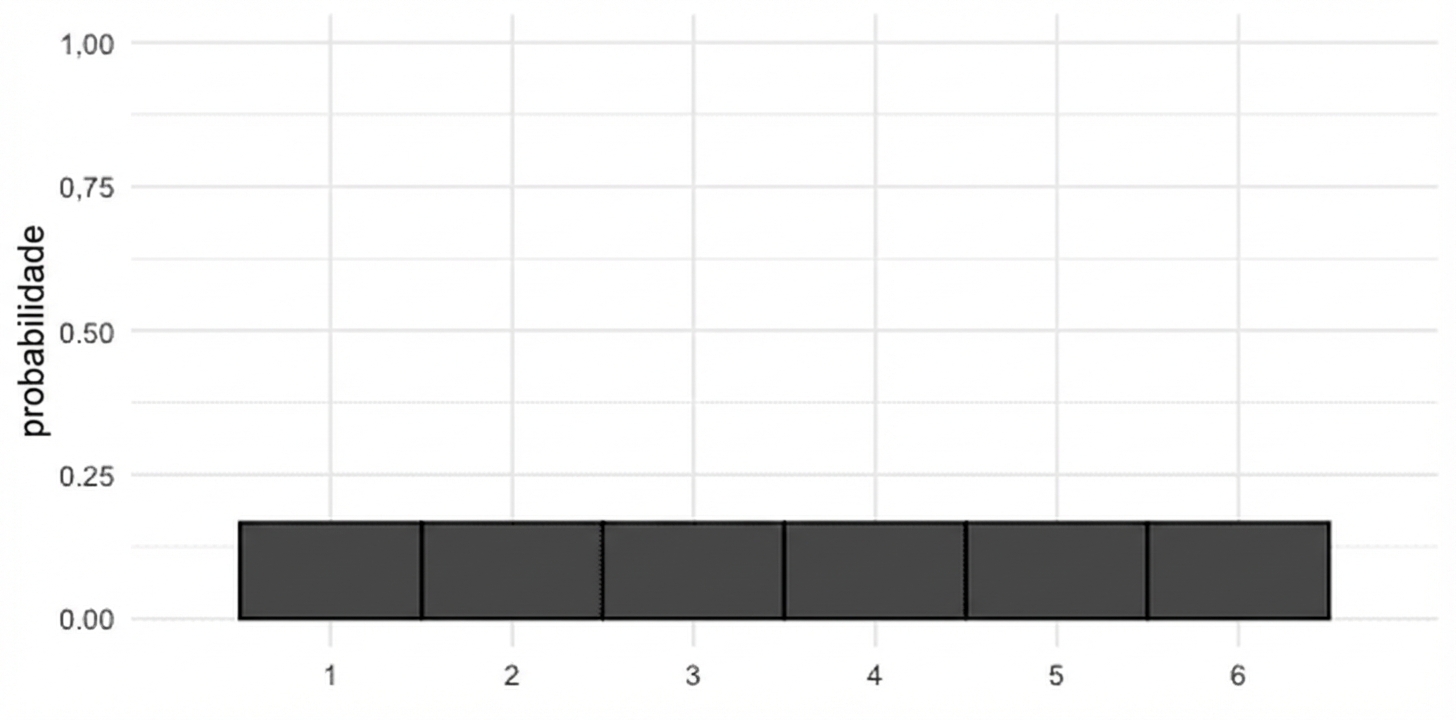
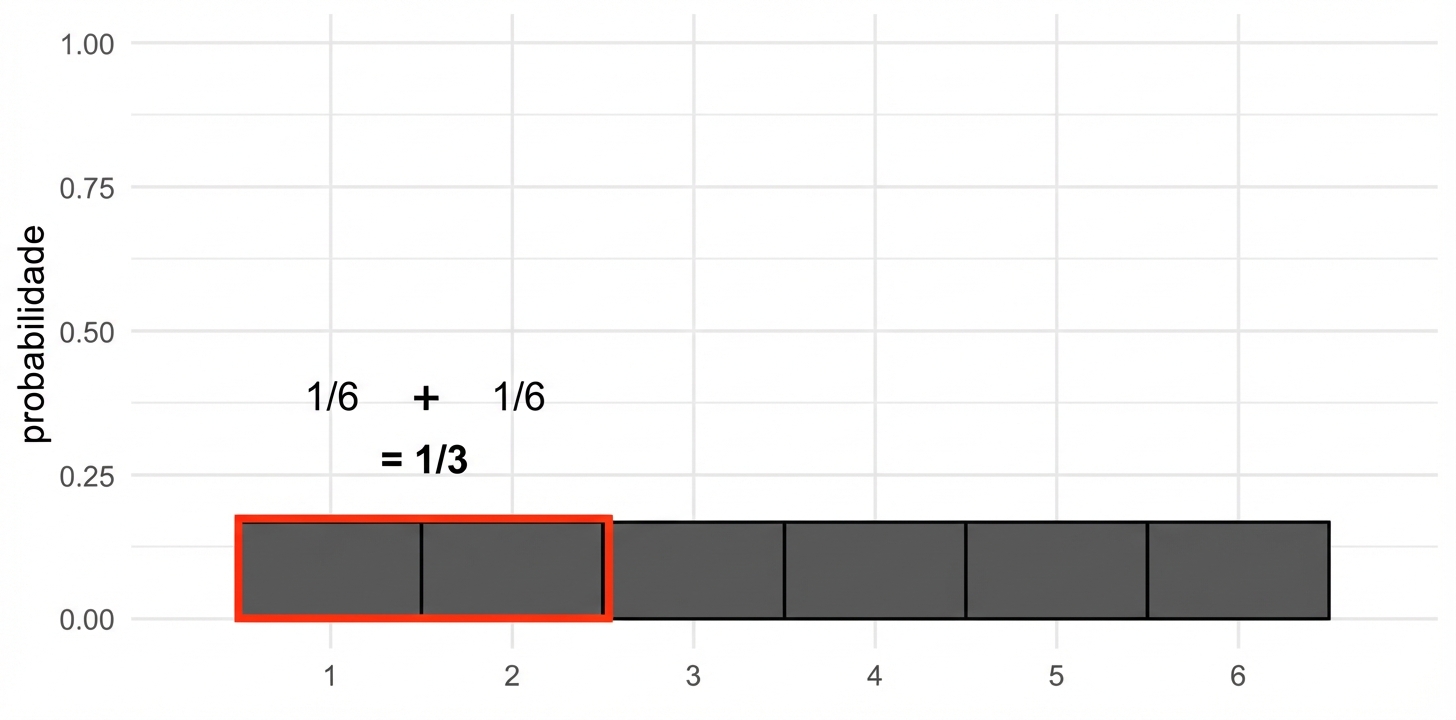
Probabilidade = área
$$P(\text{die roll}) \le 2 = ~?$$
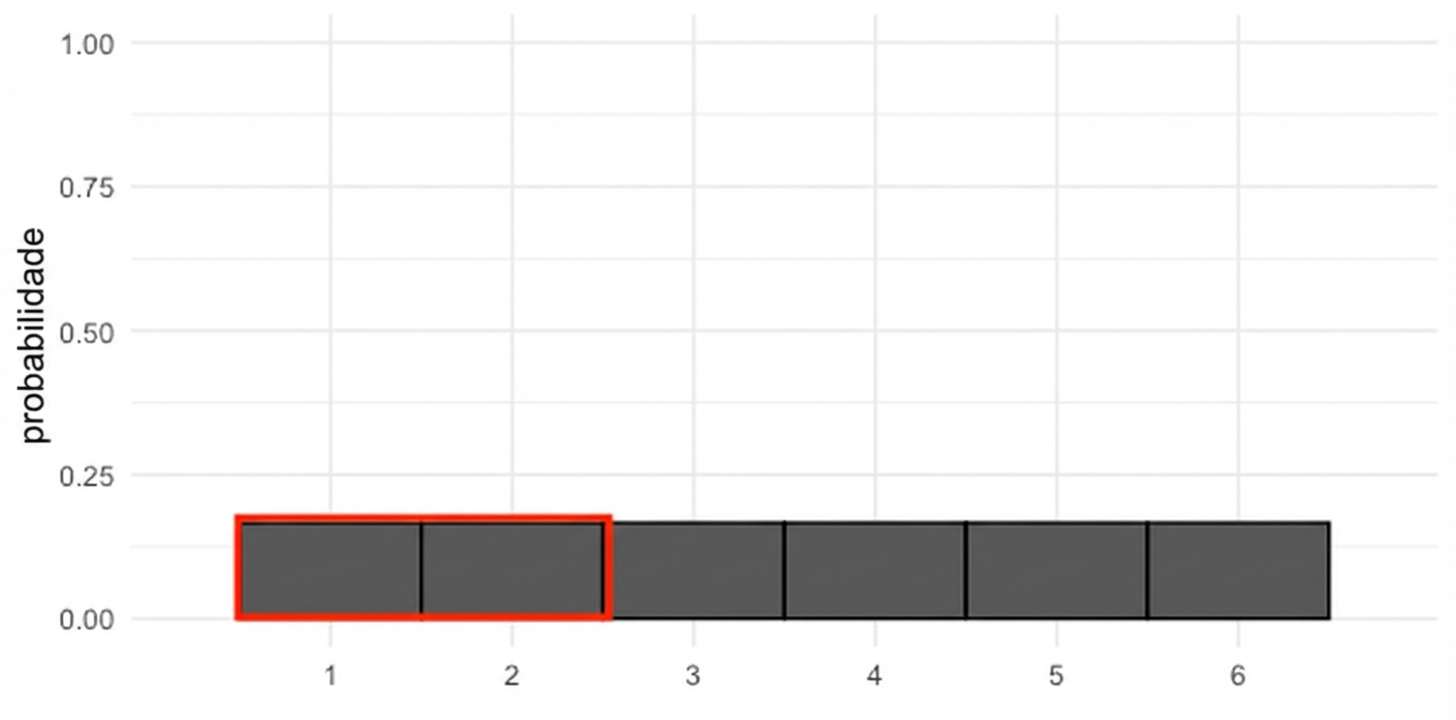
Probabilidade = área
$$P(\text{die roll}) \le 2 = 1/3$$
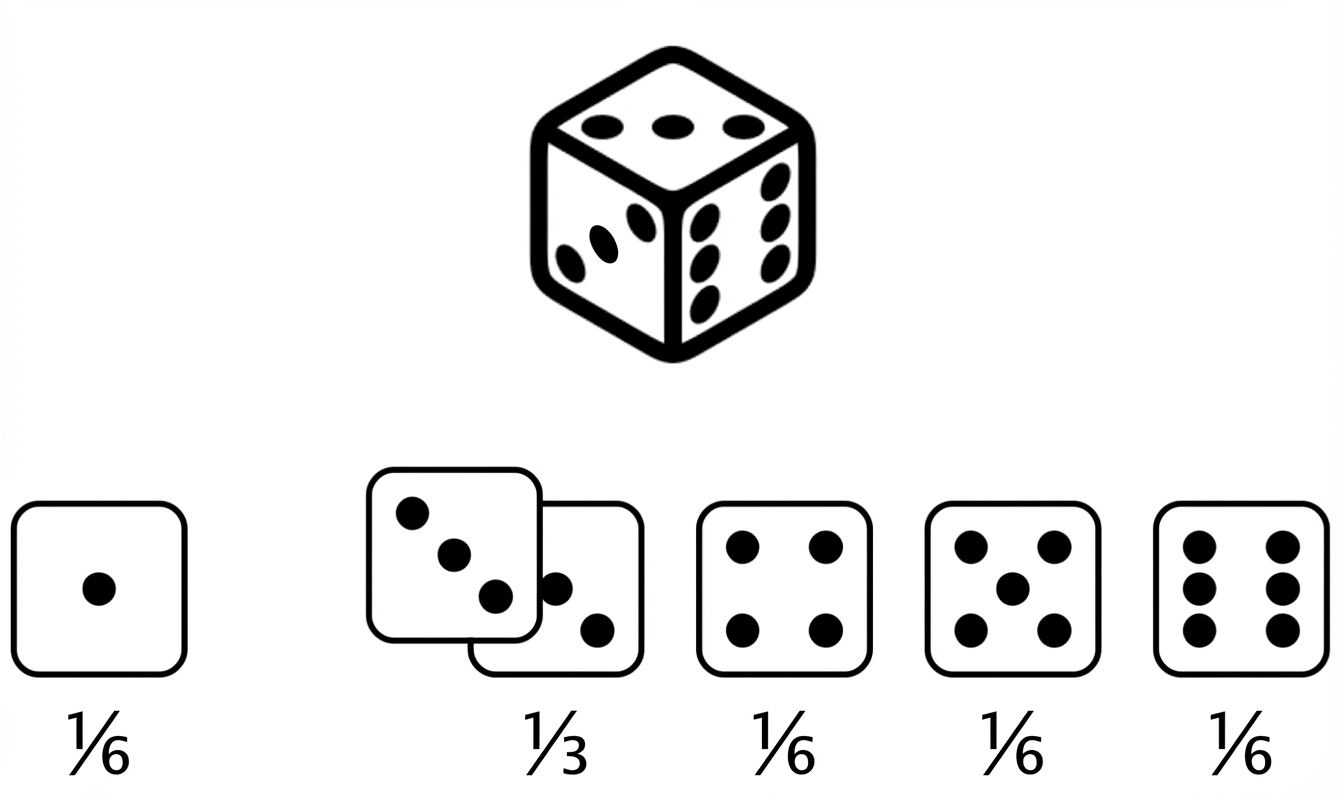
Dado viciado
Valor esperado do lançamento do dado viciado= $(1 \times \frac{1}{6}) +(2 \times 0) +(3 \times \frac{1}{3}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3.67$
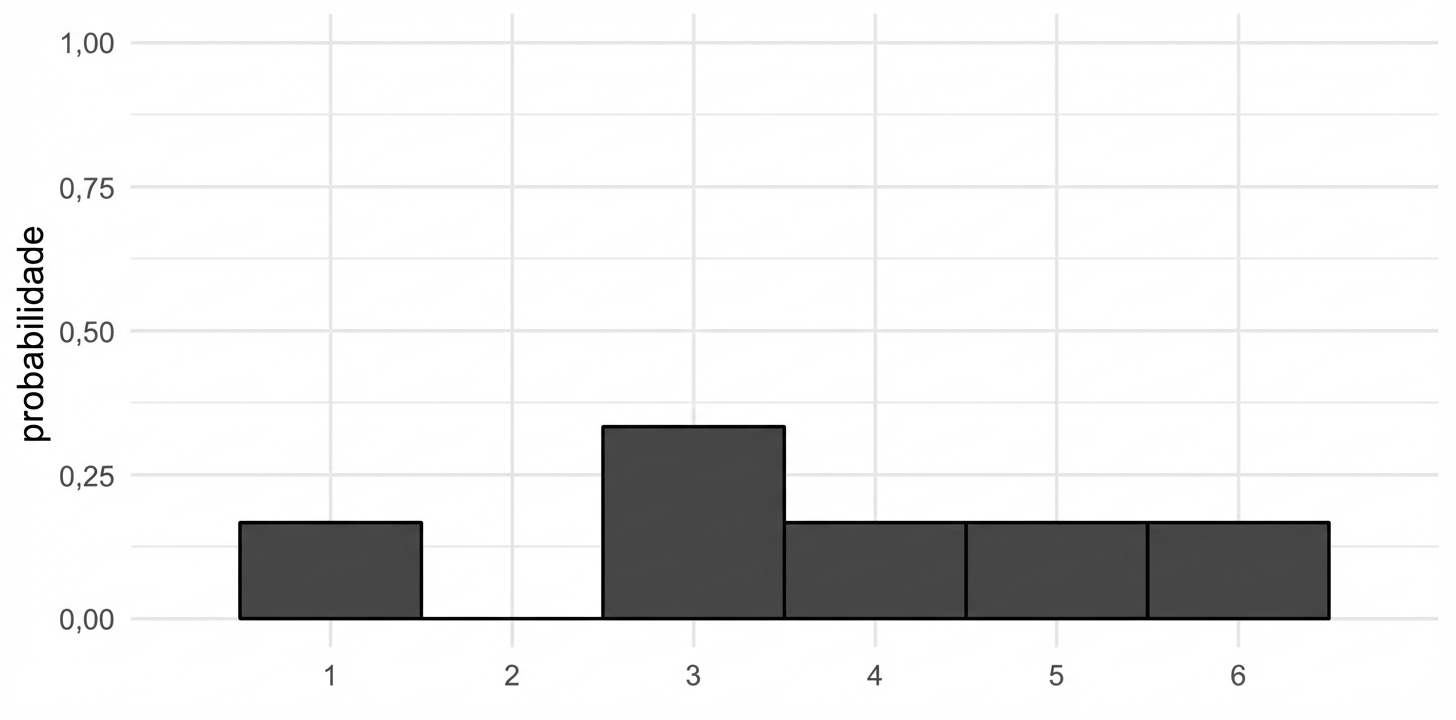
Visualização de probabilidades desiguais
Adicionar áreas
$$P(\text{uneven die roll}) \le 2 = ~?$$
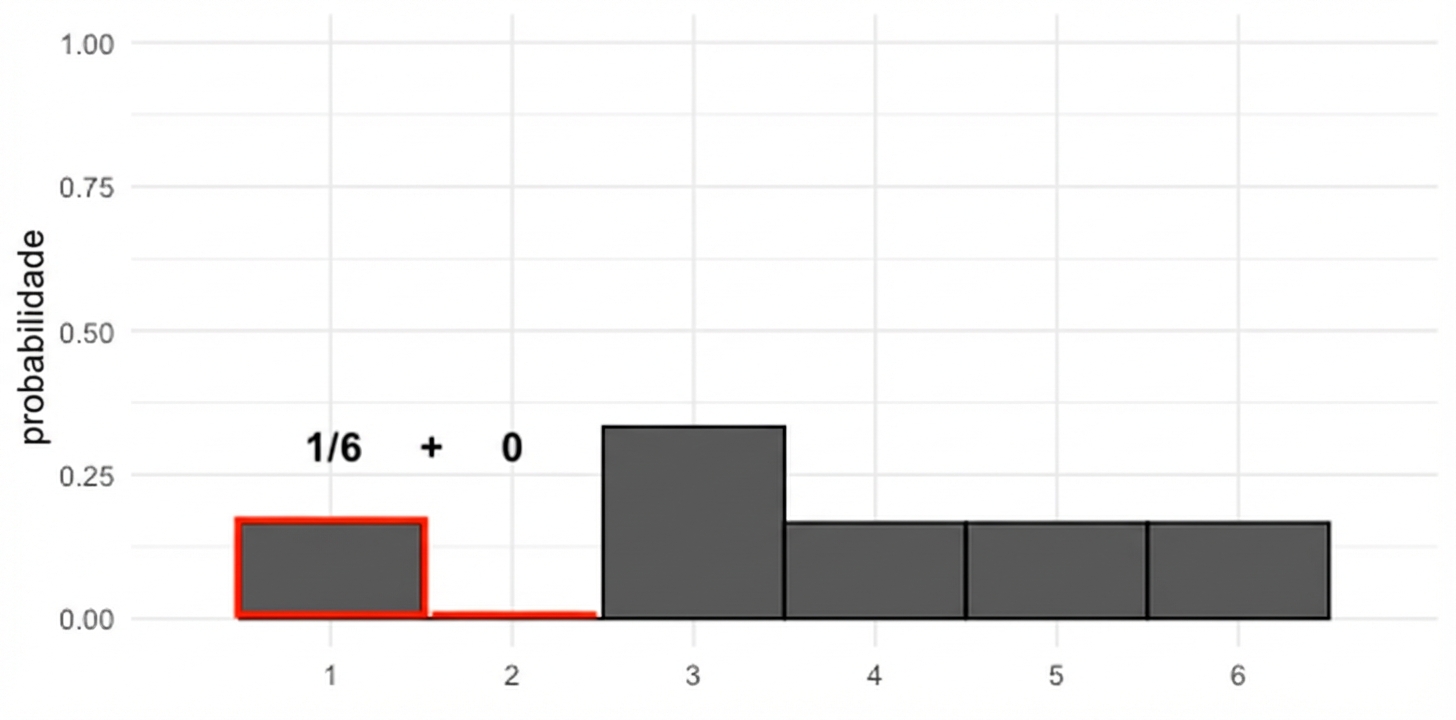
Adicionar áreas
$$P(\text{uneven die roll}) \le 2 = 1/6$$

Distribuições de probabilidade discretas
Descreva as probabilidades de resultados discretos
Dado justo

Distribuição uniforme discreta
Dado viciado

Amostragem de distribuições discretas
print(die)
number prob
0 1 0.166667
1 2 0.166667
2 3 0.166667
3 4 0.166667
4 5 0.166667
5 6 0.166667
np.mean(die['number'])
3.5
rolls_10 = die.sample(10, replace = True)
rolls_10
number prob
0 1 0.166667
0 1 0.166667
4 5 0.166667
1 2 0.166667
0 1 0.166667
0 1 0.166667
5 6 0.166667
5 6 0.166667
...
Visualização de amostra
rolls_10['number'].hist(bins=np.linspace(1,7,7))
plt.show()
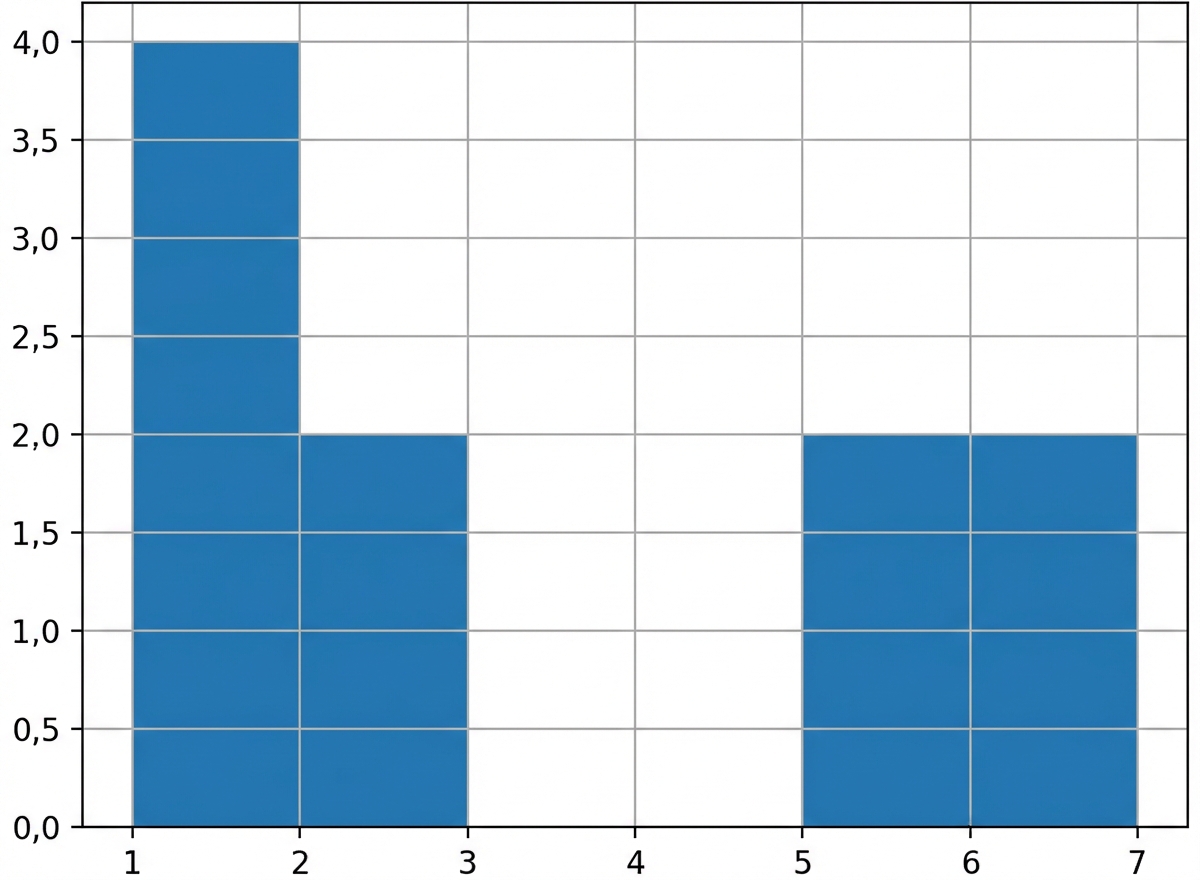
Distribuição de amostra vs. distribuição teórica
Amostra de 10 jogadas

np.mean(rolls_10['number']) = 3.0
Distribuição teórica de probabilidade
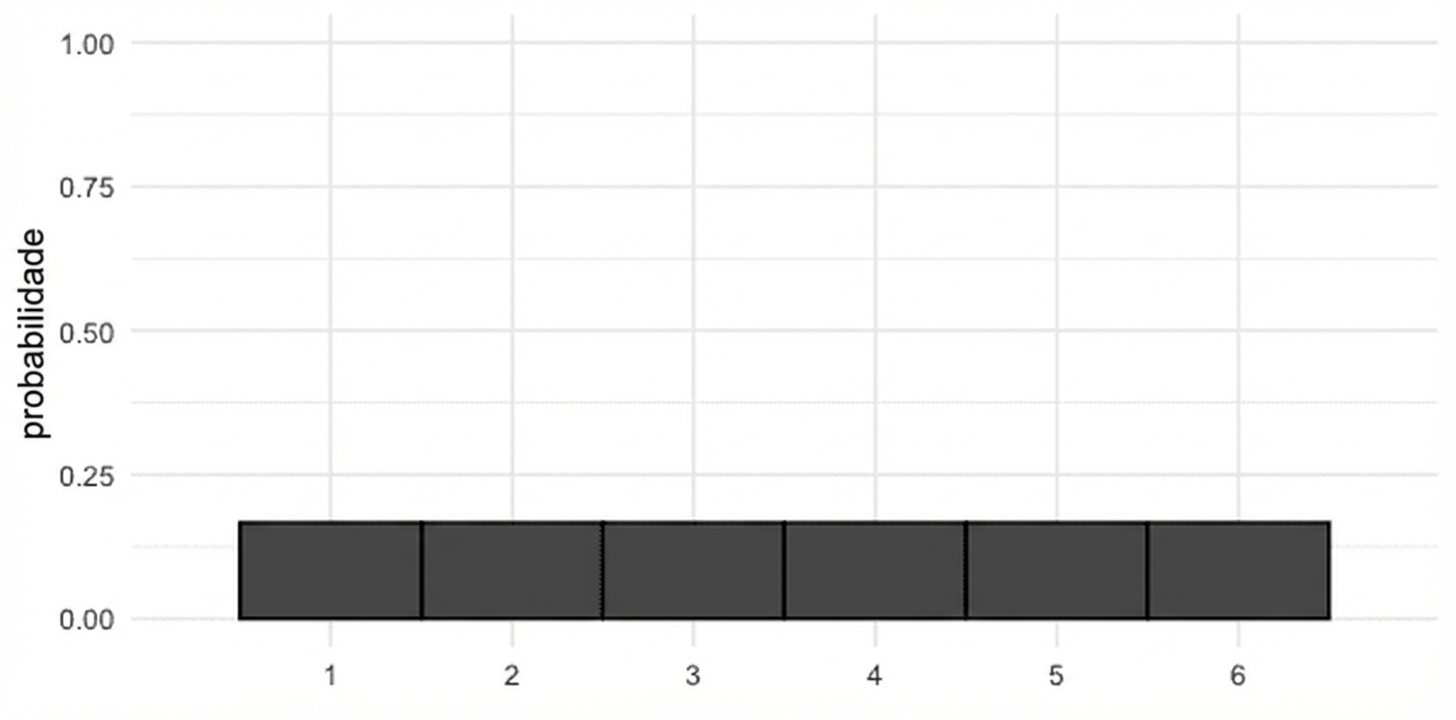
mean(die['number']) = 3.5
Uma amostra maior
Amostra de 100 jogadas
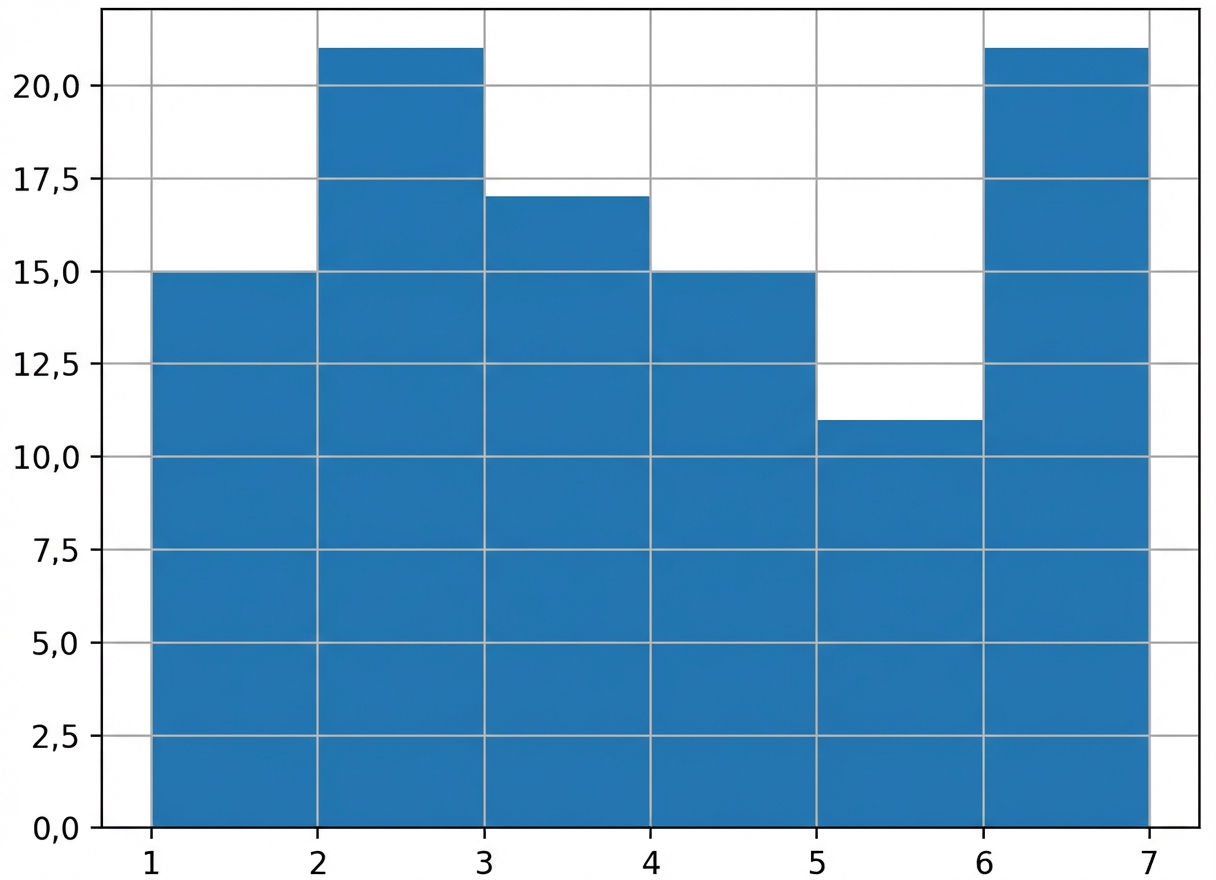
np.mean(rolls_100['number']) = 3.4
Distribuição teórica de probabilidade

mean(die['number']) = 3.5
Uma amostra ainda maior
Amostra de 1.000 jogadas
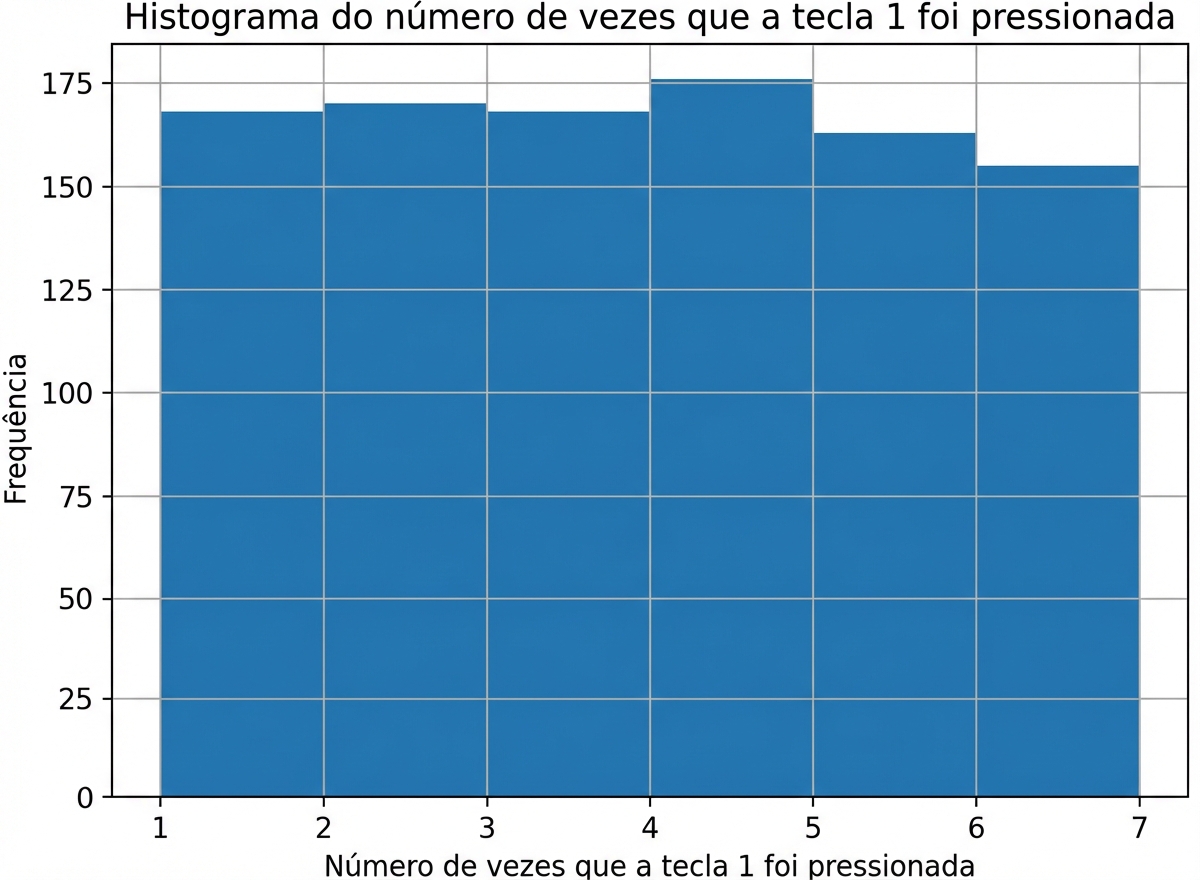
np.mean(rolls_1000['number']) = 3.48
Distribuição teórica de probabilidade

mean(die['number']) = 3.5
Lei dos grandes números
À medida que o tamanho da sua amostra aumenta, a média da amostra se aproximará do valor esperado.
| Tamanho da amostra | Média |
|---|---|
| 10 | 3,00 |
| 100 | 3,40 |
| 1000 | 3,48 |
Vamos praticar!
Introdução à estatística em Python

