Correlação
Introdução à estatística em Python

Maggie Matsui
Content Developer, DataCamp
Relações entre duas variáveis
- x = variável explicativa/independente
- y = variável de resposta/dependente
Coeficiente de correlação
- Quantifica a relação linear entre duas variáveis
- Número entre -1 e 1
- A magnitude corresponde à força da relação
- O sinal (+ ou -) corresponde à direção da relação
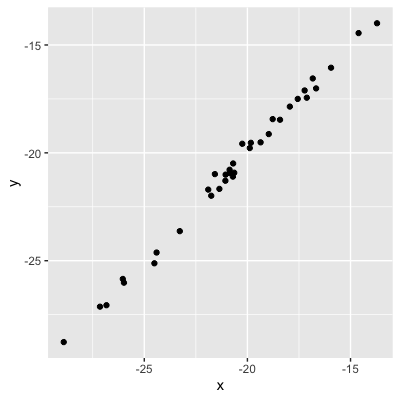
Magnitude = força da relação
0,99 (relacionamento muito forte)
Magnitude = força da relação
0,99 (relacionamento muito forte)

0,75 (relação forte)
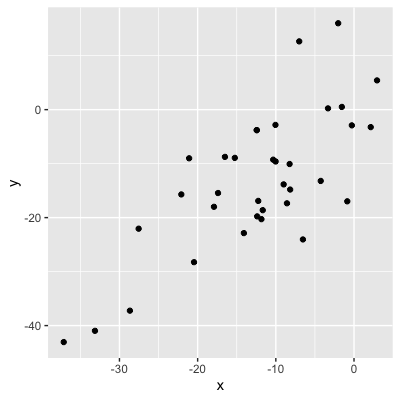
Magnitude = força da relação
0,56 (relação moderada)
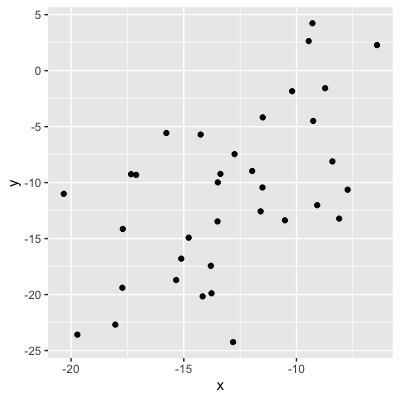
Magnitude = força da relação
0,56 (relação moderada)

0,21 (relação fraca)
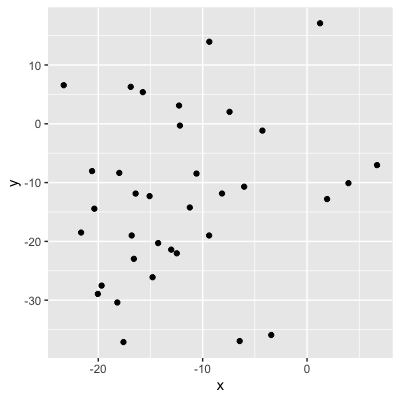
Magnitude = força da relação
0,04 (sem relação)
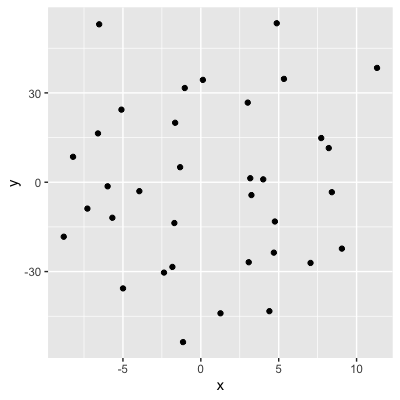
- Saber o valor de
xnão nos diz nada sobrey
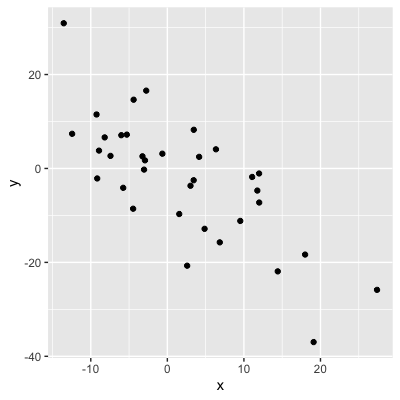
Sinal = direção
0,75: conforme x aumenta, y aumenta

-0,75: conforme x aumenta, y diminui
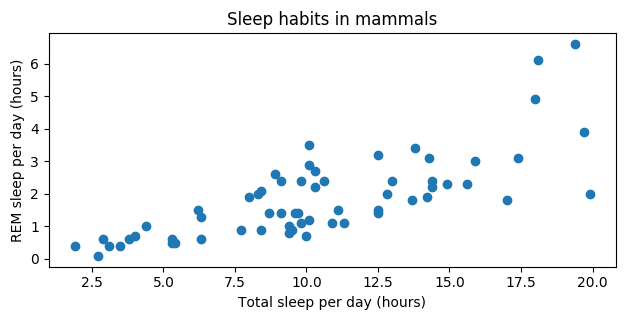
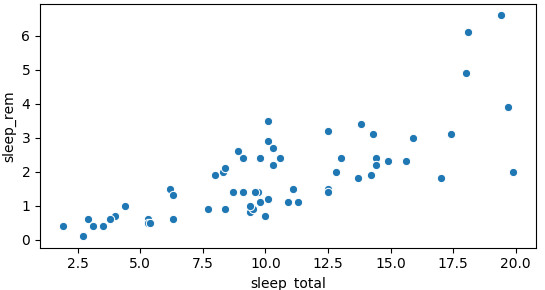
Visualização de relacionamentos
import seaborn as snssns.scatterplot(x="sleep_total", y="sleep_rem", data=msleep)plt.show()
Adicionar uma linha de tendência
import seaborn as sns sns.lmplot(x="sleep_total", y="sleep_rem", data=msleep, ci=None)plt.show()
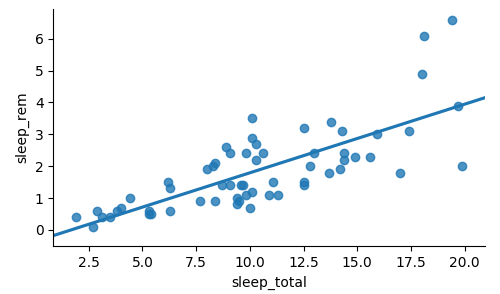
Correlação de computação
msleep['sleep_total'].corr(msleep['sleep_rem'])
0.751755
msleep['sleep_rem'].corr(msleep['sleep_total'])
0.751755
Muitas maneiras de calcular a correlação
- Usado neste curso: coeficiente de correlação de Pearson ($r$)
- Mais comum
- $\bar{x} =$ média de $x$
- $\sigma_x =$ desvio padrão de $x$
$$ r = \frac{1}{n - 1} \sum_{i=1}^{n} \frac{(x_i - \bar{x})(y_i - \bar{y})}{\sigma_x \cdot \sigma_y}$$
- Variações dessa fórmula:
- Tau de Kendall
- Rho de Spearman
Vamos praticar!
Introdução à estatística em Python

