Correlation
Introdução à estatística

George Boorman
Curriculum Manager, DataCamp
Relationships between two variables
Pearson correlation coefficient
- Published by Karl Pearson in 1896!
- Quantifies the strength of a relationship between two variables
- Number between minus one and one
- Magnitude corresponds to strength of relationship
- Sign (+ or -) corresponds to direction of relationship
1 https://royalsocietypublishing.org/doi/10.1098/rsta.1896.0007
Linear relationships
- Linear = proportionate changes between dependent and independent variables
Values = strength of the relationship
0.99 (very strong relationship)
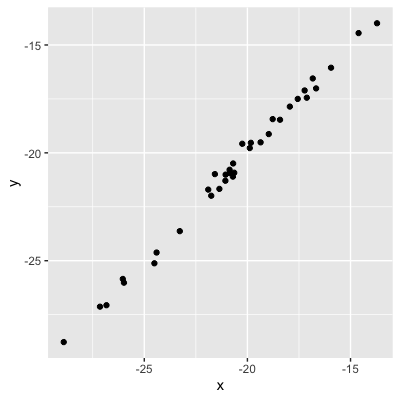
Values = strength of the relationship
0.99 (very strong relationship)

0.75 (strong relationship)
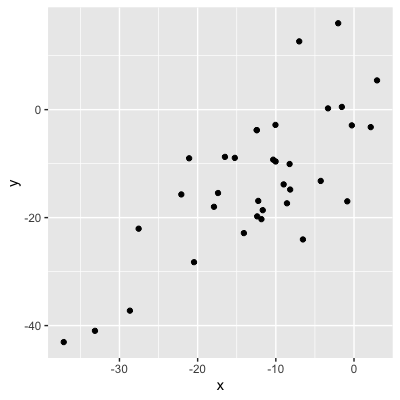
Values = strength of the relationship
0.56 (moderate relationship)
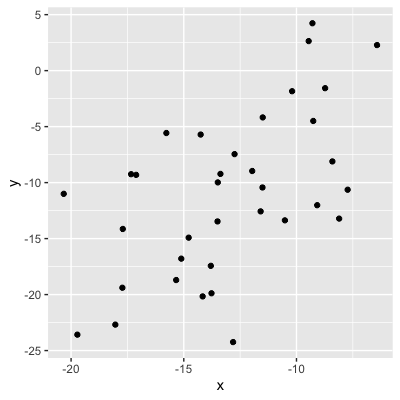
Values = strength of the relationship
0.56 (moderate relationship)

0.21 (weak relationship)
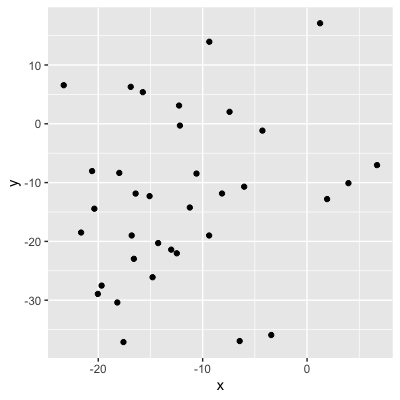
Values = strength of the relationship
0.04 (no relationship)
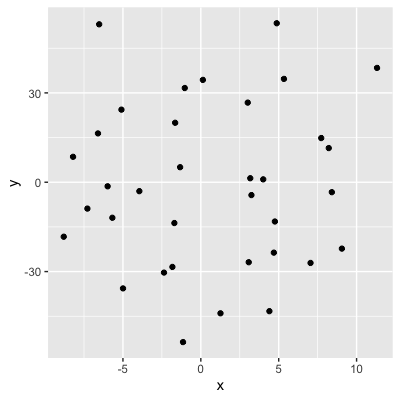
- Knowing the value of x doesn't tell us anything about y
Sign = direction
0.75: as x increases, y increases

-0.75: as x increases, y decreases
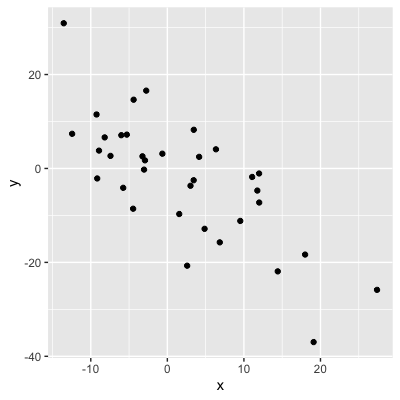
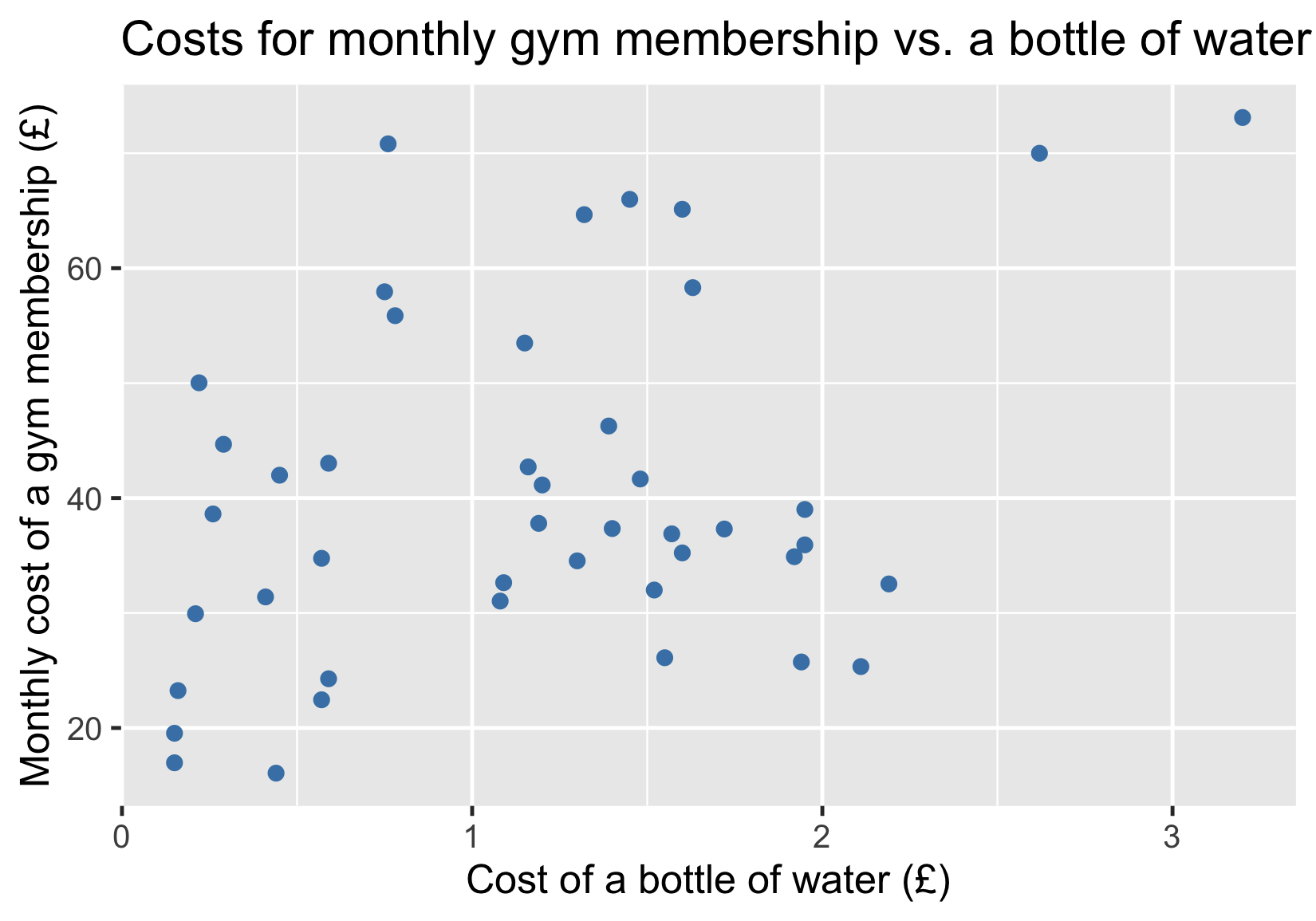
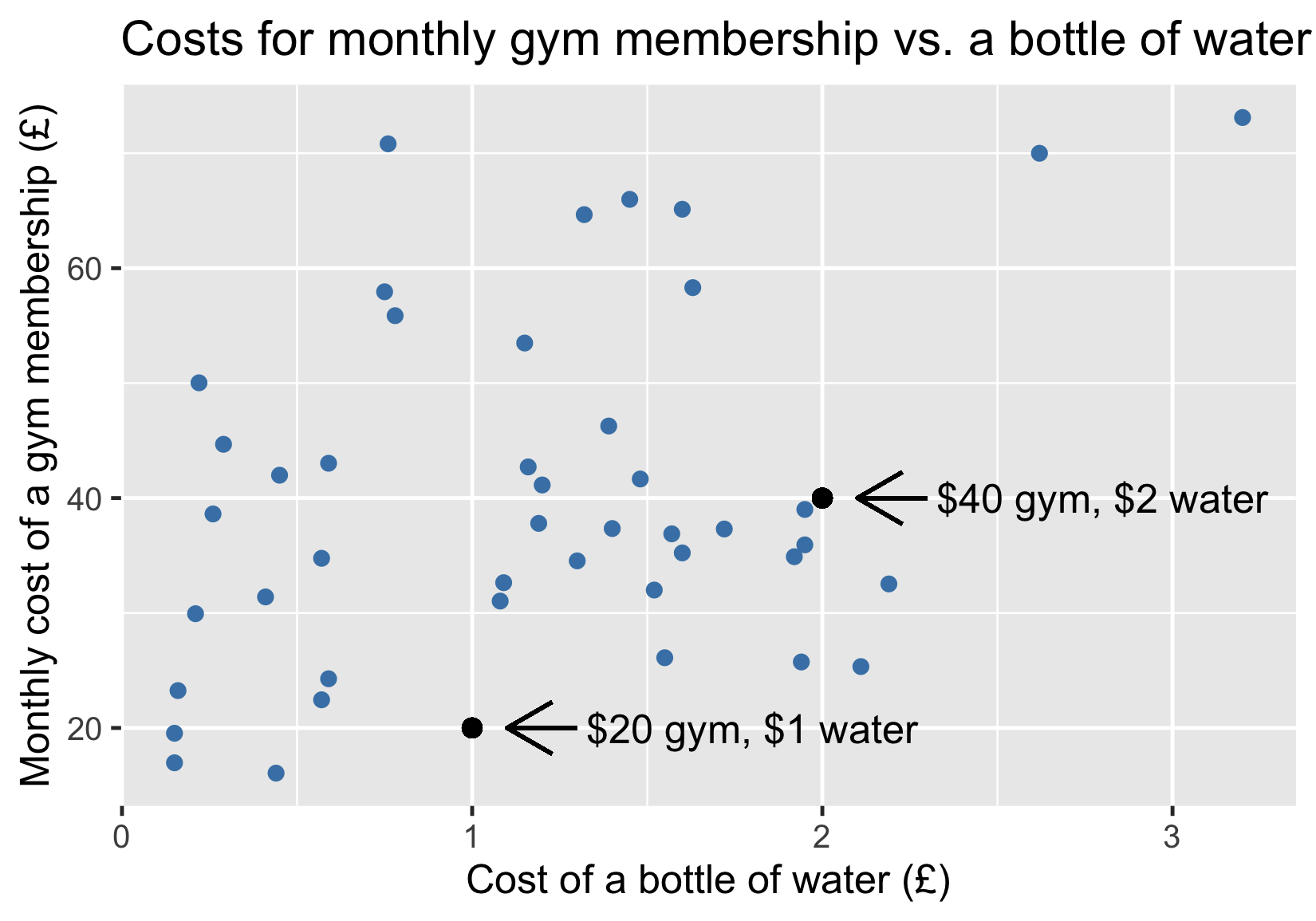
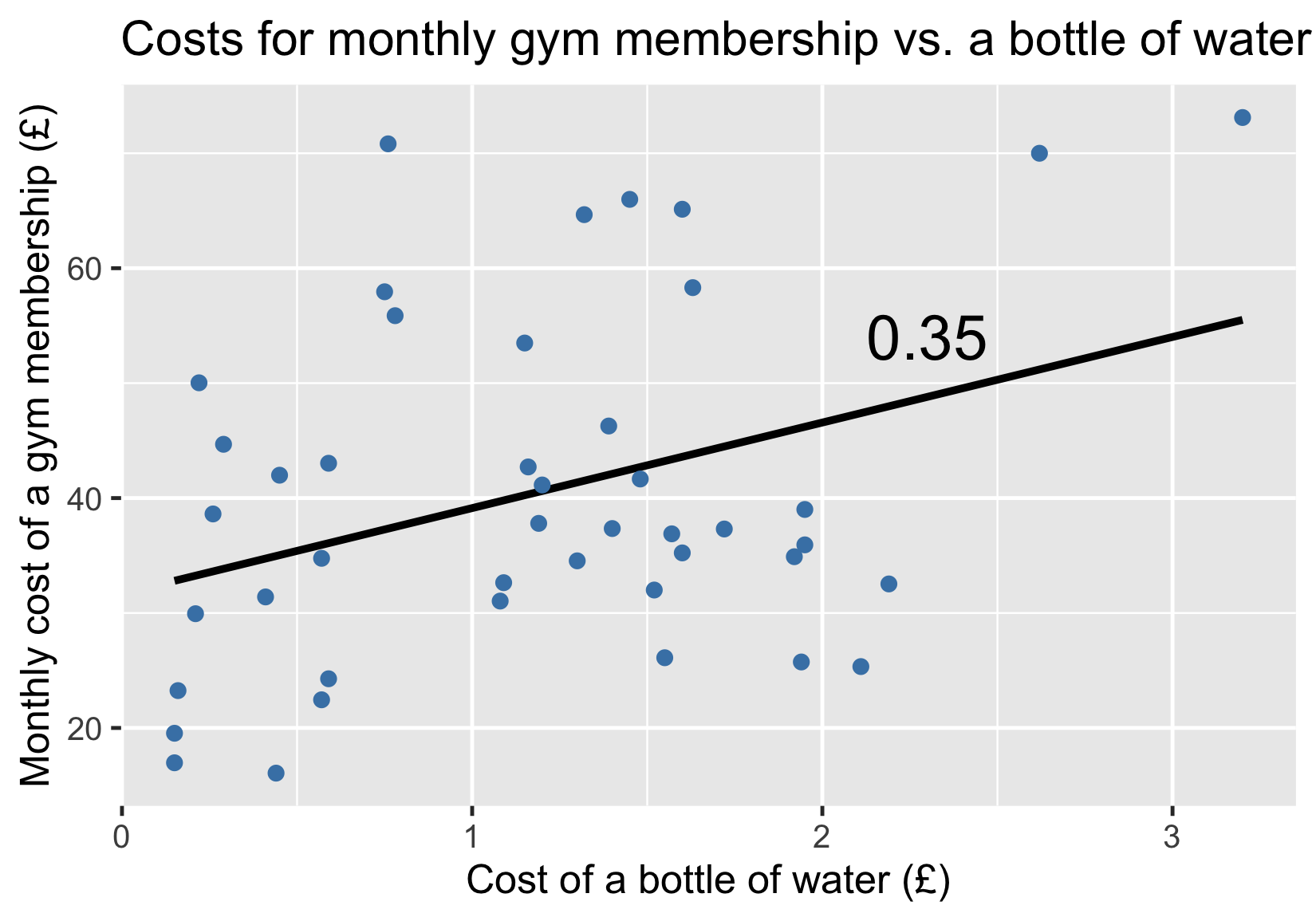
Gym costs vs. water costs

Adding a trendline
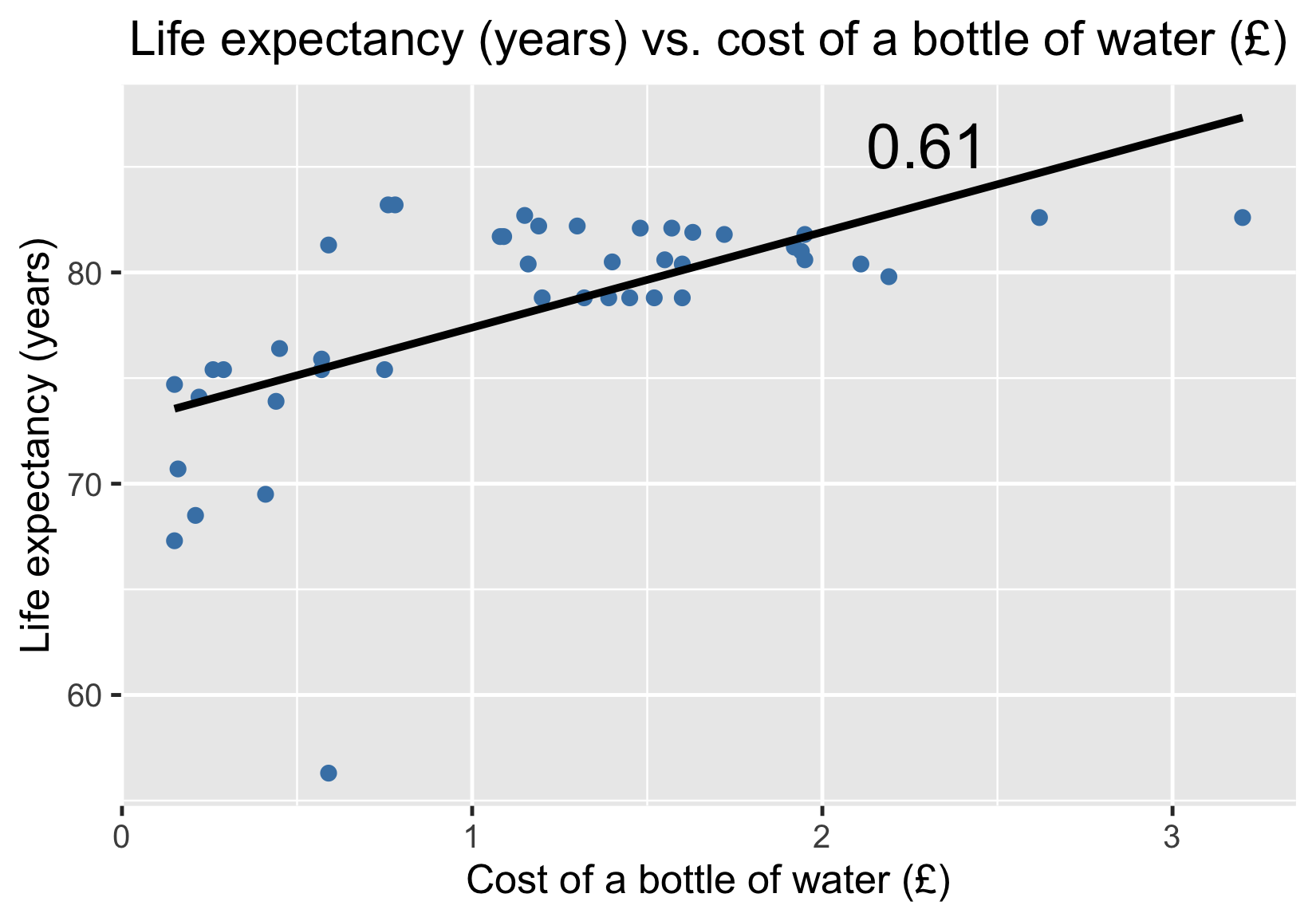
Life expectancy vs. cost of a bottle of water
Correlation does not equal causation
- Will increasing the cost of water result in an increase in life expectancy?


- Correlation does not equal causation
1 Image credit: https://unsplash.com/@micheile; https://unsplash.com/@jon_chng
Confounding variables
What else might be affecting life expectancy?
- A bottle of water costs more in countries with strong economies
- These countries generally offer access to high-quality healthcare
The strength of the economy could be a confounding variable
- A confounding variable is not measured, but may affect the relationship between our variables

Let's practice!
Introdução à estatística

