Korrelation
Einführung in die Statistik

George Boorman
Curriculum Manager, DataCamp
Korrelation zwischen zwei Variablen
Pearson-Korrelationskoeffizient
- Veröffentlicht von Karl Pearson im Jahr 1896!
- Quantifiziert die Stärke einer Korrelation zwischen zwei Variablen
- Zahl zwischen minus eins und eins
- Die Größe entspricht der Stärke der Korrelation
- Das Vorzeichen (+ oder -) entspricht der Richtung der Korrelation
1 https://royalsocietypublishing.org/doi/10.1098/rsta.1896.0007
Lineare Korrelationen
- Linear = proportionale Veränderungen zwischen abhängigen und unabhängigen Variablen
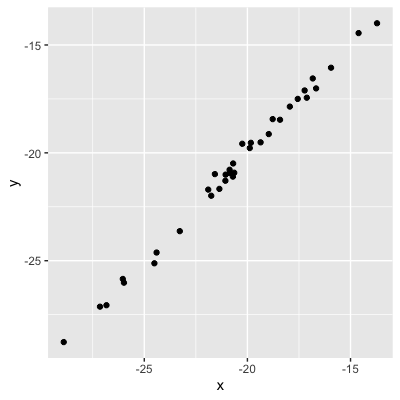
Werte = Stärke der Korrelation
0,99 (sehr starke Korrelation)
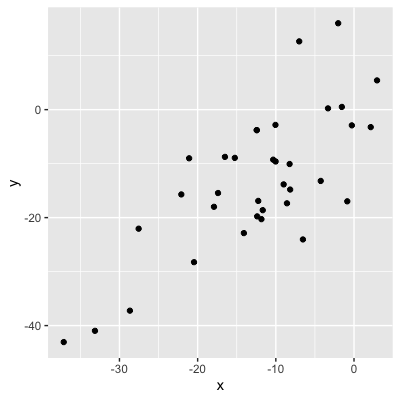
Werte = Stärke der Korrelation
0,99 (sehr starke Korrelation)

0,75 (starke Korrelation)
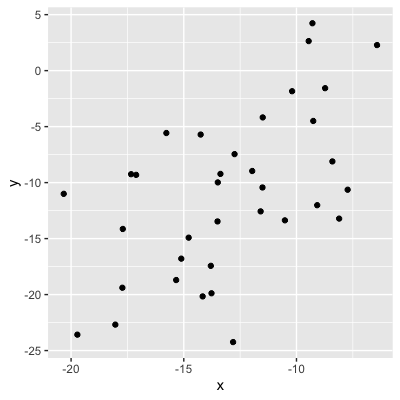
Werte = Stärke der Korrelation
0,56 (moderate Beziehung)
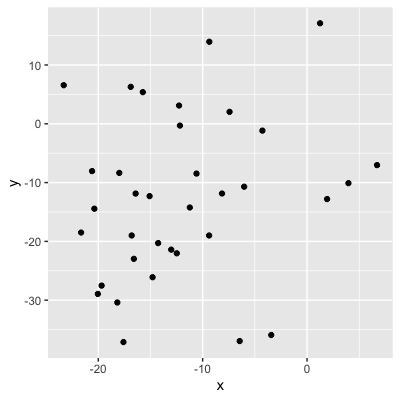
Werte = Stärke der Korrelation
0,56 (moderate Beziehung)

0,21 (schwache Korrelation)
Werte = Stärke der Korrelation
0,04 (keine Korrelation)
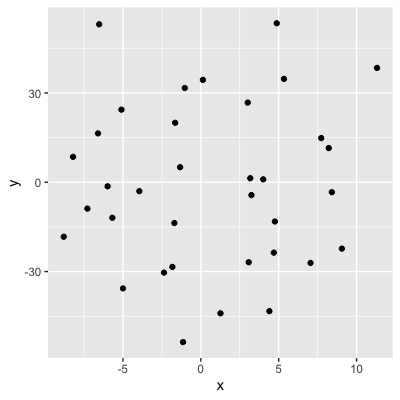
- Der Wert von x sagt nichts über y aus
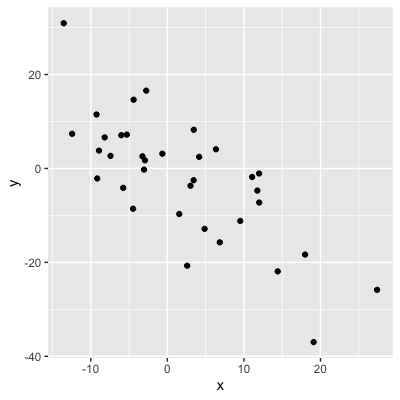
Vorzeichen = Richtung
0,75: Wenn x steigt, steigt y

-0,75: Wenn x steigt, sinkt y
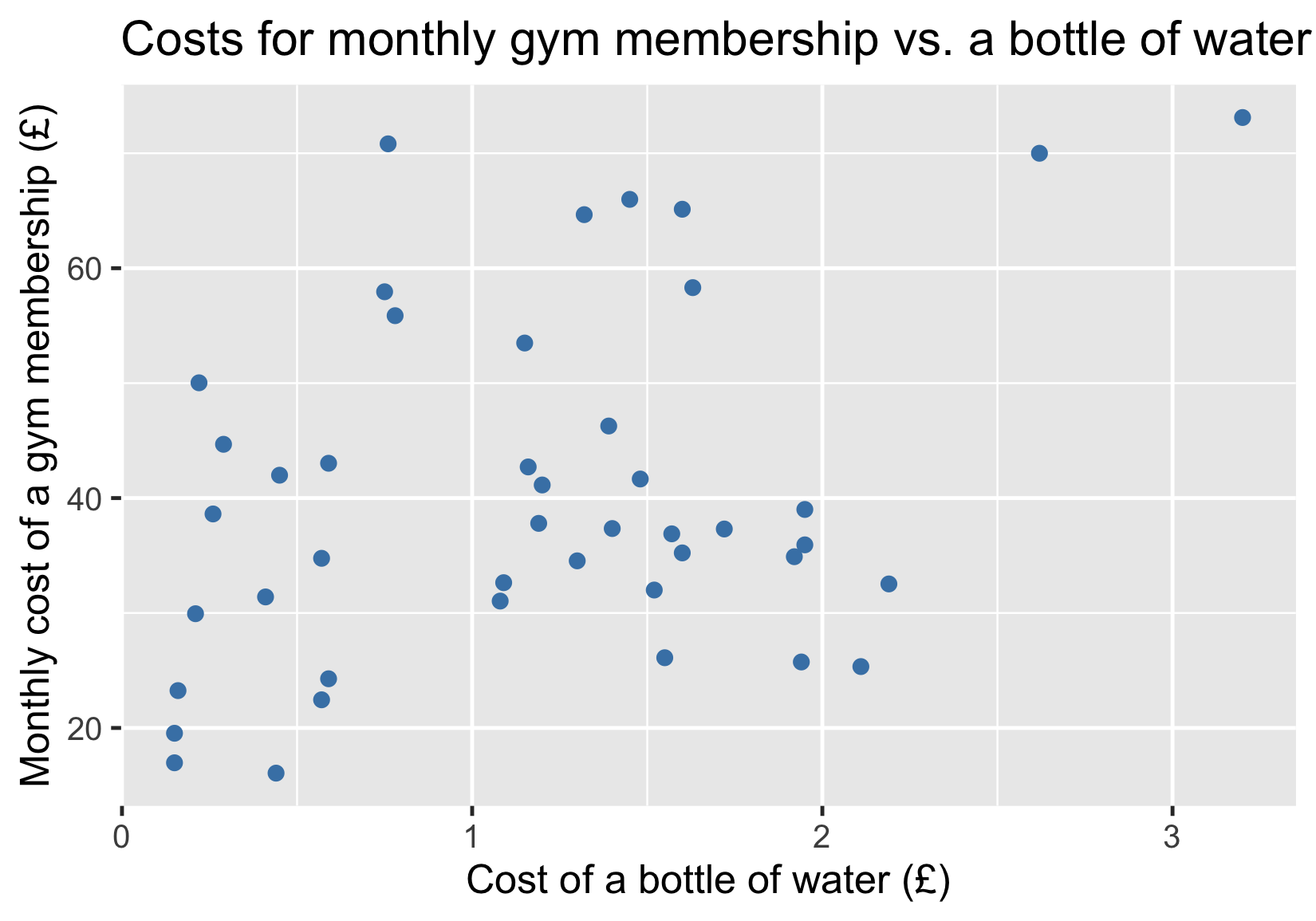
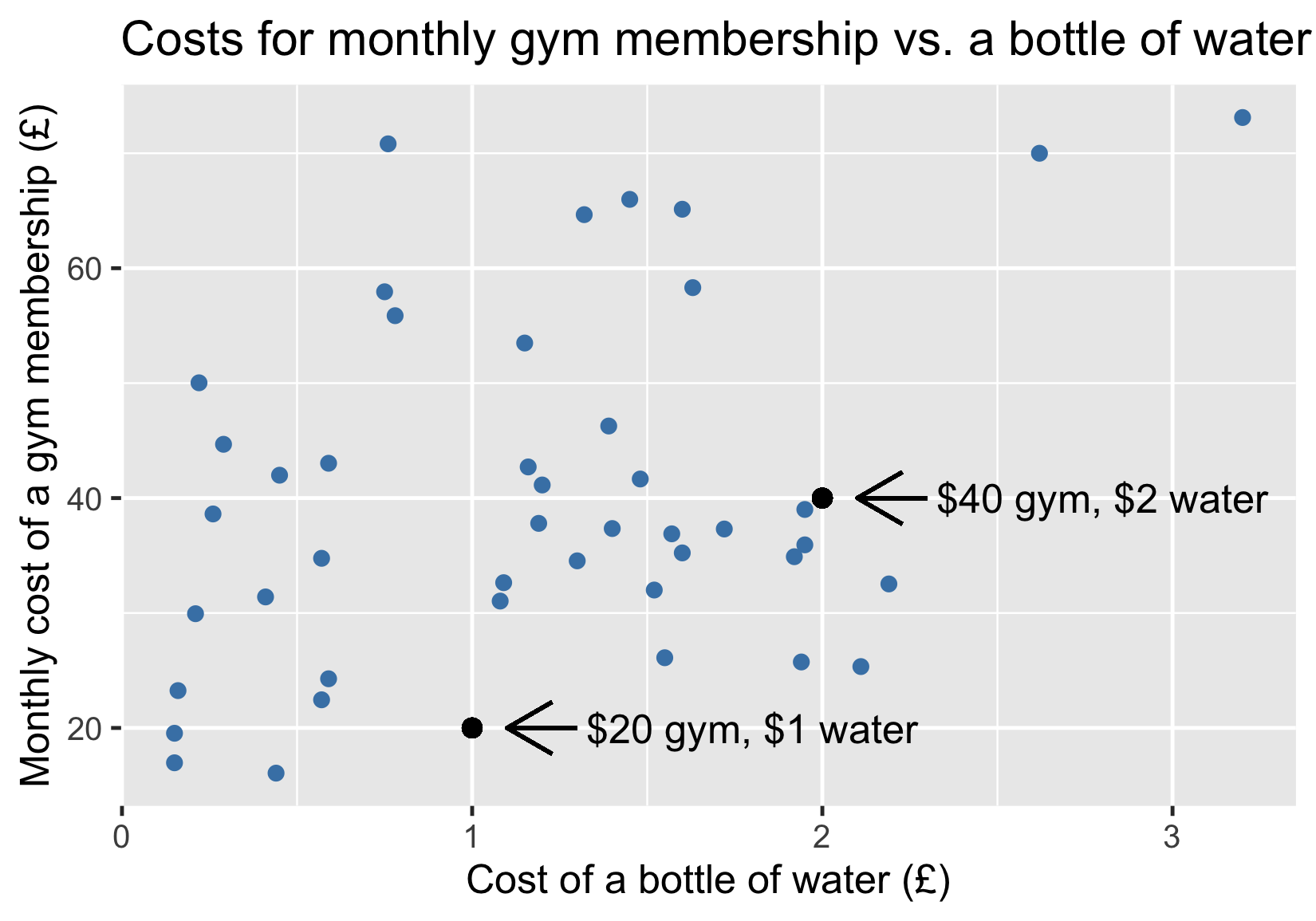
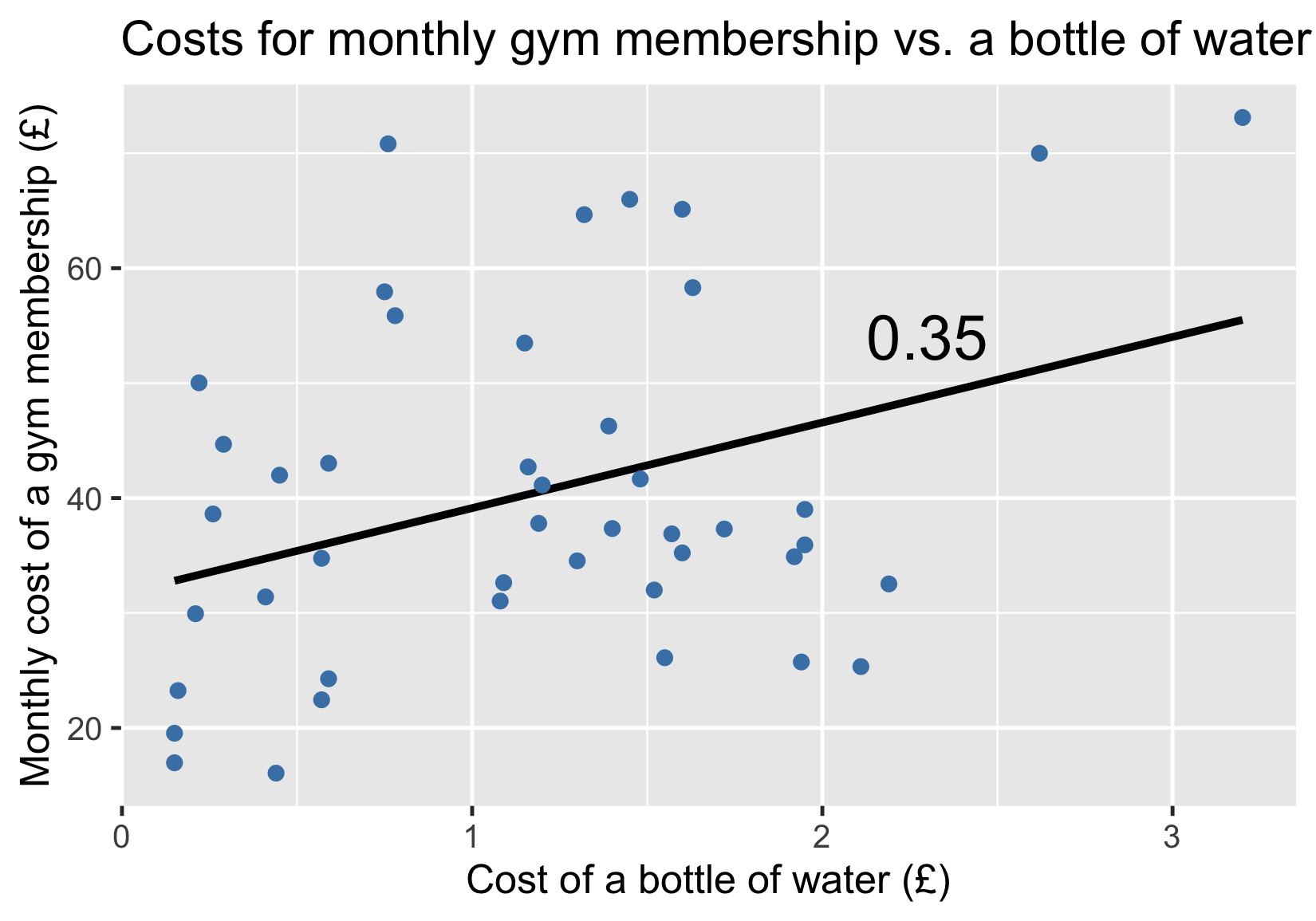
Fitnessstudiokosten vs. Wasserkosten

Hinzufügen einer Trendlinie
Lebenserwartung vs. Kosten für eine Flasche Wasser
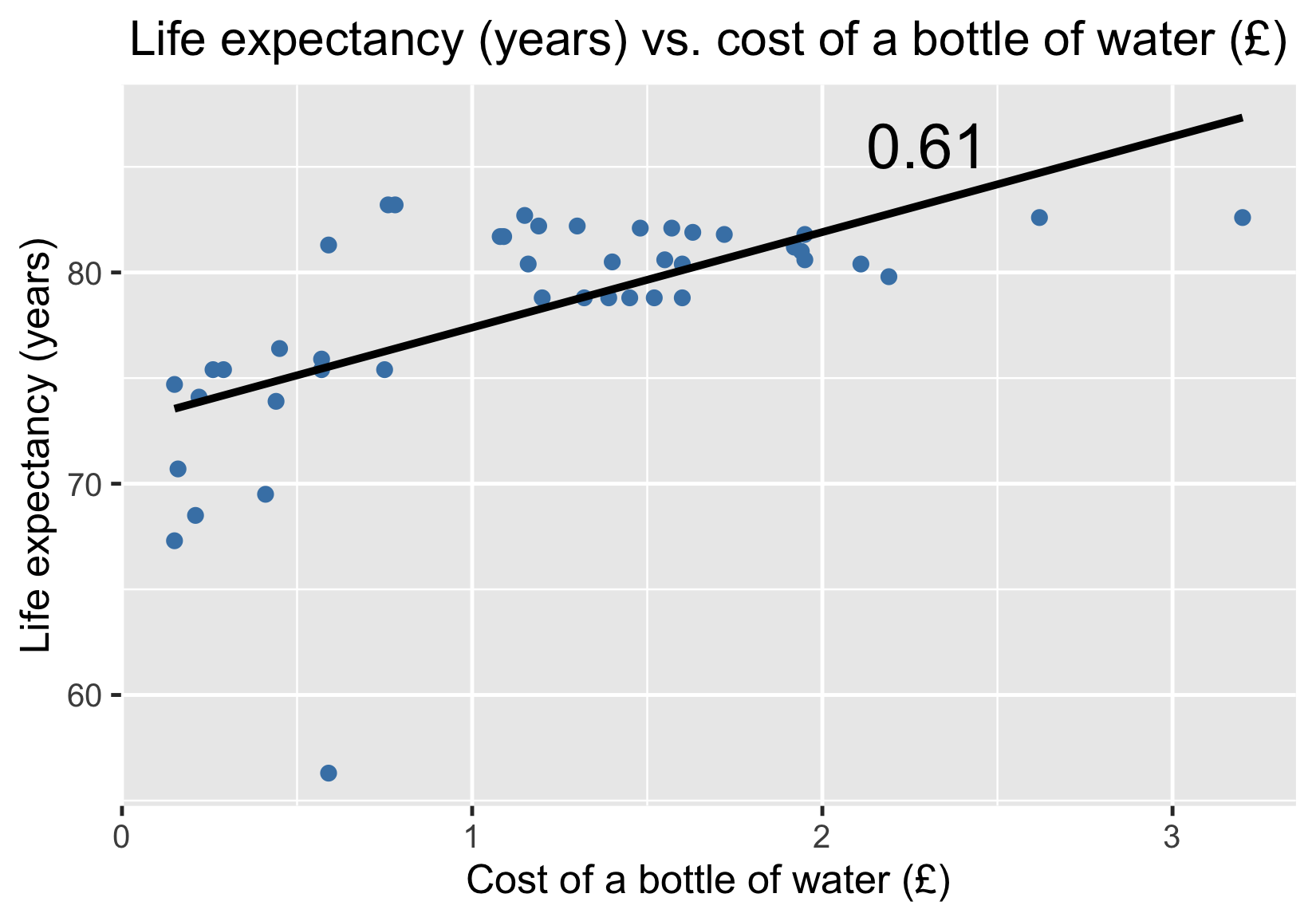
Korrelation ist nicht gleich Kausalität
- Führt eine Erhöhung der Wasserkosten zu einem Anstieg der Lebenserwartung?


- Korrelation ist nicht gleich Kausalität
1 Bildnachweis: https://unsplash.com/@micheile; https://unsplash.com/@jon_chng
Störvariablen
Was könnte die Lebenserwartung noch beeinflussen?
- Eine Flasche Wasser kostet mehr in Ländern mit starker Wirtschaft
- Diese Länder bieten im Allgemeinen Zugang zu einer hochwertigen Gesundheitsversorgung
Die Stärke der Wirtschaft könnte eine Störvariable sein
- Eine Störvariable wird nicht gemessen, kann aber die Beziehung zwischen anderen Variablen beeinflussen

Lass uns üben!
Einführung in die Statistik

