Die Binomialverteilung
Einführung in die Statistik

George Boorman
Curriculum Manager, DataCamp
Der Münzwurf
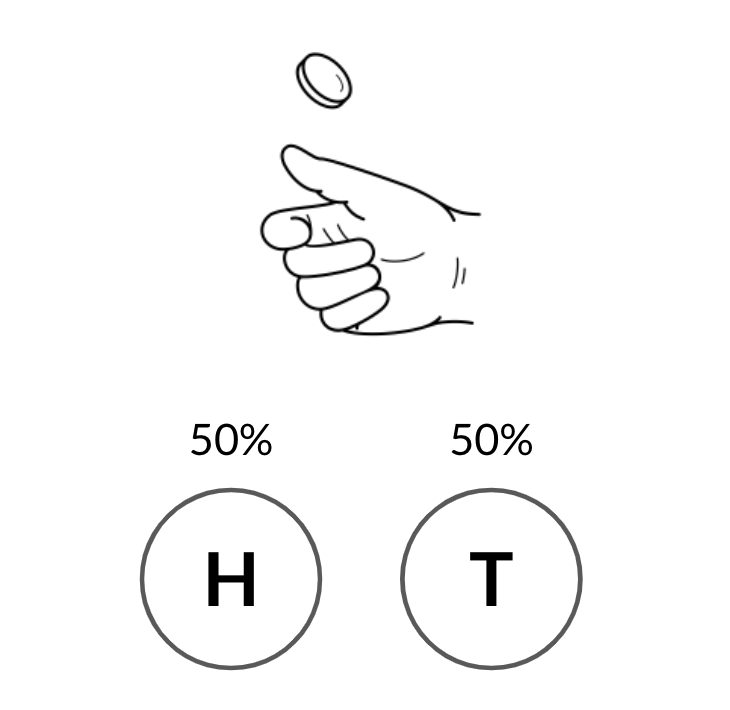
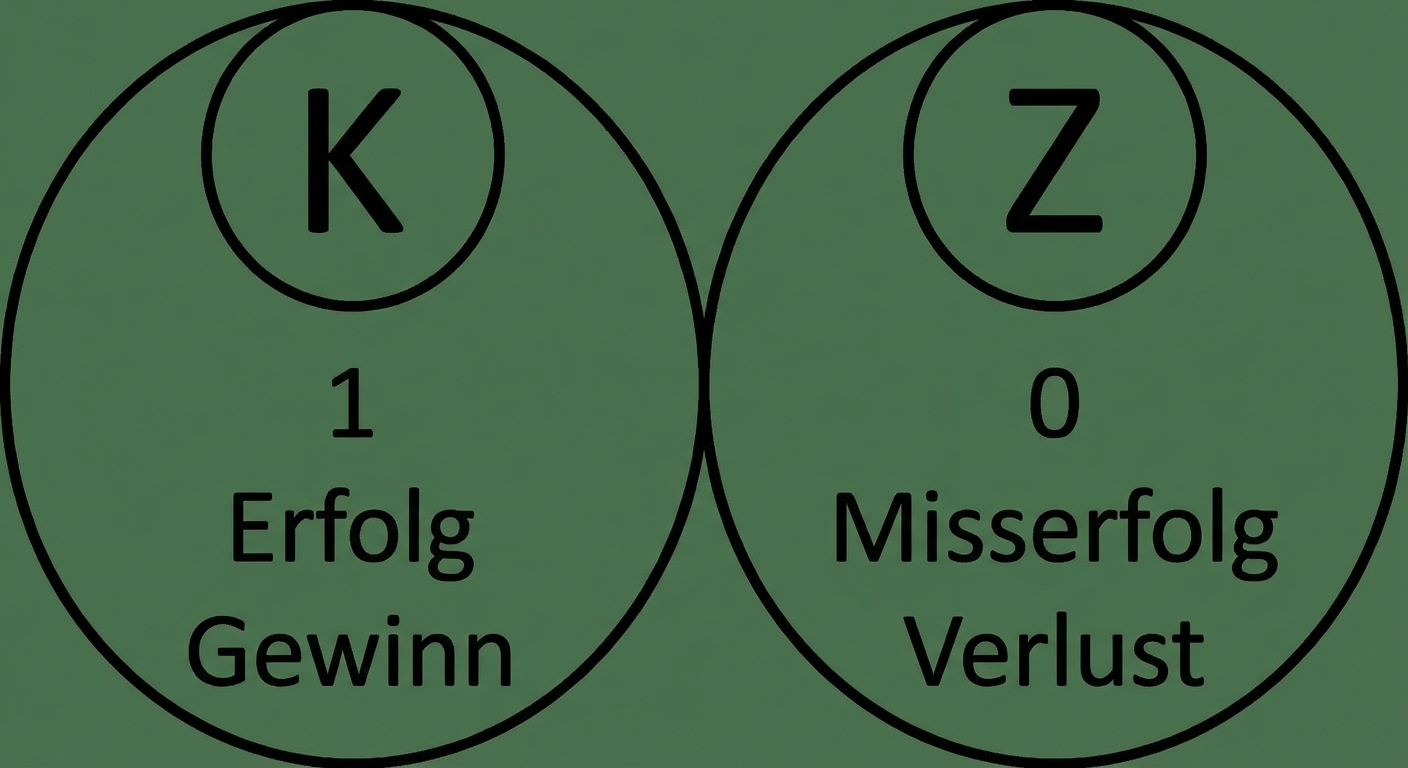
Binäre Ergebnisse
Viele Münzwürfe
| Münzwurf | Ergebnis |
|---|---|
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 0 |
| 6 | 0 |
| 7 | 1 |
| 8 | 0 |
| 9 | 1 |
| 10 | 1 |
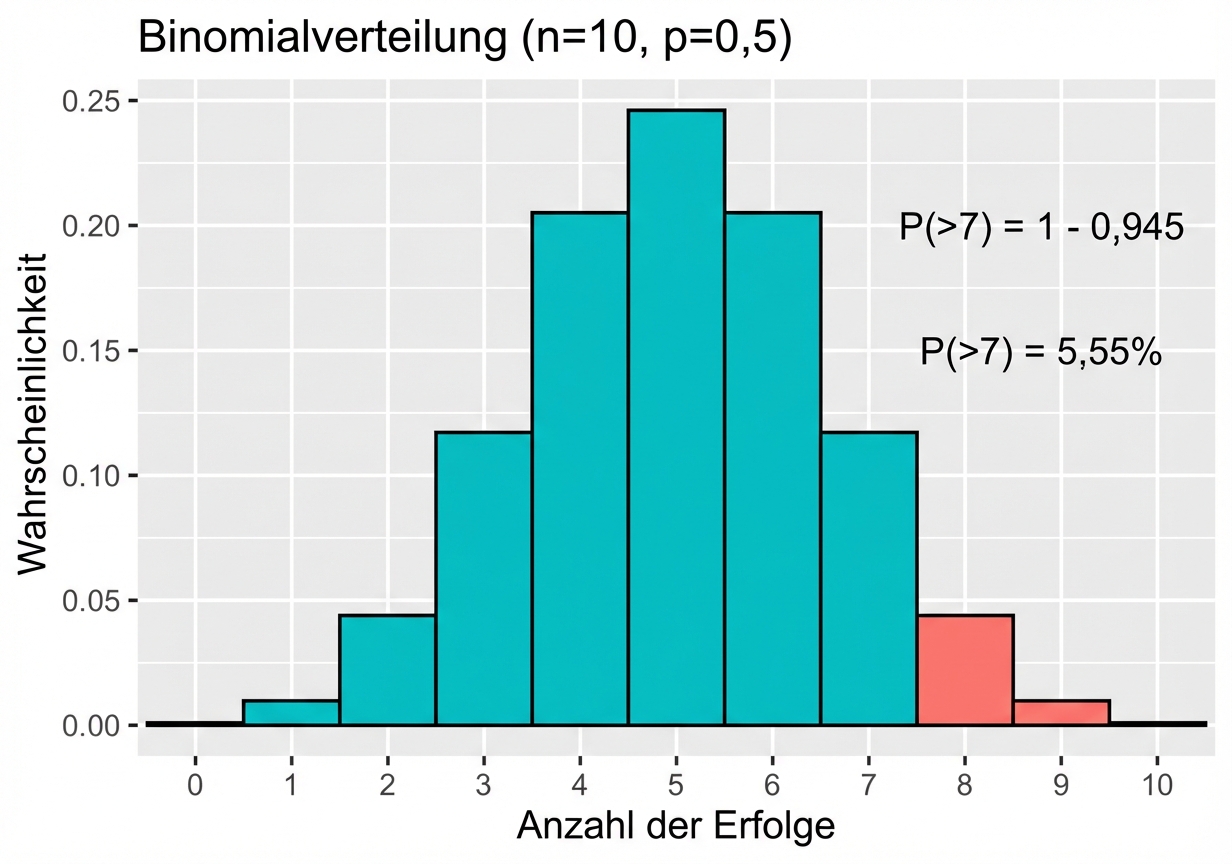
Binomialverteilung
Wahrscheinlichkeitsverteilung der Anzahl von Erfolgen in einer Folge von unabhängigen Ereignissen
Zum Beispiel die Anzahl der Kopfseiten in einer Folge von Münzwürfen
Beschrieben durch $n$ und $p$
- $n$: Gesamtzahl der Ereignisse
- $p$: Erfolgswahrscheinlichkeit
Binomialverteilung
Wahrscheinlichkeit für sieben oder weniger Mal Kopfseite
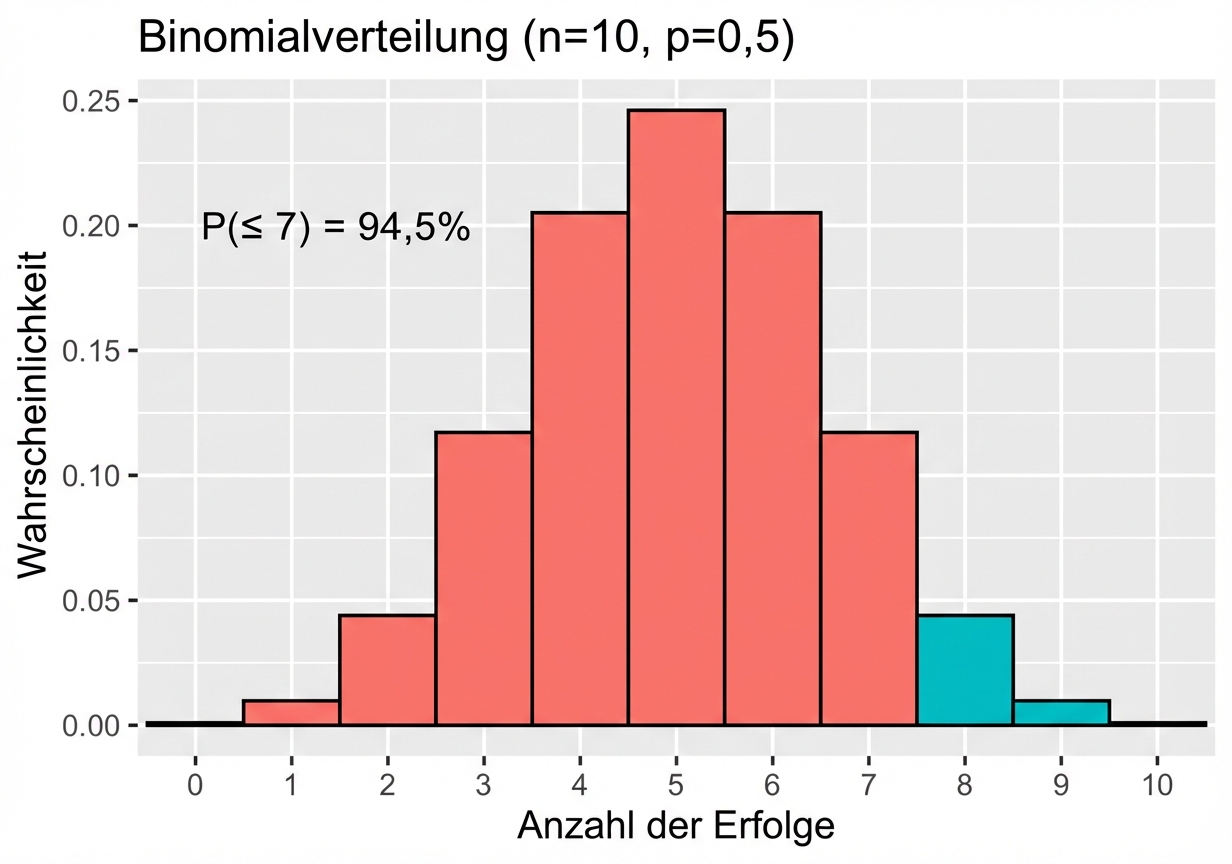
Wahrscheinlichkeit für acht Mal oder öfter Kopfseite
Erwartungswert
${Erwartungswert} = n \times p$
Erwartete Anzahl für die Kopfseite aus zehn Würfen $= 10 \times 0,5 = 5$
Wenn wir $p$ nicht kennen, jedoch $n$ und den Erwartungswert kennen:
${p} = \frac{Erwartungswert}{n} $
Unabhängigkeit
Die Binomialverteilung ist eine Verteilung für die Anzahl der Erfolge einer Reihe unabhängiger Ereignisse
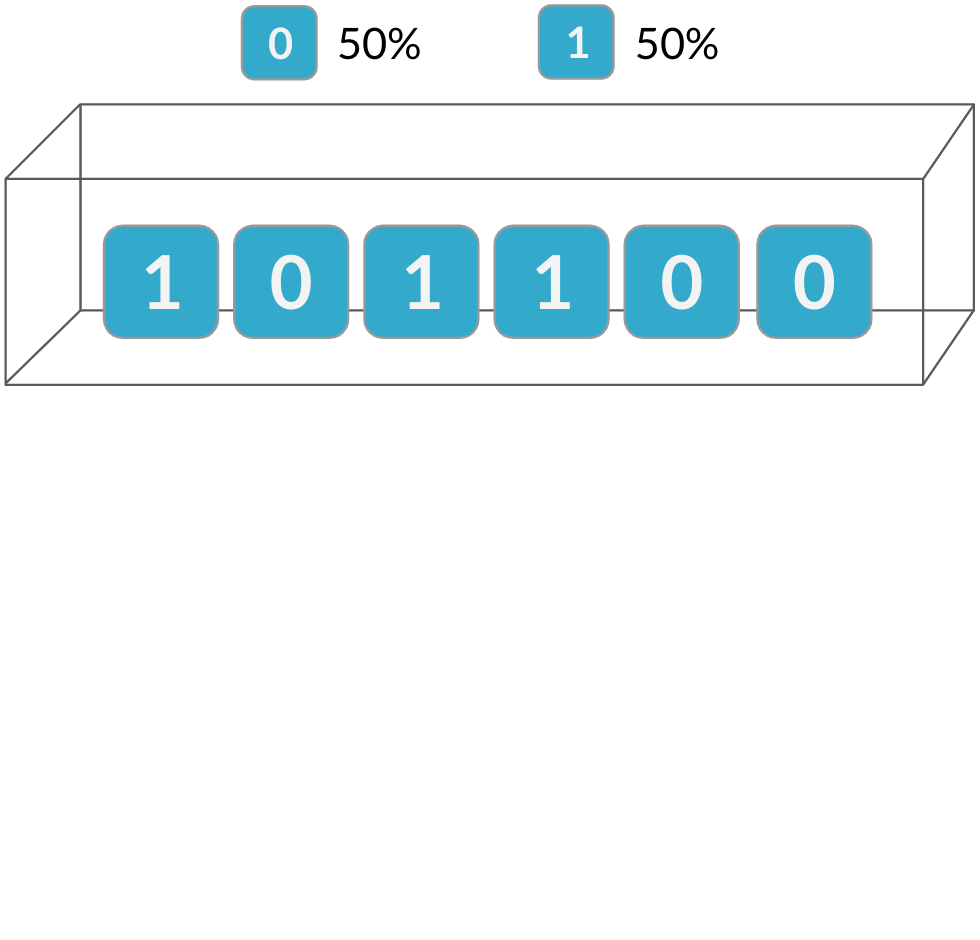
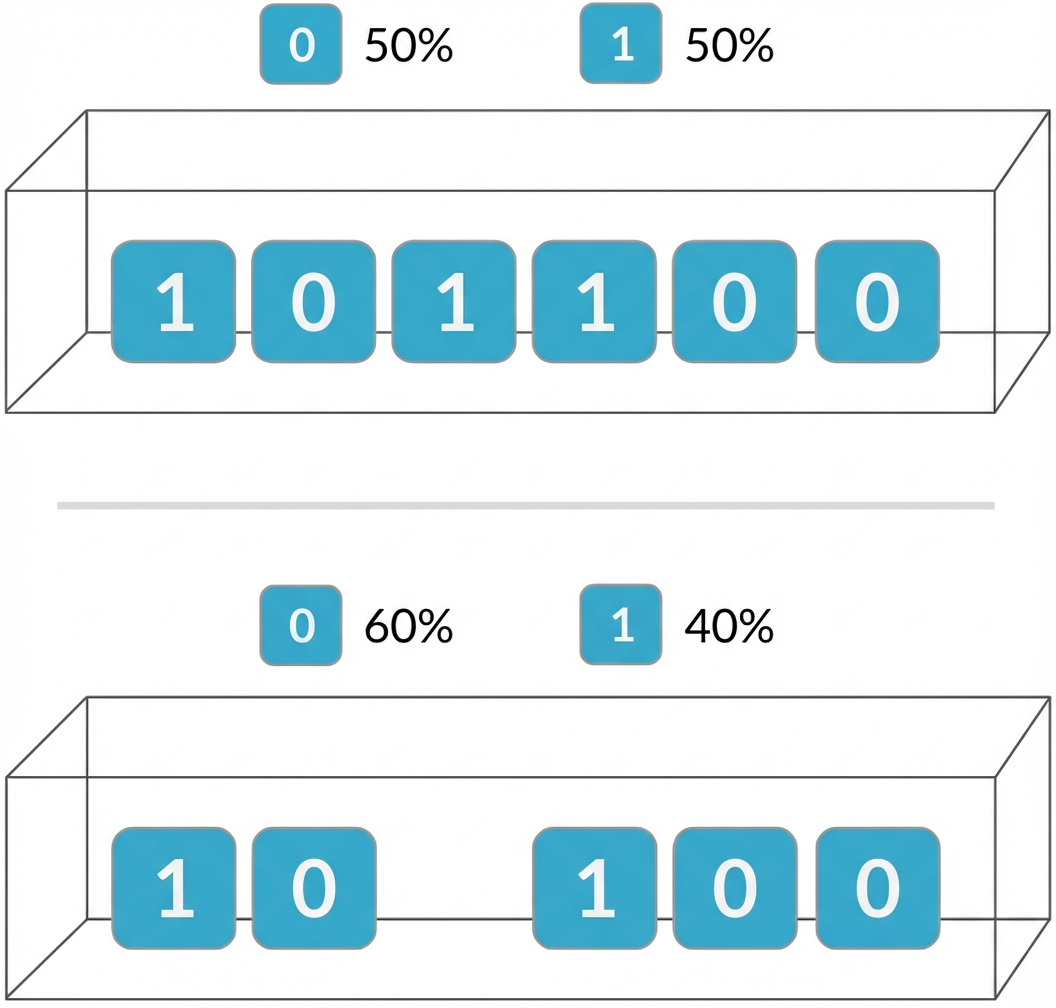
Unabhängigkeit
Die Binomialverteilung ist eine Verteilung für die Anzahl der Erfolge einer Reihe unabhängiger Ereignisse
Die Wahrscheinlichkeiten der nachfolgenden Ereignisse ändern sich abhängig vom ersten Ergebnis
Wenn die Ereignisse nicht unabhängig sind, gilt die Binomialverteilung nicht!
Allgemeine Anwendungen
Die Binomialverteilung kann für unabhängige Ereignisse mit binären Ergebnissen verwendet werden
- Klinische Studie zur Messung der Wirksamkeit von Medikamenten
- Effektiv oder nicht
- Sportwetten
- Wettende können gewinnen oder verlieren

Lass uns üben!
Einführung in die Statistik

