Kontinuierliche Verteilungen
Einführung in die Statistik

George Boorman
Curriculum Manager, DataCamp
Warten auf den Bus
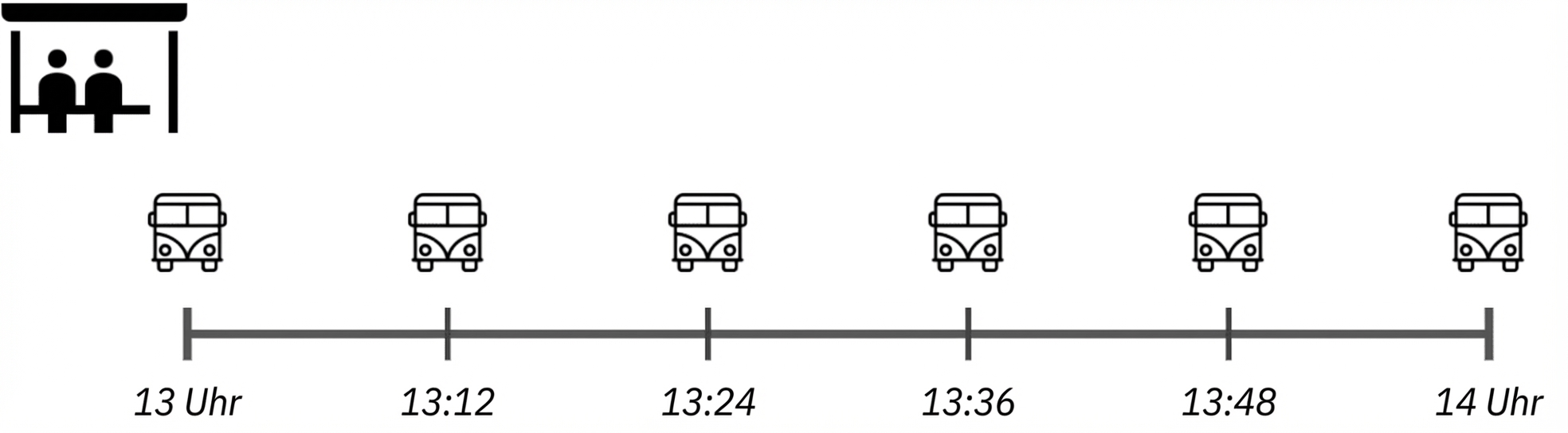
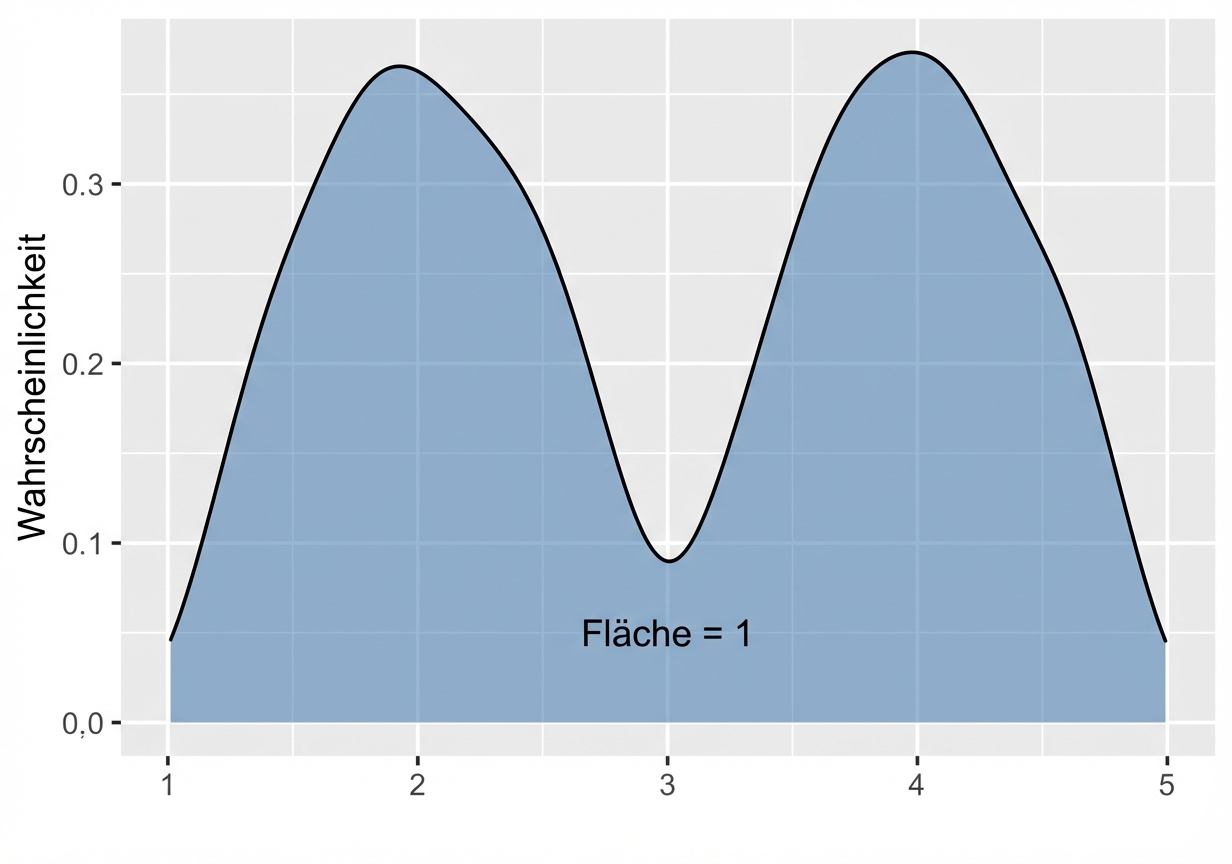
Stetige Gleichverteilung
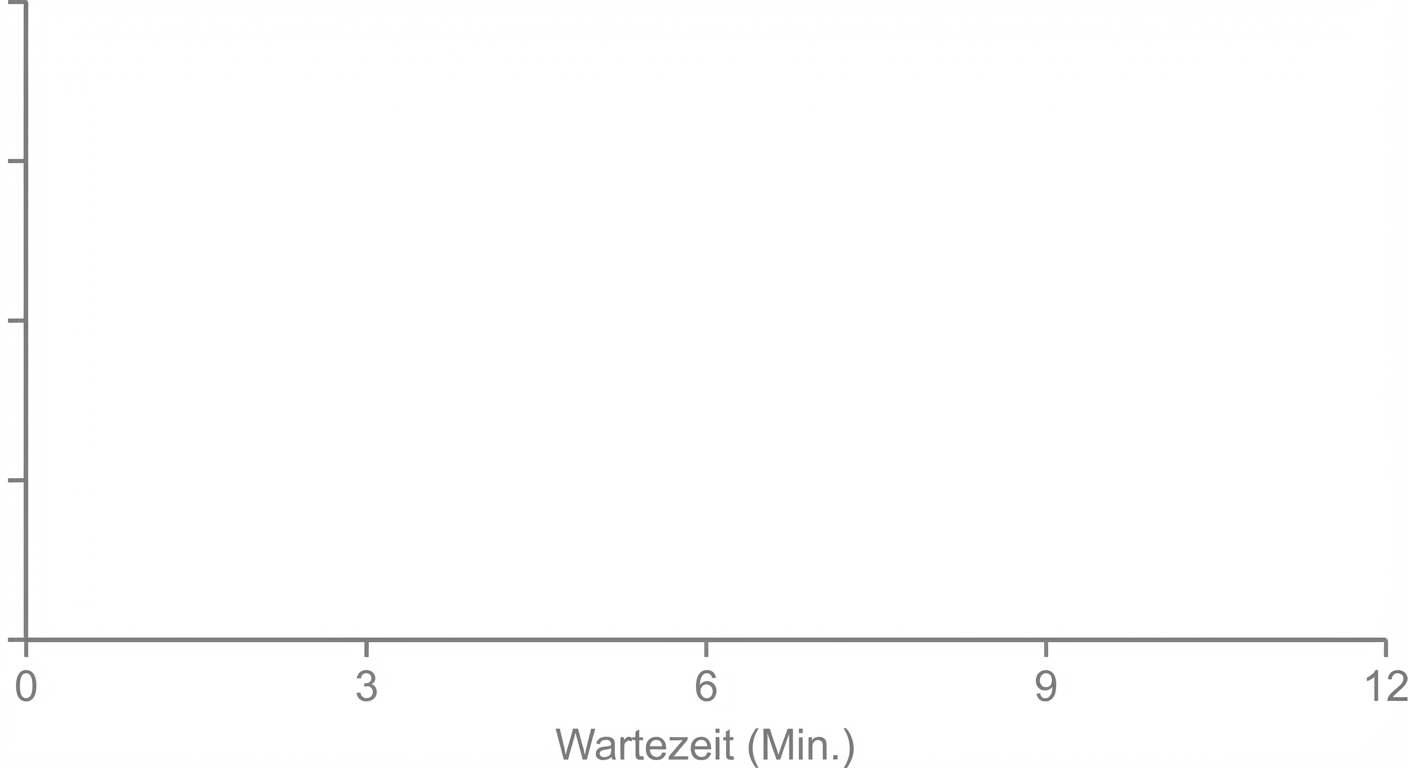
Stetige Gleichverteilung
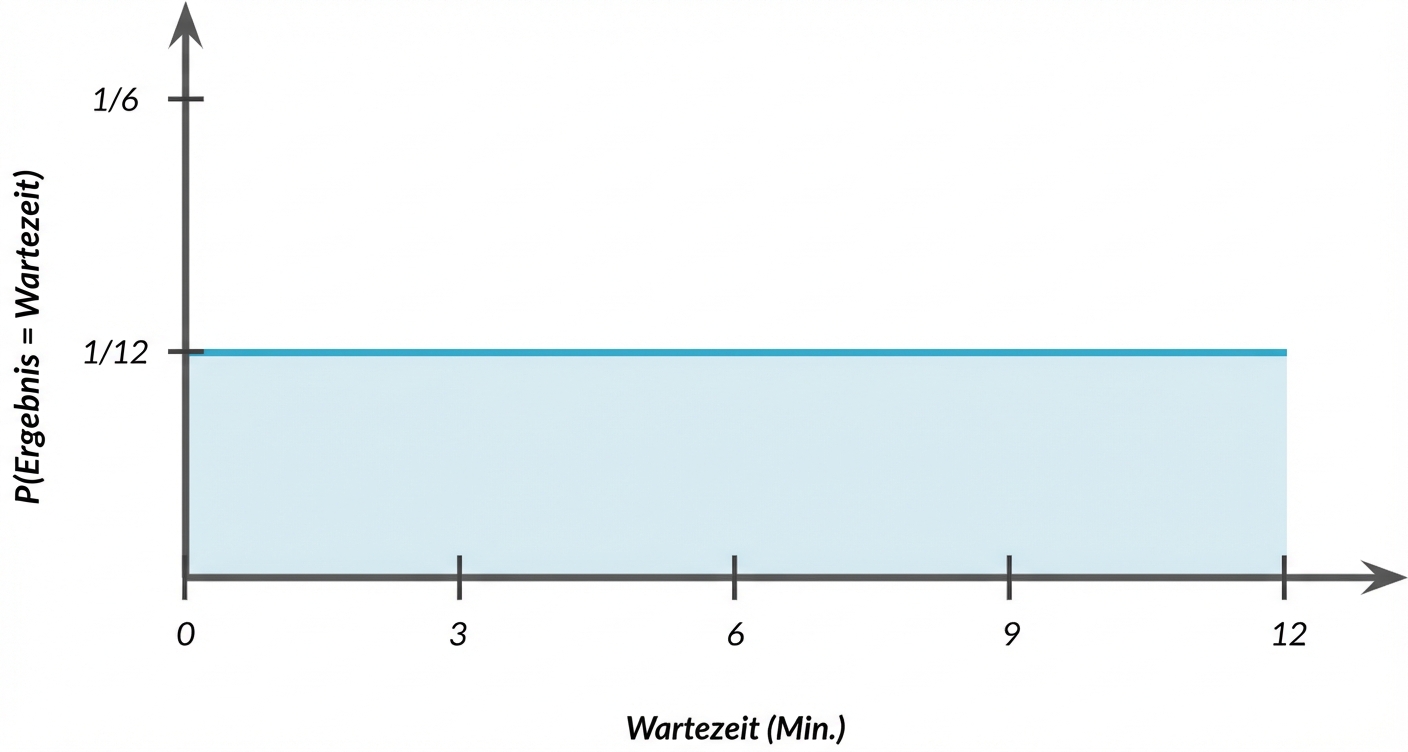
Erneut Wahrscheinlichkeit = Fläche
$$P(4 \le \text{Wartezeit} \le 7) = ~~ ?$$
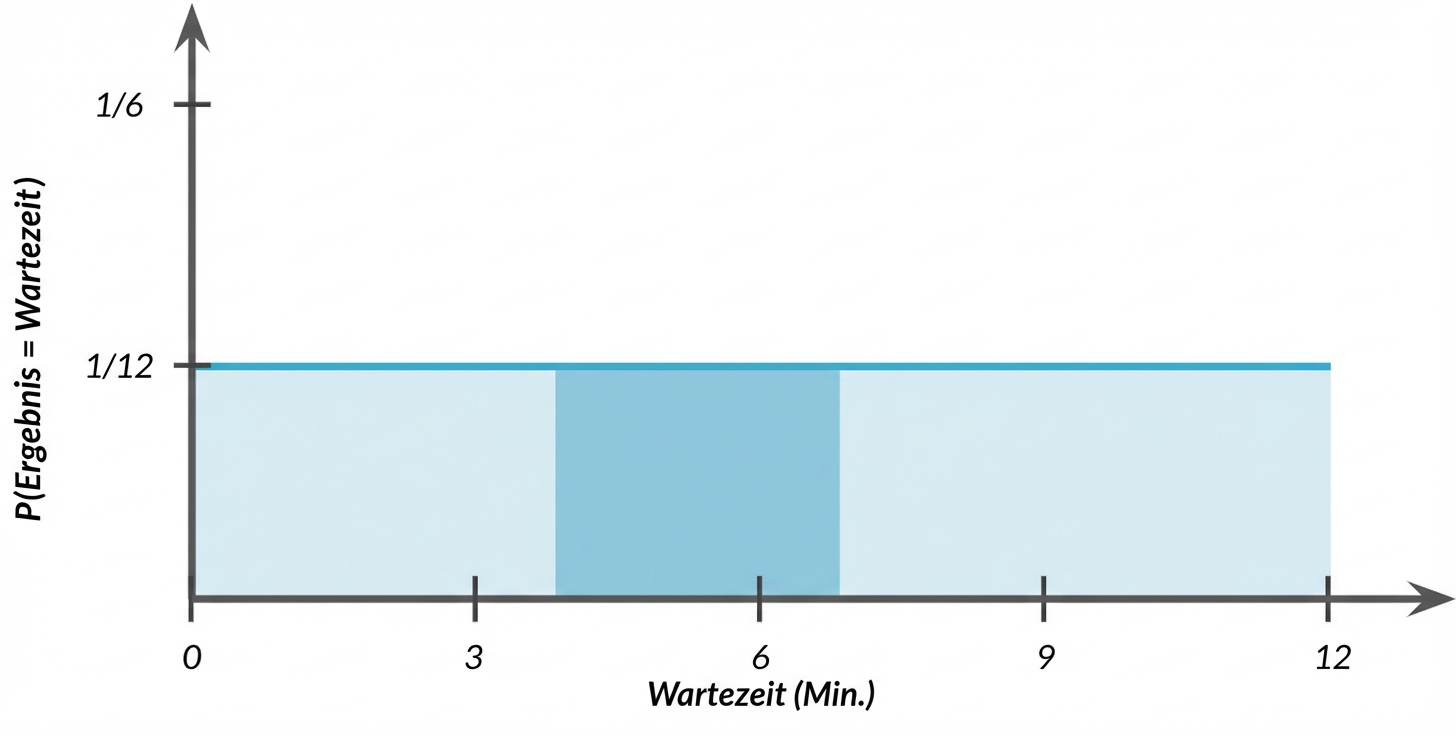
Erneut Wahrscheinlichkeit = Fläche
$$P(4 \le \text{Wartezeit} \le 7) = ~~ ?$$
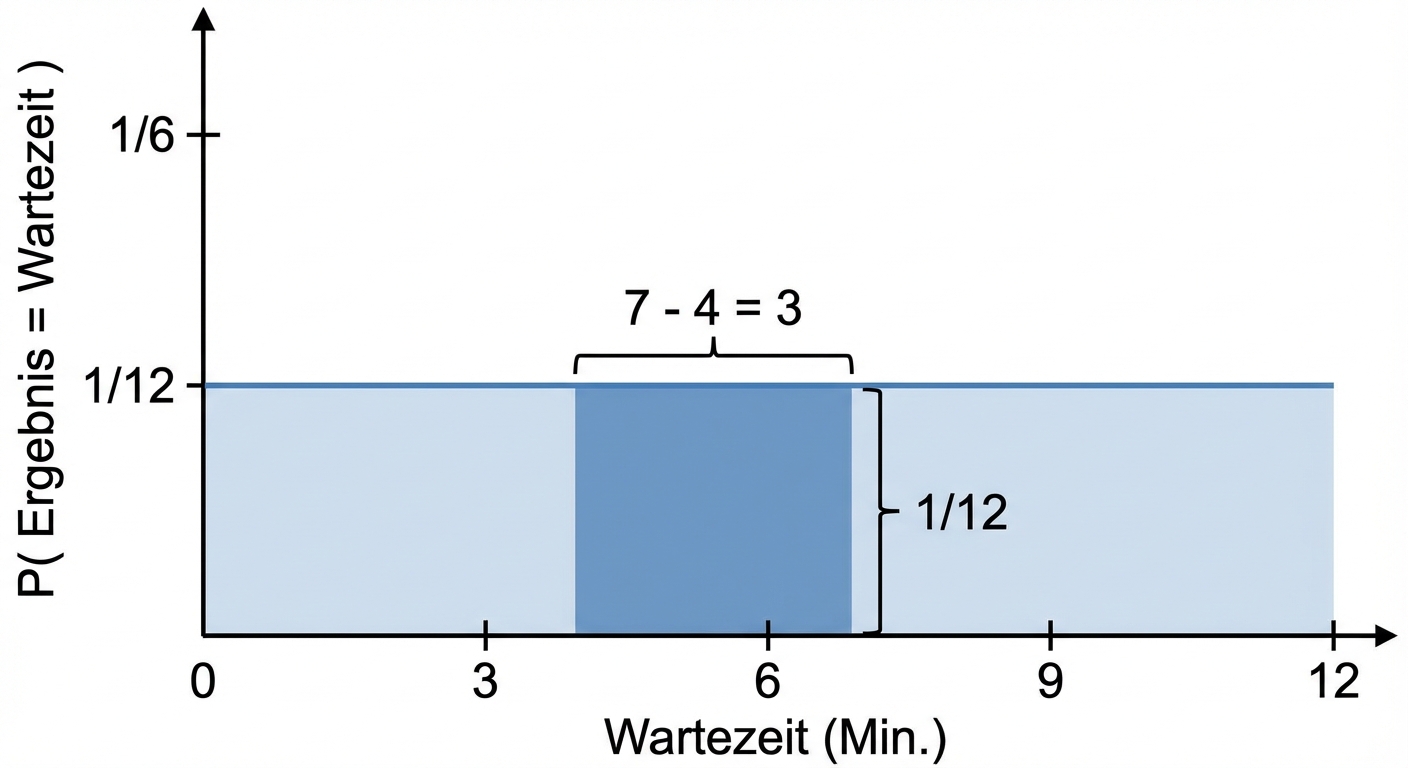
Erneut Wahrscheinlichkeit = Fläche
$$P(4 \le \text{Wartezeit} \le 7) = 3 \times 1/12 = 3/12$$

Sieben oder weniger Minuten Wartezeit
$$ P(\text{Wartezeit} \le 7) = ~~ ?$$
$$ P(\text{Wartezeit} \le 7) = \frac{7-0}{12} $$
$$ P(\text{Wartezeit} \le 7) = \frac{7}{12} = 58,33 \% $$
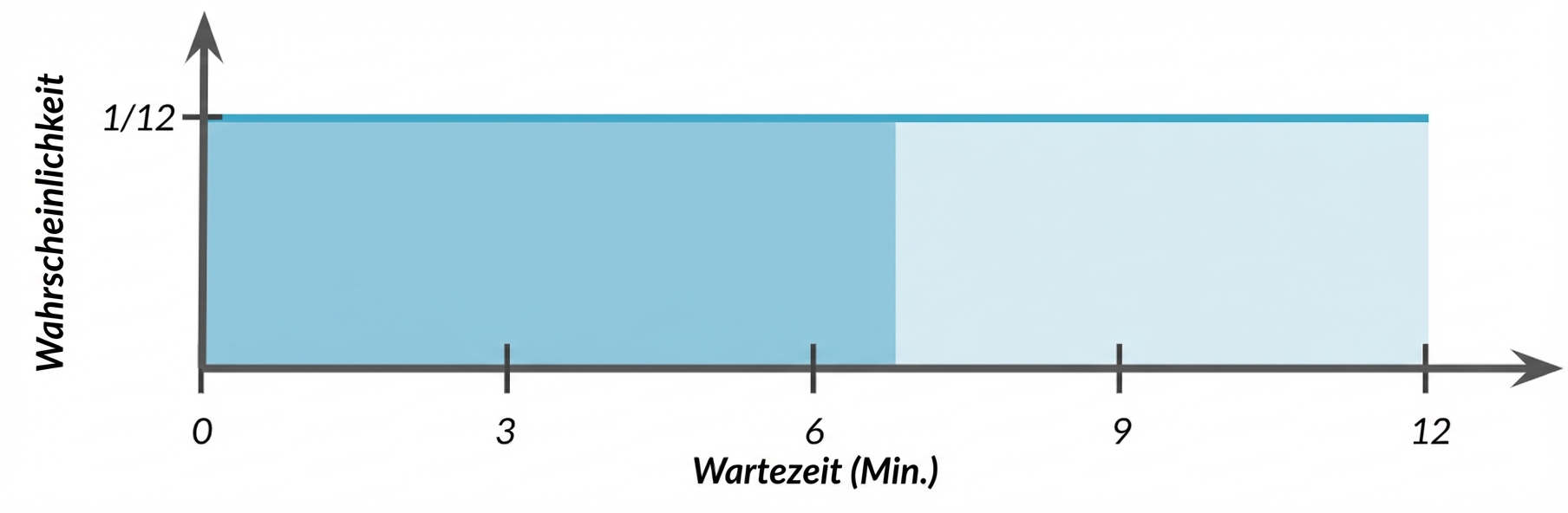
Gesamtfläche = 1
$$P(0 \le \text{Wartezeit} \le 12) = ~~ ?$$
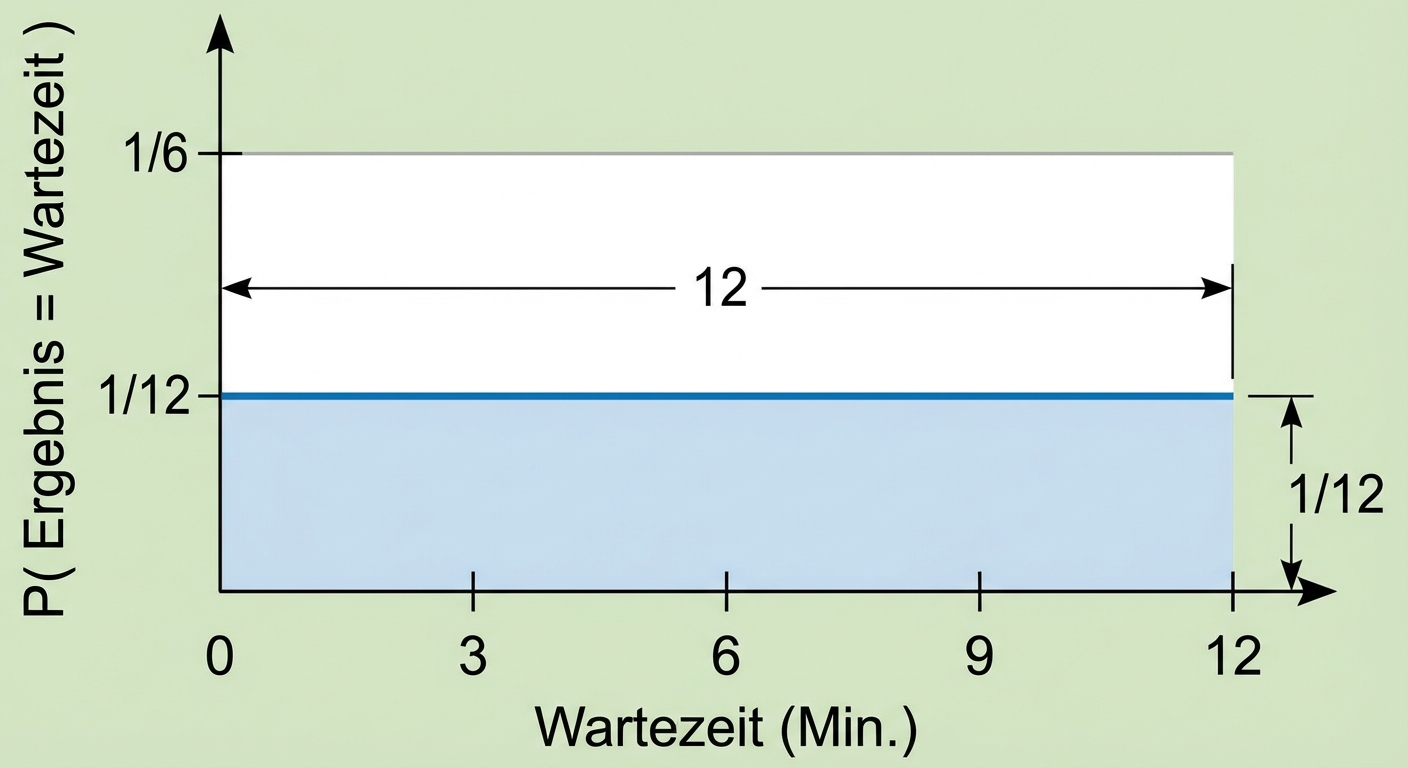
Gesamtfläche = 1
$$P(0 \le \text{Ergebnis} \le 12) = 12 \times 1/12 = 1$$
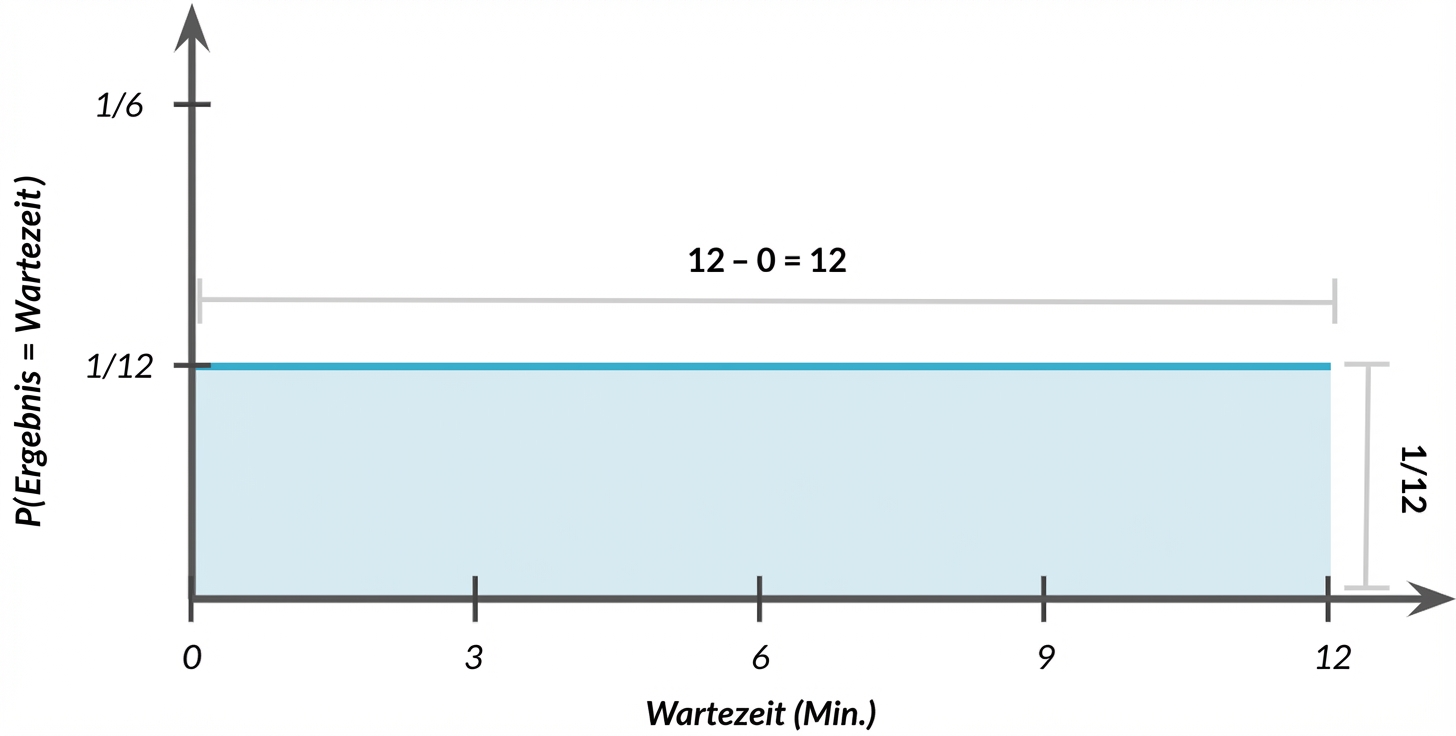
Die Wahrscheinlichkeit, mehr als sieben Minuten zu warten
$$ P(\text{Wartezeit} \ge 7) = 1 - \frac{7}{12} $$
$$ P(\text{Wartezeit} \ge 7) = \frac{5}{12} = 41,67 \% $$
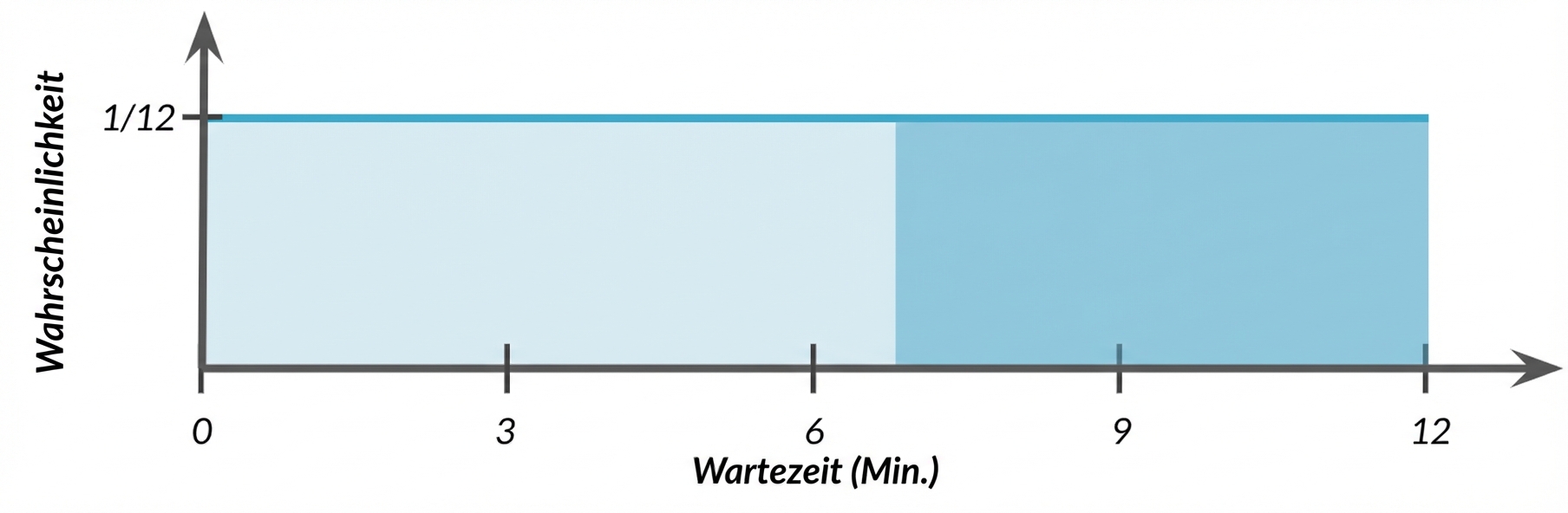
Bimodale Verteilung
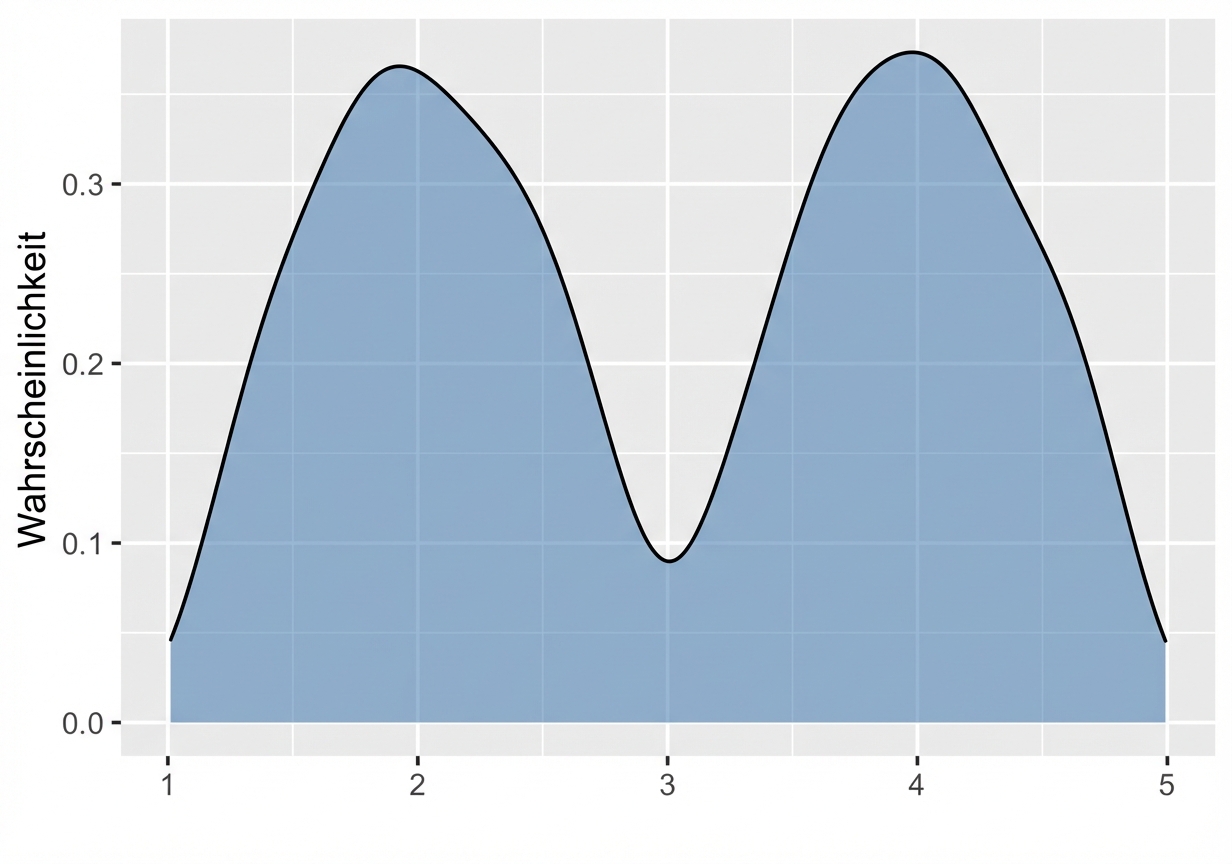
Die Normalverteilung
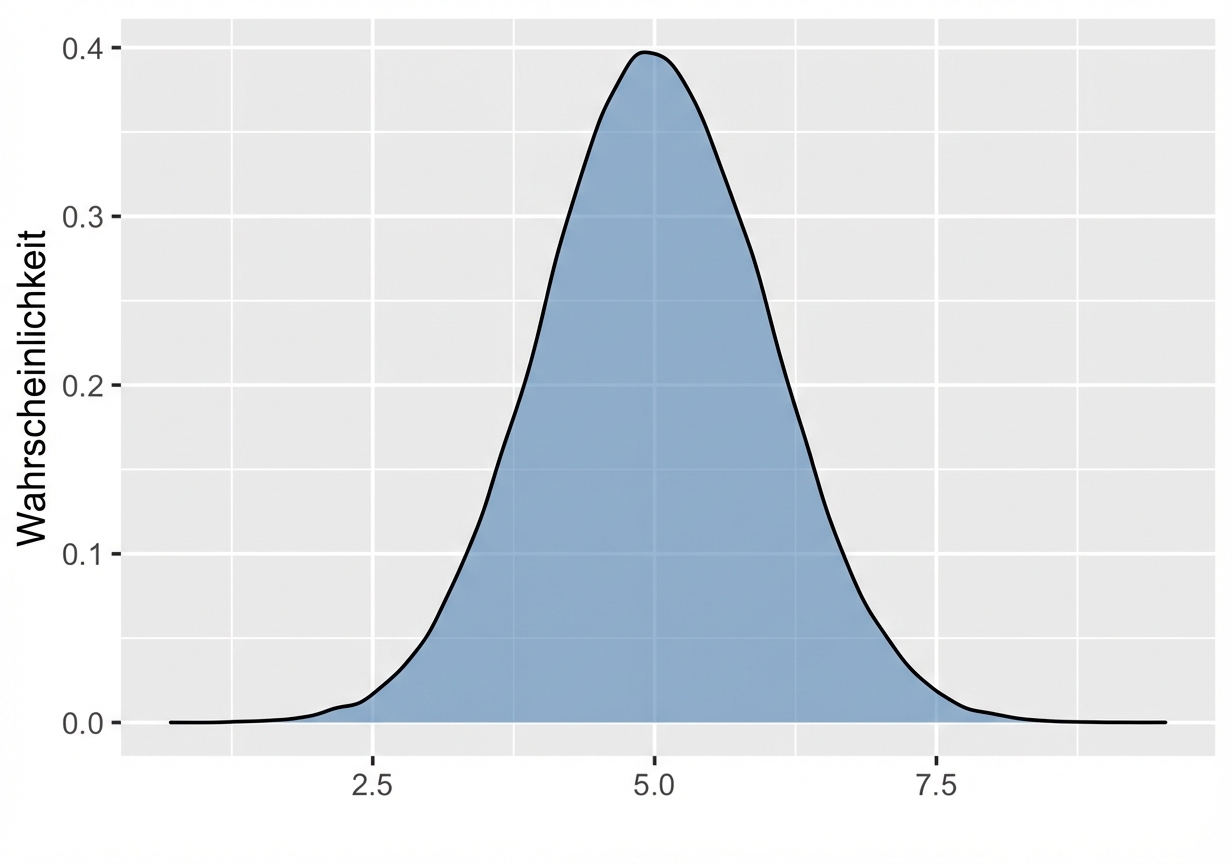
Erneut Gesamtfläche = 1
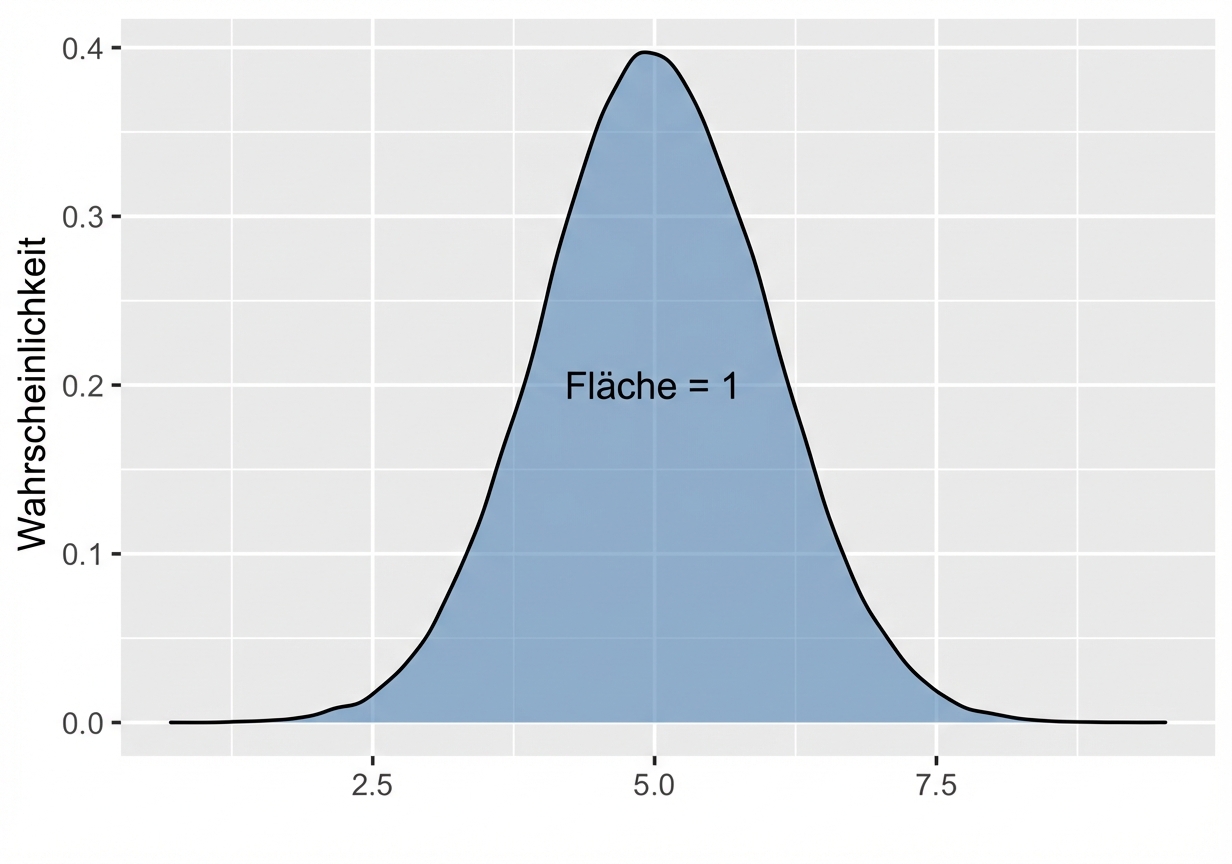
Lass uns üben!
Einführung in die Statistik

