Bedingte Wahrscheinlichkeit
Einführung in die Statistik

George Boorman
Curriculum Manager, DataCamp
Mehrere Meetings
Stichproben ohne Ersatz

Mehrere Meetings
Stichproben ohne Ersatz
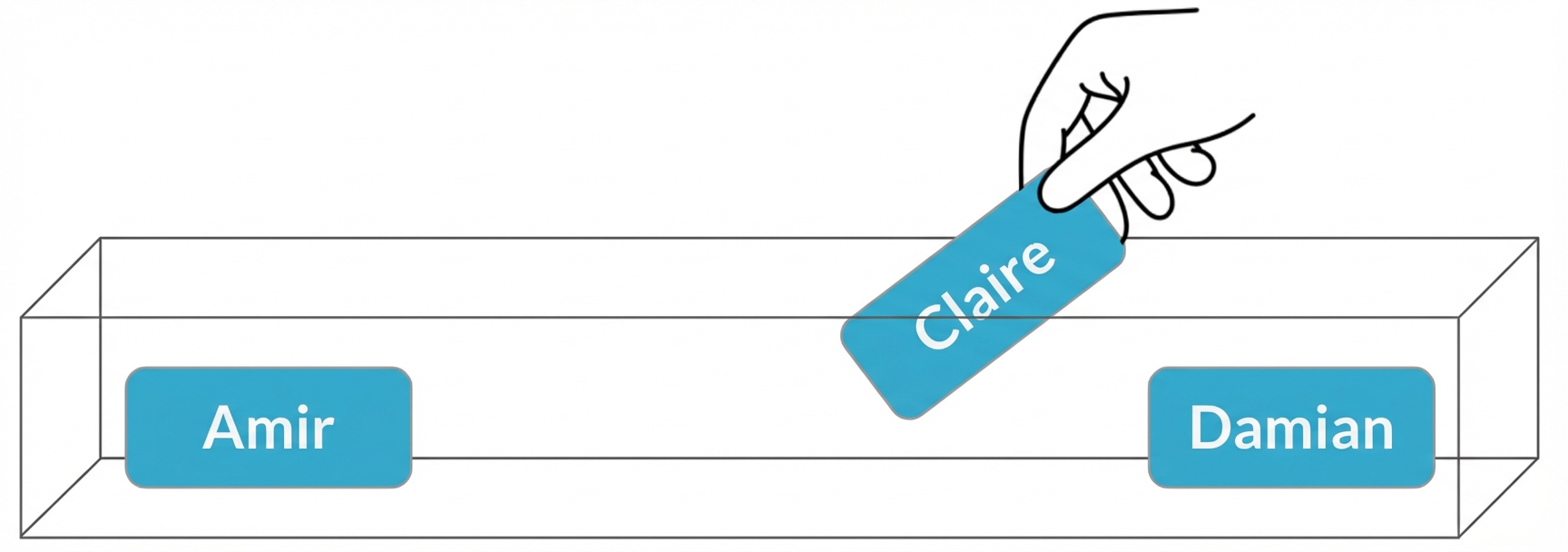
$$P(\text{Claire}) = \frac{1}{3} = 33\%$$
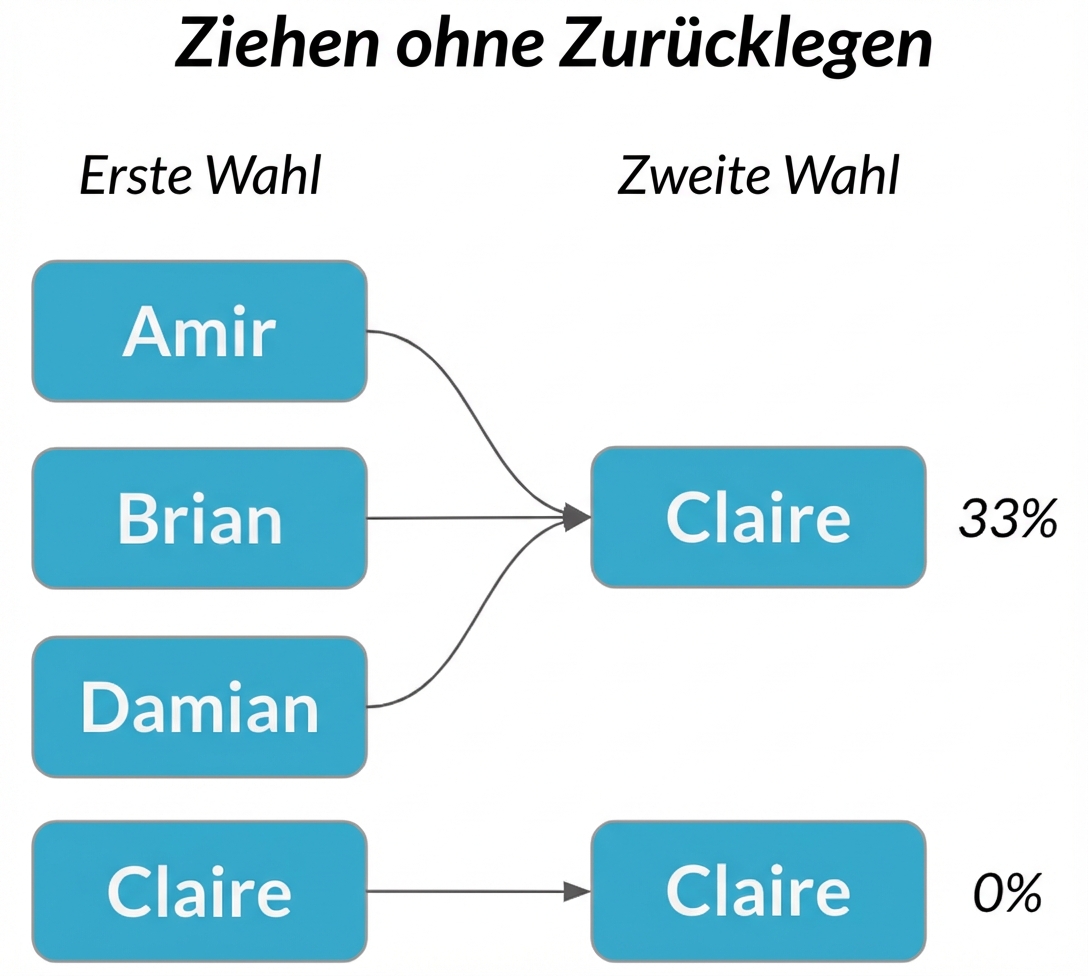
Abhängige Ereignisse
Die Wahrscheinlichkeit des zweiten Ereignisses wird durch den Ausgang des ersten Ereignisses beeinflusst

Abhängige Ereignisse
Die Wahrscheinlichkeit des zweiten Ereignisses wird durch den Ausgang des ersten Ereignisses beeinflusst
Abhängige Ereignisse
Die Wahrscheinlichkeit des zweiten Ereignisses wird durch den Ausgang des ersten Ereignisses beeinflusst
Stichprobe ohne Ersatz = jede Auswahl ist abhängig
Bedingte Wahrscheinlichkeit
Die bedingte Wahrscheinlichkeit wird verwendet, um die Wahrscheinlichkeit von abhängigen Ereignissen zu berechnen
- Die Wahrscheinlichkeit eines Ereignisses hängt vom Ergebnis eines anderen Ereignisses ab

Venn-Diagramme
Küchenverkäufe über 150 €
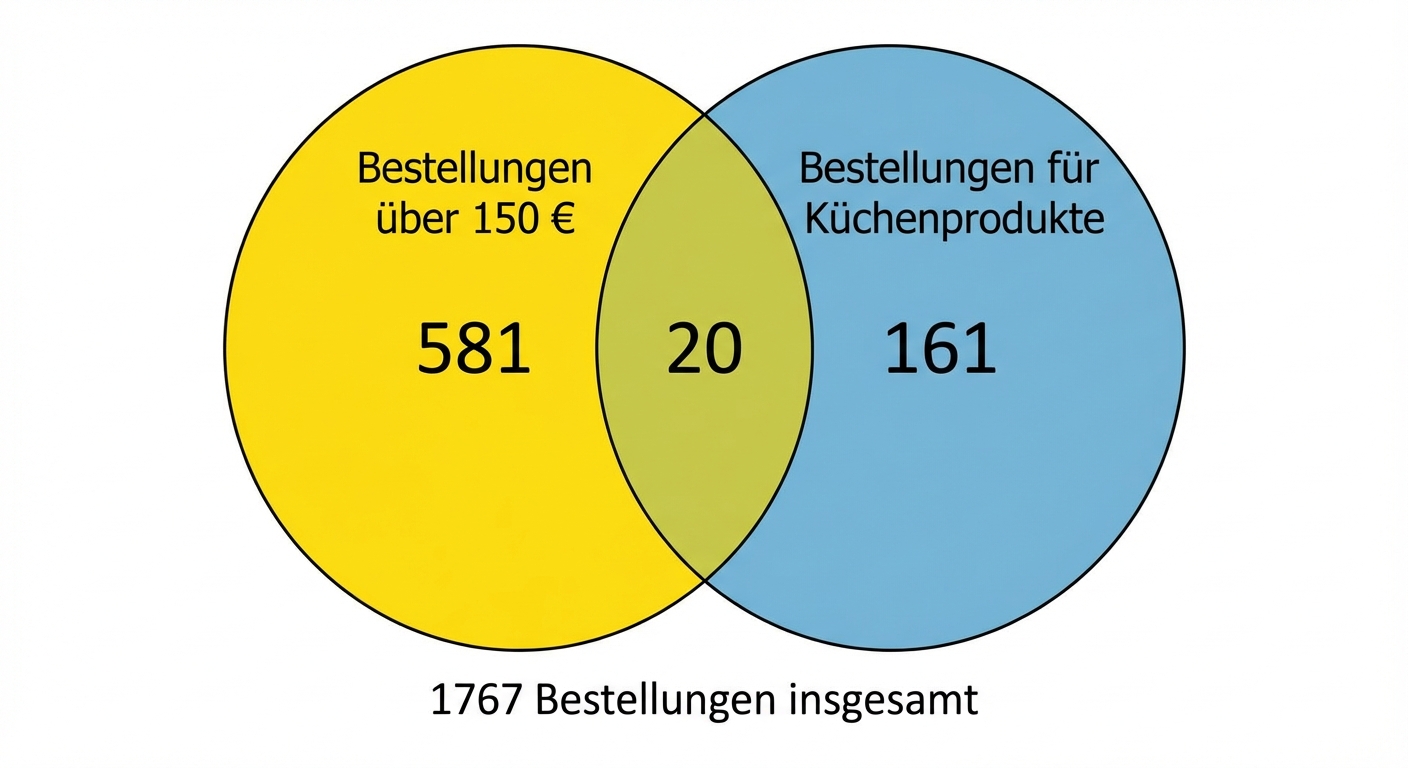
Küchenverkäufe über 150 €

$$P(Bestellung > 150 | Kueche) = \frac{\frac{20}{1767}}{\frac{181}{1767}}$$
$$P(Bestellung > 150 | Kueche) = \frac{20}{181} $$
Die Reihenfolge der Ereignisse ist wichtig
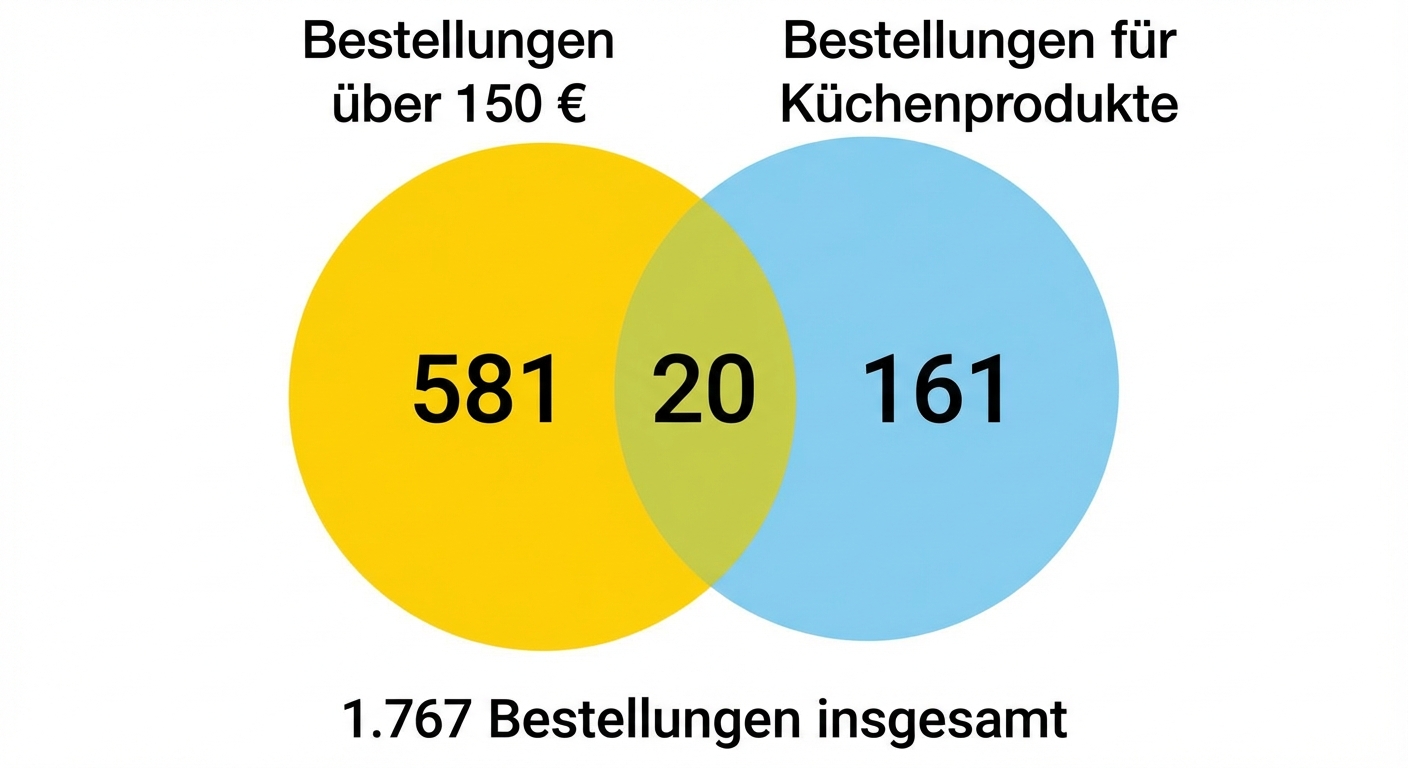
$$P(Kueche | Reihenfolge > 150) = \frac{\frac{20}{1767}}{\frac{601}{1767}}$$
$$P(Kueche | Bestellung > 150) = \frac{20}{601} $$
Formel für bedingte Wahrscheinlichkeit
$$P(A | B) = \frac{{P(A \ \cap \ B)}}{{P(B)}}$$
$P(A | B)$ → Wahrscheinlichkeit von Ereignis A , vorausgesetzt, Ereignis B tritt auf
$P(A \ \cap \ B)$ → Wahrscheinlichkeit von Ereignis A und Ereignis B
- Dividiert durch die Wahrscheinlichkeit des Ereignisses B → $P(B)$
Lass uns üben!
Einführung in die Statistik

