Maße der Streuung

Einführung in die Statistik

George Boorman

Curriculum Manager, DataCamp

Was ist Streuung?

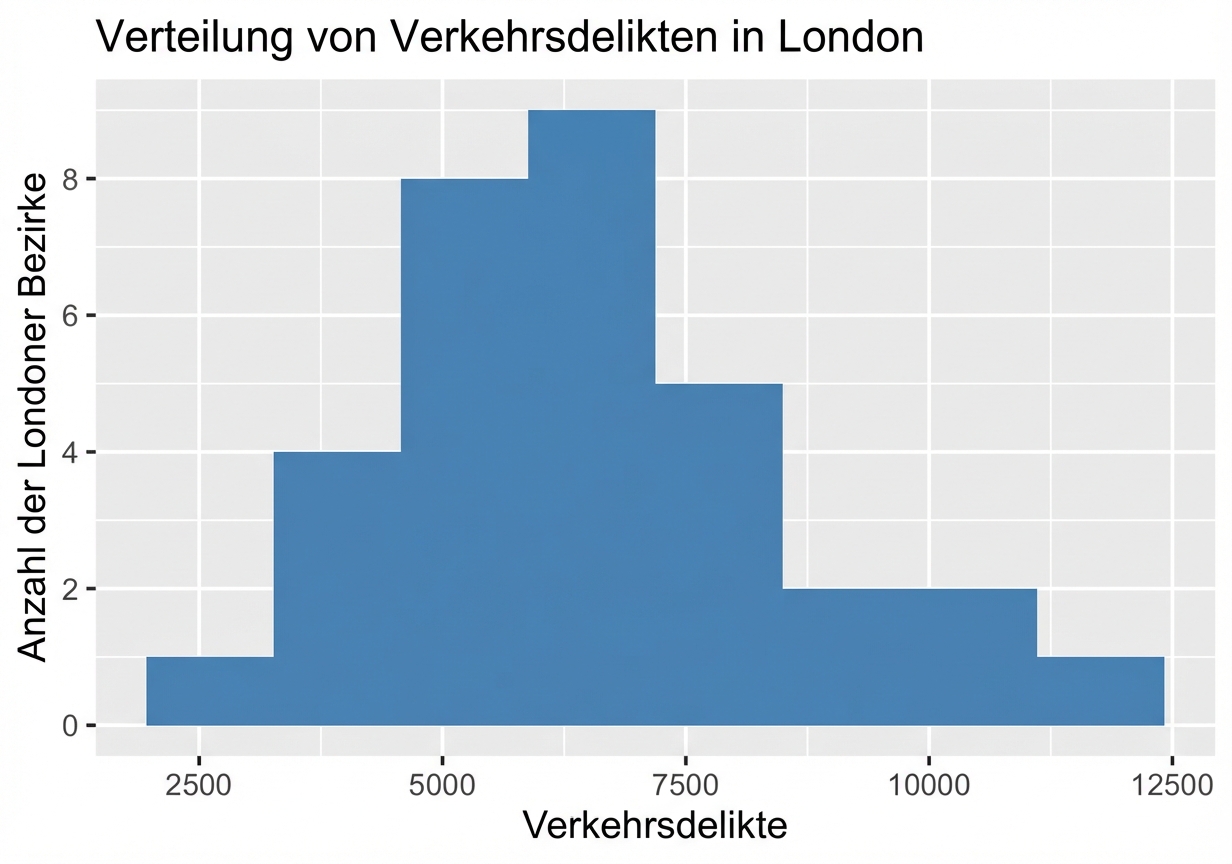
vehicle_crimes_histogram_with_wide_spread.png

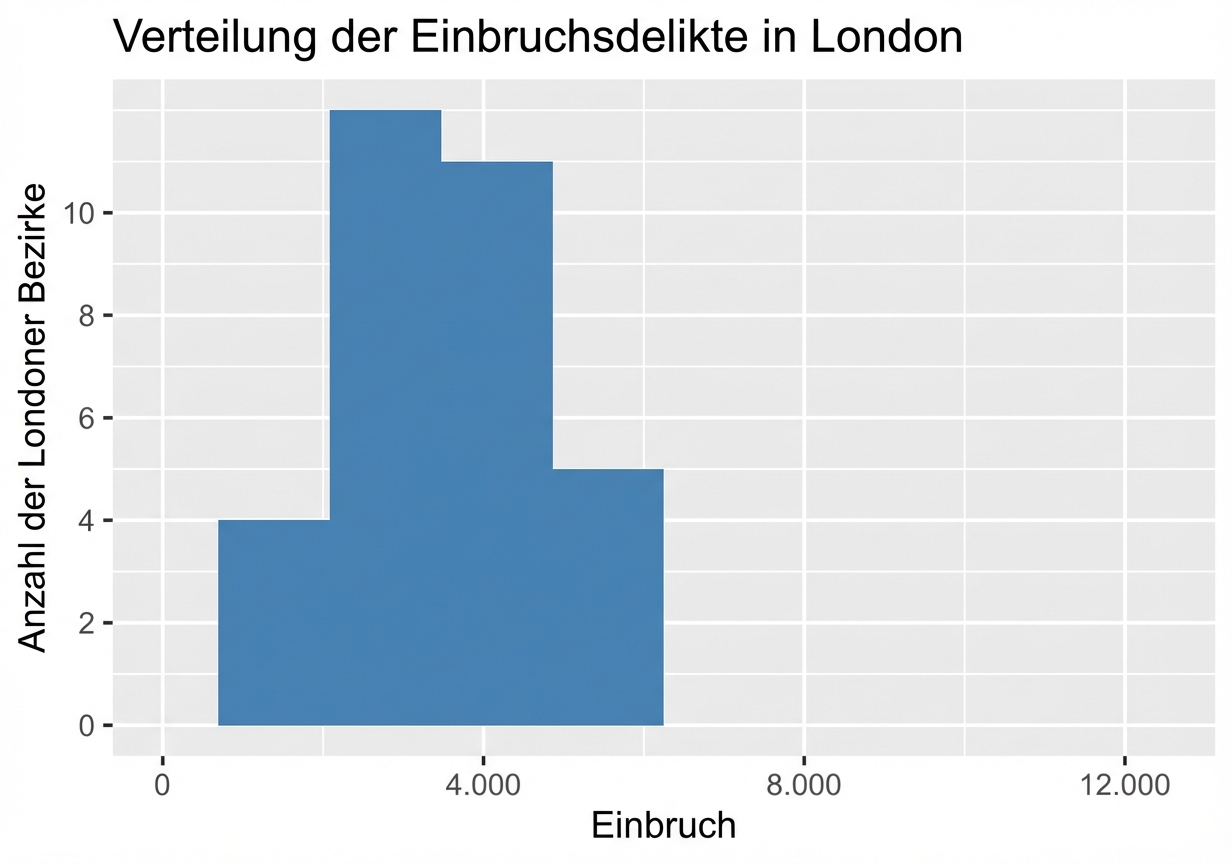
burlgary_crimes_histogram_with_narrow_spread.png

Einführung in die Statistik

Warum ist die Streuung wichtig?

  • Die Streuung misst die Vielfalt der Daten

 

  • T-Shirts kosten normalerweise 30 €

    • Können zwischen 10-200 € kosten
    • Wie wahrscheinlich ist es, dass eines 30 € kostet?

  • Wenn T-Shirts zwischen 20-50 € kosten würden

    • Ändert das etwas an der Wahrscheinlichkeit, eines für 30 € zu finden?

t_shirt_hanging_against_a_wall.jpg

1 Bildnachweis: https://unsplash.com/@uyk
Einführung in die Statistik

Spannweite

 

${Spannweite} = Maximum - Minimum$

 

${Spannweite(Einbrueche)} = 5.183 - 1.432$

${Spannweite(Einbrueche)} = 3.751$

Stadtbezirk Einbruch
Tower Hamlets 5.183
Hackney 5.079
Barnet 5.067
... ...
Sutton 1.815
Bexley 1.583
Kingston upon Thames 1.432
Einführung in die Statistik

Varianz

Ein Punktdiagramm mit einer roten Linie in der Mitte, die den Mittelwert darstellt.png

Einführung in die Statistik

Varianz

variance_plot_showing_distance_between_Westminster_and_the_mean.png

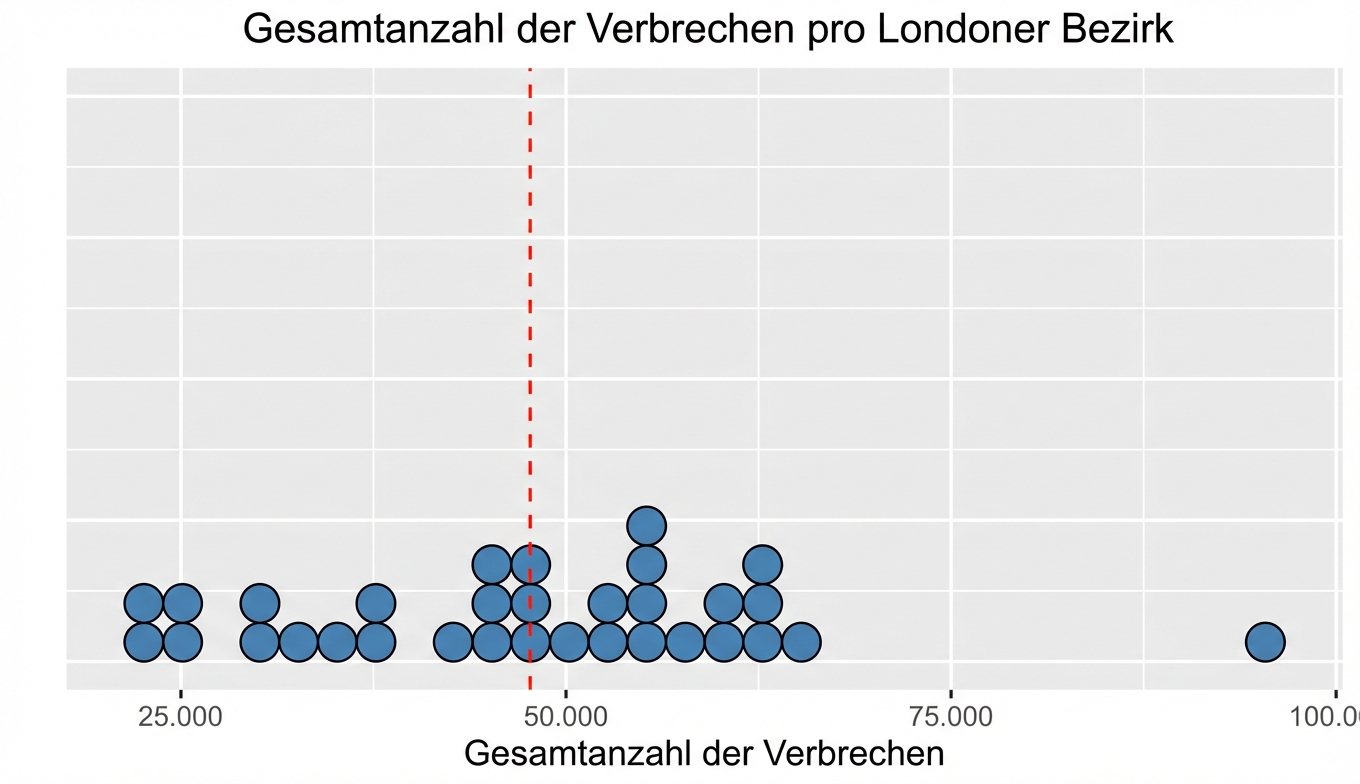
Einführung in die Statistik

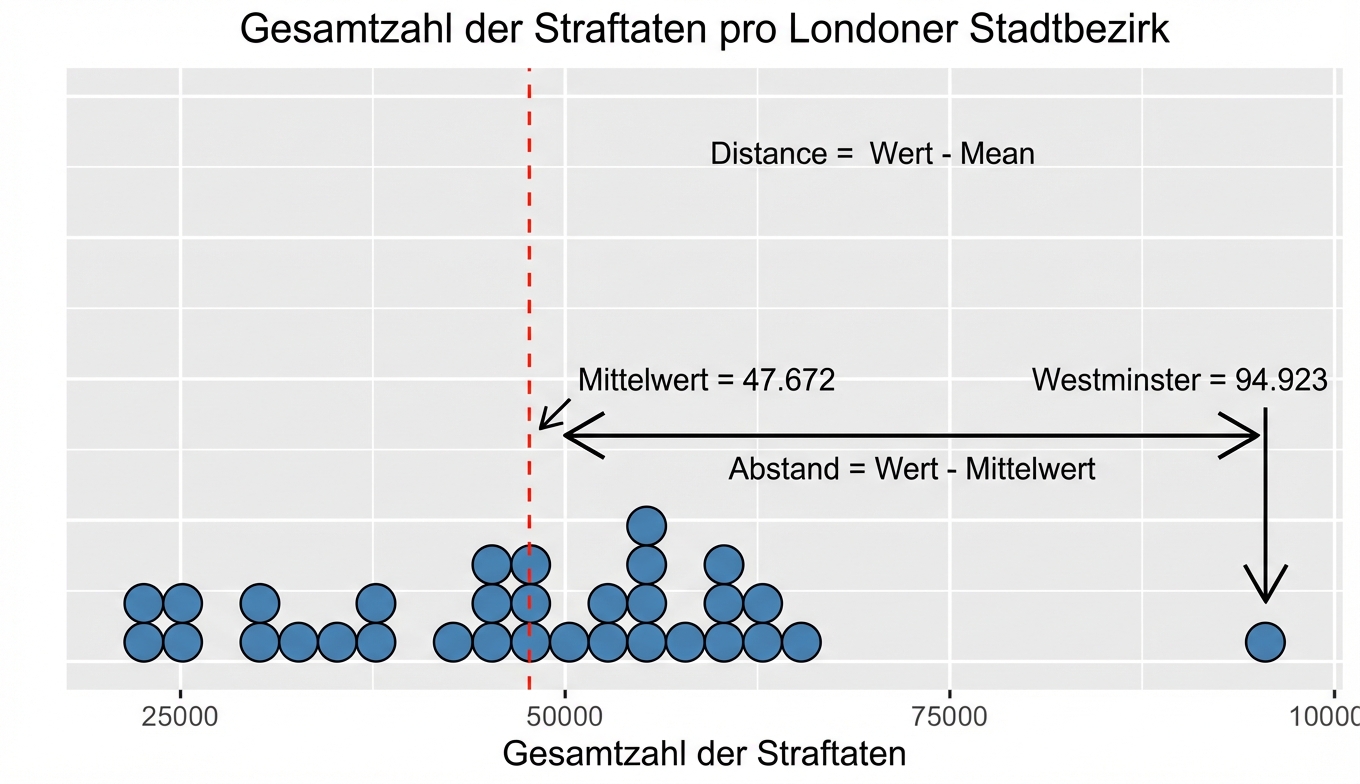
Varianz

Stadtbezirk Gesamtkriminalität Mittelwert Distanz
Barking und Dagenham 37.939 47.672 -9.733
Barnet 52.421 47.672 4.749
Bexley 29.285 47.672 -18.387
Brent 55.465 47.672 7.793
Bromley 42.982 47.672 -4.690
Camden 54.806 47.672 7.134
... ... ... ...
Gesamt 1.525.492 1.525.492 0
Einführung in die Statistik

Varianz

Stadtbezirk Gesamtkriminalität Mittelwert Distanz Quadrierte Distanz
Barking und Dagenham 37.939 47.672 -9.733 94.731.289
Barnet 52.421 47.672 4.749 22.553.001
Bexley 29.285 47.672 -18.387 338.081.769
Brent 55.465 47.672 7.793 60.730.849
Bromley 42.982 47.672 -4.690 21.996.100
Camden 54.806 47.672 7.134 50.893.956
... ... ... ... ...
Gesamt 1.525.492 1.525.492 0 7.509.750.824
Einführung in die Statistik

Varianz

 

$${Varianz(Gesamtkriminalitaet)} = \frac{7.509.750.824}{32}$$

$${Varianz(Gesamtkriminalitaet)} = \ 234.679.713$$

Einführung in die Statistik

Standardabweichung

${Standardabweichung (Gesamtkriminalitaet)} = {\sqrt( Varianz(Gesamtkriminalitaet))}$

${Standardabweichung(Gesamtkriminalitaet)} = {\sqrt(234.679.713)}$

${Standardabweichung(Gesamtkriminalitaet)} = 15.319,26$

  • Standardabweichung nahe Null = Daten um den Mittelwert geclustert
Einführung in die Statistik

Standardabweichung in einem Histogramm

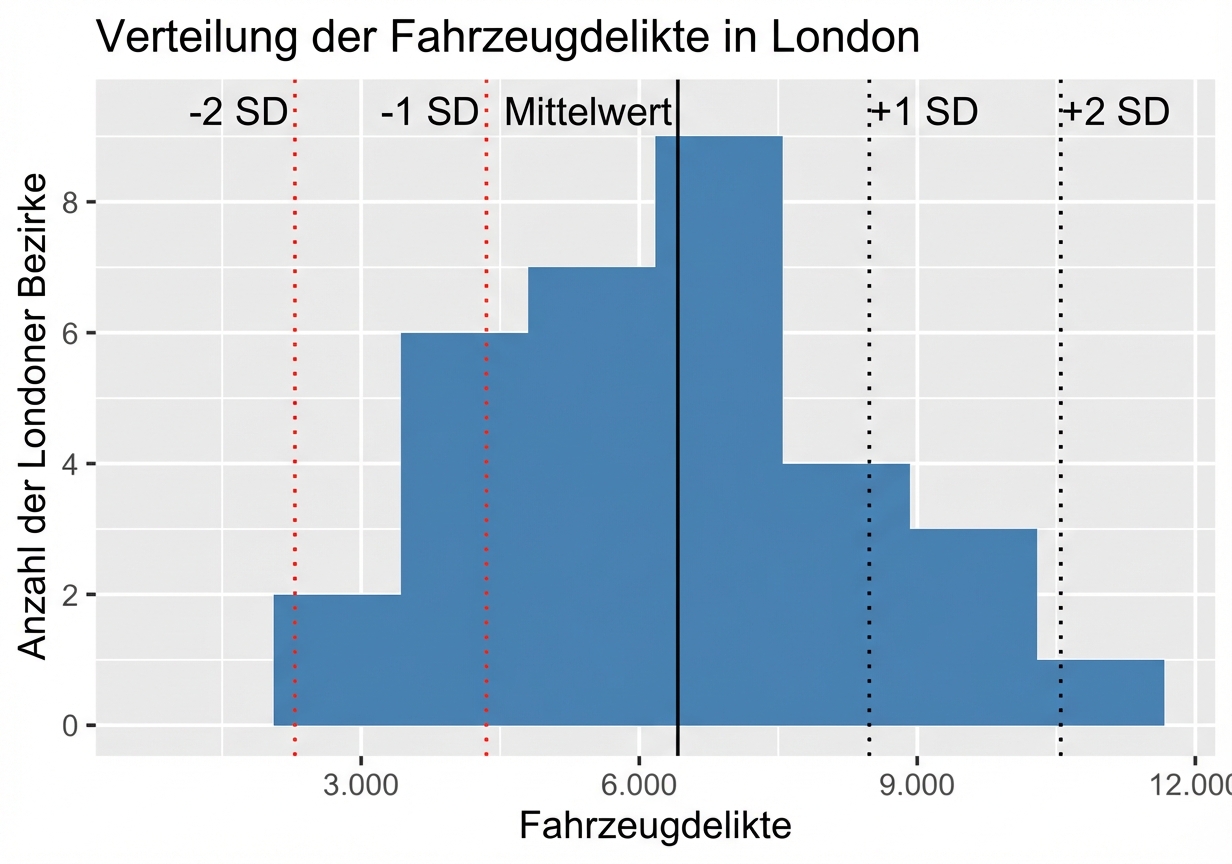
vehicle_crime_histogram_with_one_and_two_standard_deviations_from_the_mean.png

Einführung in die Statistik

Quartile

  • Quartile:
    • Aufteilung der Daten in vier gleiche Teile

 

Verbrechen 0 % 25 % 50 % 75 % 100 %
Einbruch 1.432,00 2.681,75 3.416,50 4.392,00 5.183,00
Raubüberfall 363,00 895,75 1.354,50 1.976,50 4.156,00
Diebstahl 4.090,00 7.739,75 9.624,00 12.059,00 40.278,00
Verkehrsdelikte 2.143,00 4.838,25 6.424,50 7.520,75 11.292,00
Einführung in die Statistik

Quartile

  • Quartile:
    • Aufteilung der Daten in vier gleiche Teile

 

Verbrechen 0 % 25 % 50 % 75 % 100 %
Einbruch 1.432,00 2.681,75 3.416,50 4.392,00 5.183,00
Raubüberfall 363,00 895,75 1.354,50 1.976,50 4.156,00
Diebstahl 4.090,00 7.739,75 9.624,00 12.059,00 40.278,00
Verkehrsdelikte 2.143,00 4.838,25 6.424,50 7.520,75 11.292,00

 

  • Zweites Quartil (50 %) = Median
Einführung in die Statistik

Boxplot (Kastengrafik)

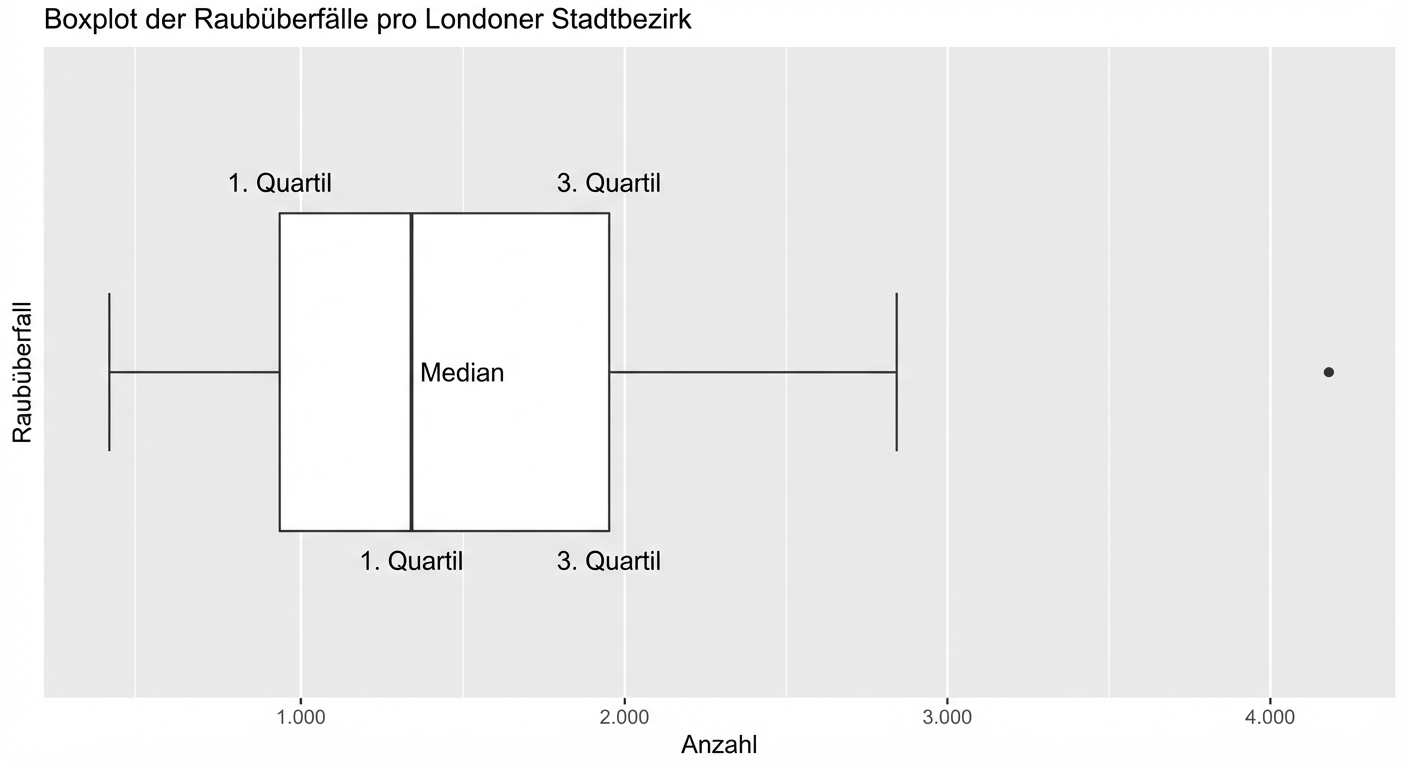
boxplot_of_robberies_in_London_with_median_plus_first_and_third_quartiles_highlighted.png

Einführung in die Statistik

Interquartilsabstand (IQR)

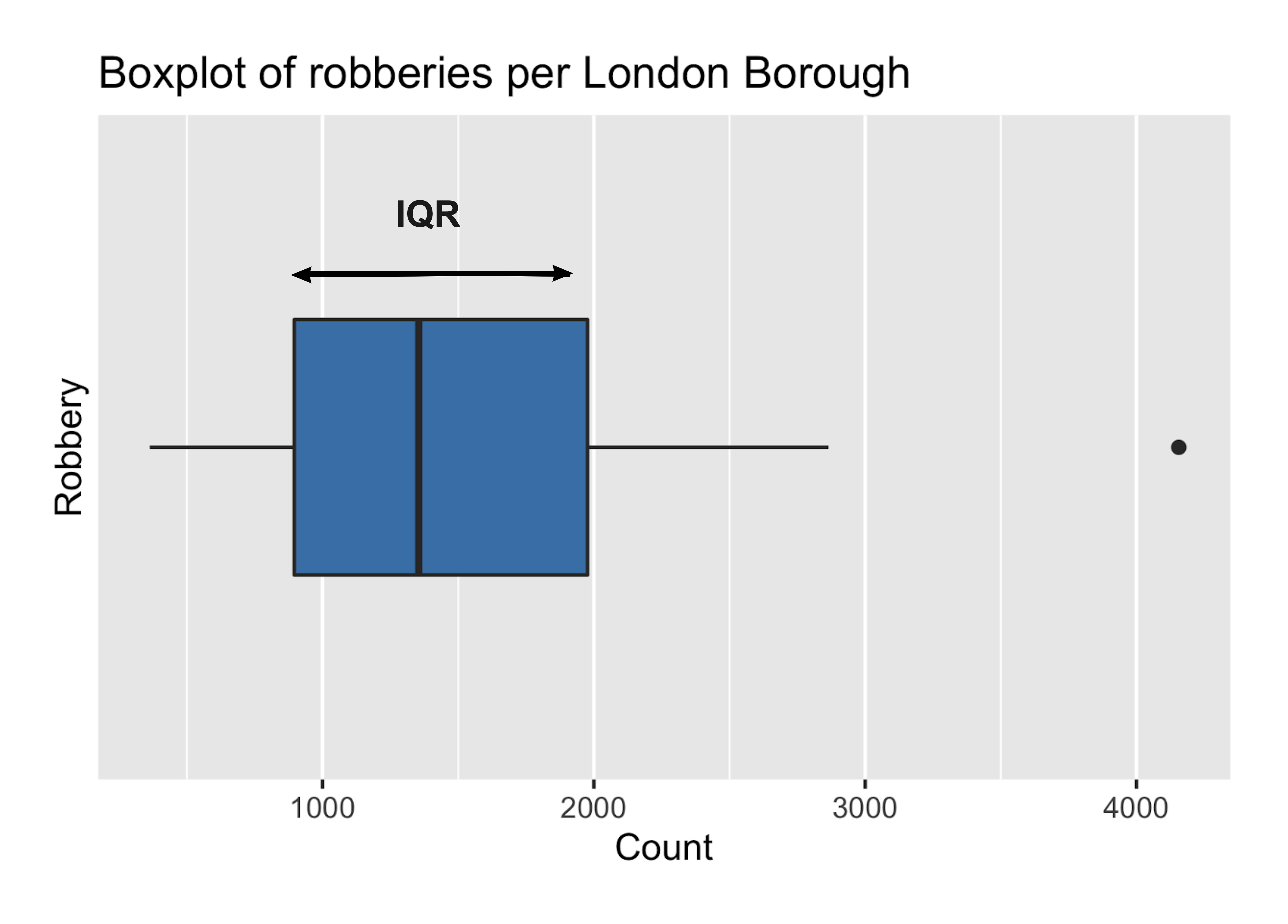
boxplot_robberies_in_London_with_interquartile_range_highlighted.png

  • Der IQR wird weniger von Extremwerten beeinflusst

          IQR = 3. Quartil - 1. Quartil

                IQR = 1.976,50 - 895,75

                       IQR = 1.080,75

Einführung in die Statistik

Lass uns üben!

Einführung in die Statistik

Preparing Video For Download...