Wie stehen die Chancen?

Einführung in die Statistik

George Boorman

Curriculum Manager, DataCamp

Messen von Wahrscheinlichkeiten

Wie hoch ist die Wahrscheinlichkeit eines Ereignisses?

$$ P(\text{Ereignis}) = \frac{\text{\# Ereignis tritt ein}}{\text{\# mögliche Ergebnisse}} $$

Beispiel: Münzwurf

$$ P(\text{Kopf}) = \frac{\text{1 Möglichkeit Kopf zu werfen}}{\text{2 mögliche Ergebnisse}} = \frac{1}{2} = 50\%$$

Wahrscheinlichkeitslinie von links, wo 0 Prozent = unmöglich ist, bis rechts, wo 100 Prozent = wird sicher passieren.png

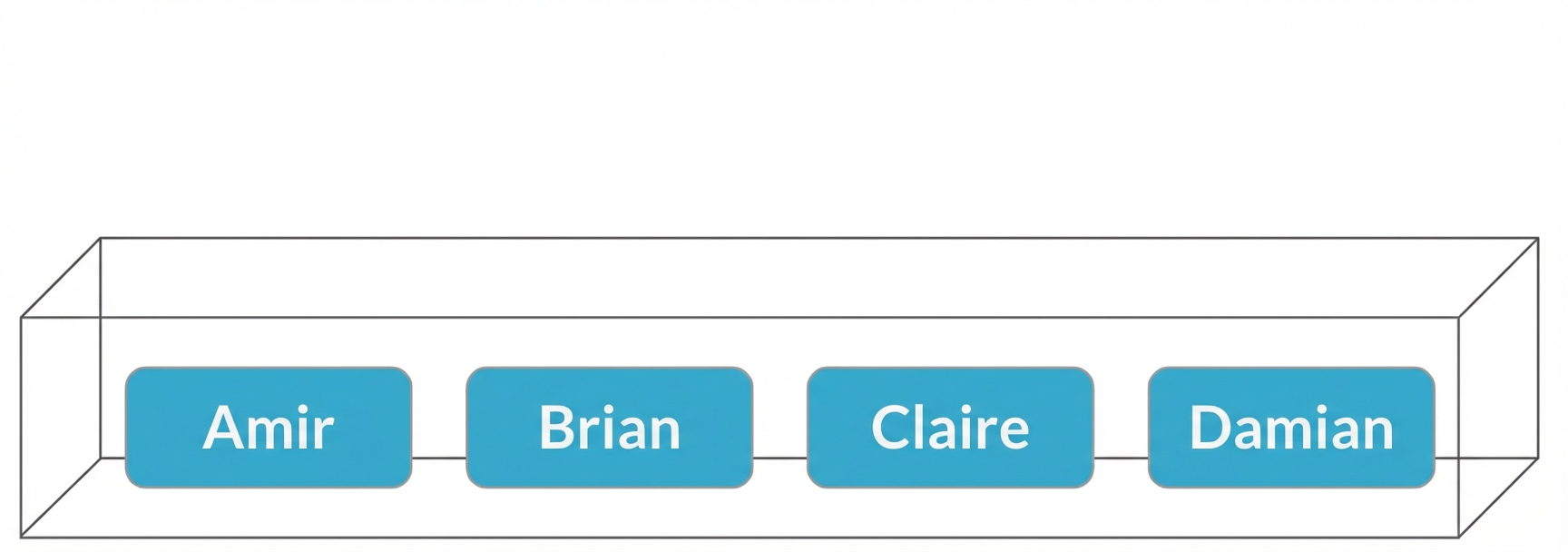
Zuweisung von Vertrieblern

Kasten mit den Namen von Amir, Brian, Claire und Damian.png

Stichproben

Zuweisung von Vertrieblern

Brian's Name aus der Box ziehen.png

$$P(\text{Brian}) = \frac{1}{4} = 25\%$$

Morgenbesprechung

Brian's Name aus der Box ziehen.png

Nachmittagsbesprechung

Brian's Name aus der Box ziehen.png

$$P(\text{Brian}) = \frac{1}{4} = 25\%$$

Stichproben mit Ersatz

Unabhängige Wahrscheinlichkeit

Zwei Ereignisse sind unabhängig, wenn sich die Wahrscheinlichkeit des zweiten Ereignisses nicht aufgrund der Ausgangs des ersten Ereignisses ändert.

Online-Verkäufe im Einzelhandel

Nummer	Typ	Nettomenge	Bruttoumsatz	Rabatt	Retouren	Nettoumsatz
200	Korb	13	3.744,0	-316,80	0,00	3.427,20
201	Korb	12	3.825.0	-201,60	-288,0	3.335,40
202	Korb	17	3.035,0	-63,25	0,00	2.971,75
203	Kunst & Bildhauerei	47	2.696,8	-44,16	0,00	2.652,64
204	Korb	17	2.695,0	-52,50	-110,00	2.532,50

¹ Bildnachweis: https://unsplash.com/@rodriguezedm

Wahrscheinlichkeit einer Bestellung eines Schmuckprodukts

Typ	Anzahl der Bestellungen
Korb	551
Kunst & Bildhauerei	337
Schmuck	210
Küche	161
Wohnungseinrichtung	131
...	...
Gesamt	1767

Wahrscheinlichkeit einer Bestellung eines Schmuckprodukts

$$P(Schmuck) = \frac{Bestellung \ Anzahl(Schmuck)}{Summe(Gesamt \ Bestellung \ Anzahl)}$$

$$P(Schmuck) = \frac{210}{1767}$$

$$P(Schmuck) = 11,88 \%$$

Wahrscheinlichkeiten für alle Produkttypen

Typ	Anzahl der Bestellungen	Wahrscheinlichkeit
Korb	551	31,18 %
Kunst & Bildhauerei	337	19,07 %
Schmuck	210	11,88 %
Küche	161	9,11 %
Wohnungseinrichtung	131	7,41 %
...	...	...
Gesamt	1767	100 %

Lass uns üben!

Einführung in die Statistik