Fitting the Weibull model

Survival Analysis in Python

Shae Wang

Senior Data Scientist

Probability distributions

A probability distribution

A mathematical function that describes the probability of different event outcomes.

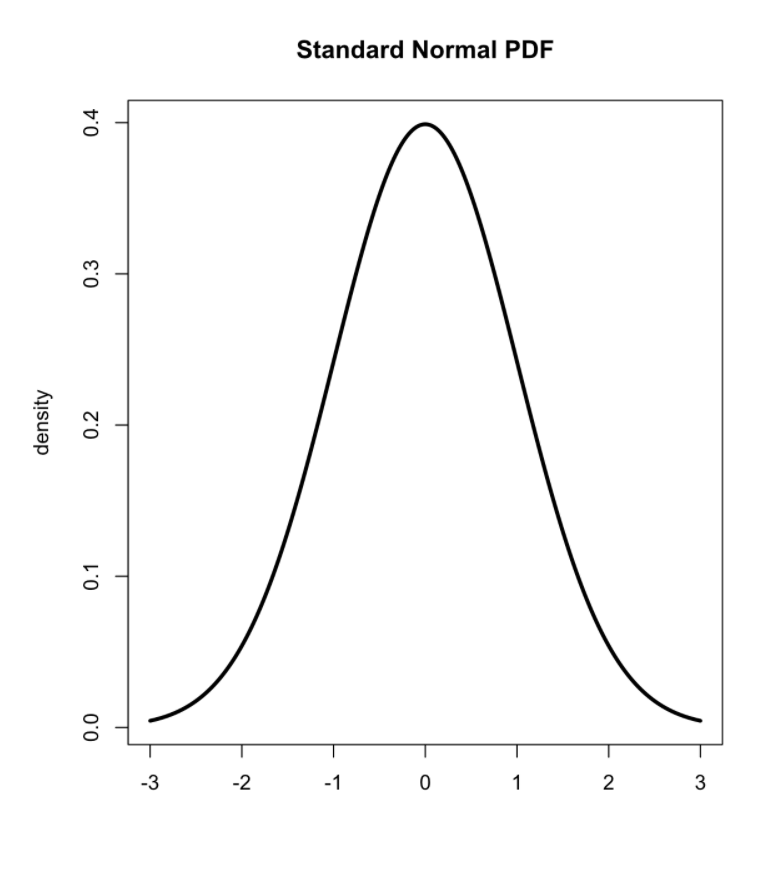
normal distribution

Probability distributions

A probability distribution

A mathematical function that describes the probability of different event outcomes.

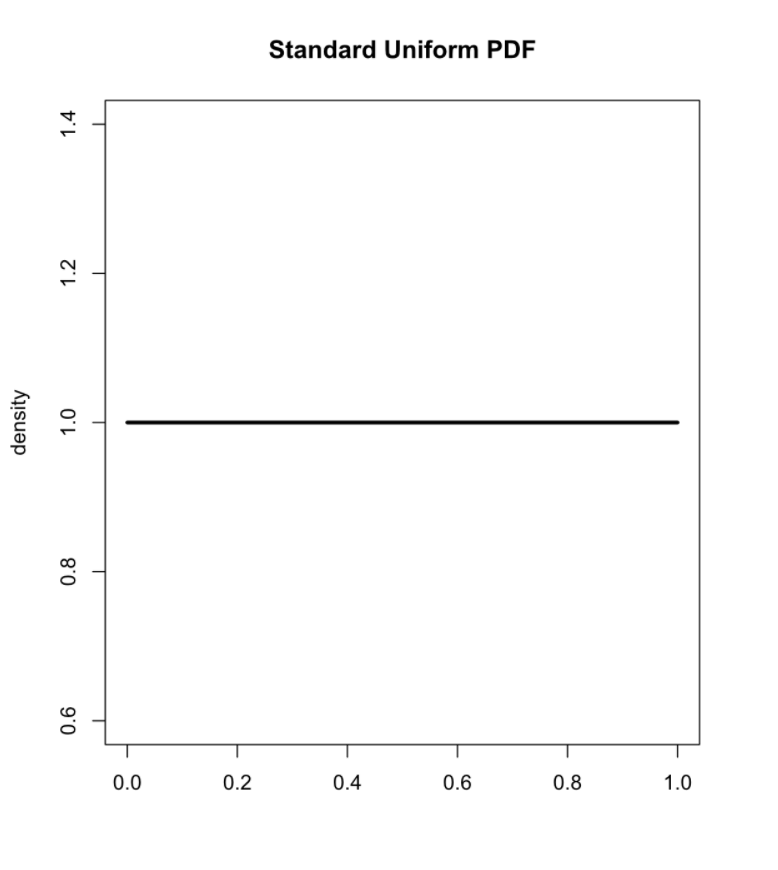
uniform distribution

Introducing the Weibull distribution

The Weibull distribution

A continuous probability distribution that models time-to-event data very well (but originally applied to model particle size distribution).

The Weibull probability density function

$$f(x;\lambda,k)=\frac{k}{\lambda}\bigg(\frac{x}{\lambda}\bigg)^{k-1}e^{-(x/\lambda)^k}$$ $$x\geq0,k>0,\lambda>0$$

Introducing the Weibull distribution

$k$

Determines the shape

varying_k

$\lambda$

Determines the scale

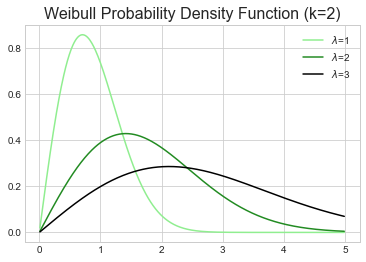
varying_lambda

Fitting the Weibull distribution to data

A company maintains a fleet of machines that are prone to failure...

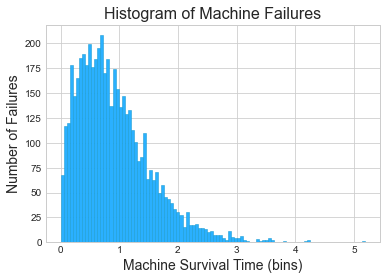
machine_failure_histogram

Fitting the Weibull distribution to data

A company maintains a fleet of machines that are prone to failure...

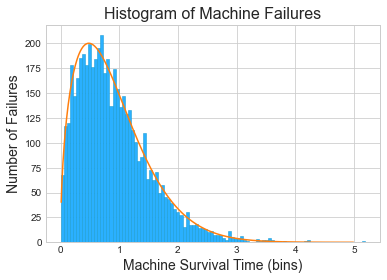
machine_failure_weibull

From Weibull distribution to survival function

$$f(x;\lambda,k)=\frac{k}{\lambda}\bigg(\frac{x}{\lambda}\bigg)^{k-1}e^{-(x/\lambda)^k} \quad\rightarrow\quad\qquad\qquad S(t)=e^{-(t/\lambda)^\rho}$$

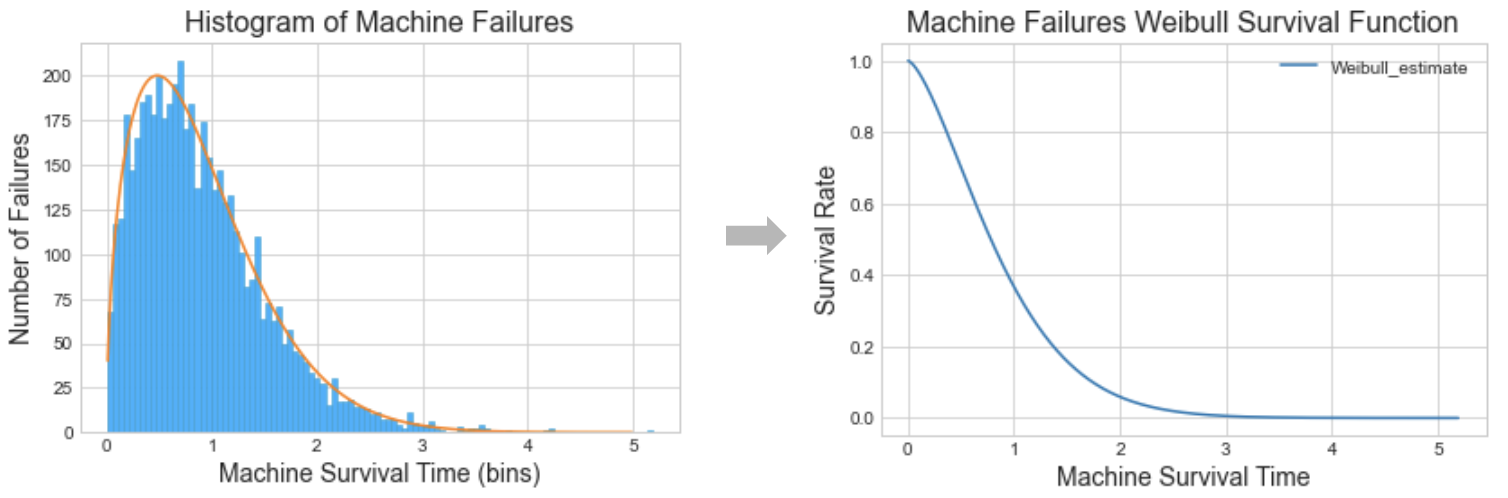
weibull_to_survival_function

$\rho$ is same as k

The knobs: k and lambda

k and $\lambda$

k (or $\rho$): determines the shape
$\lambda$: determines the scale (indicates when 63.2% of the population has experienced the event)

$$f(x;\lambda,k)=\frac{k}{\lambda}\bigg(\frac{x}{\lambda}\bigg)^{k-1}e^{-(x/\lambda)^k} \quad\rightarrow\quad f(x;\lambda,k=3)=\frac{3}{\lambda}\bigg(\frac{x}{\lambda}\bigg)^2e^{-(x/\lambda)^3}$$

Weibull distribution: the failure/event rate is proportional to a power of time.

Interpreting k (or $\rho$)

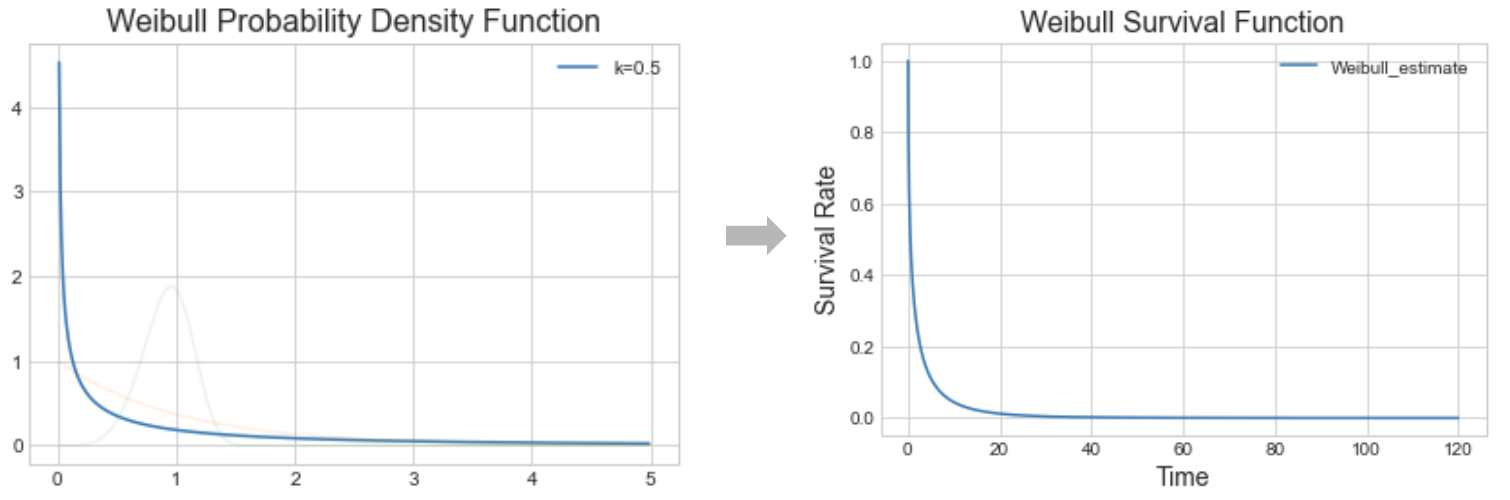
k<1, event rate decreases

When $k<1$, the failure/event rate decreases over time.

Interpreting k (or $\rho$)

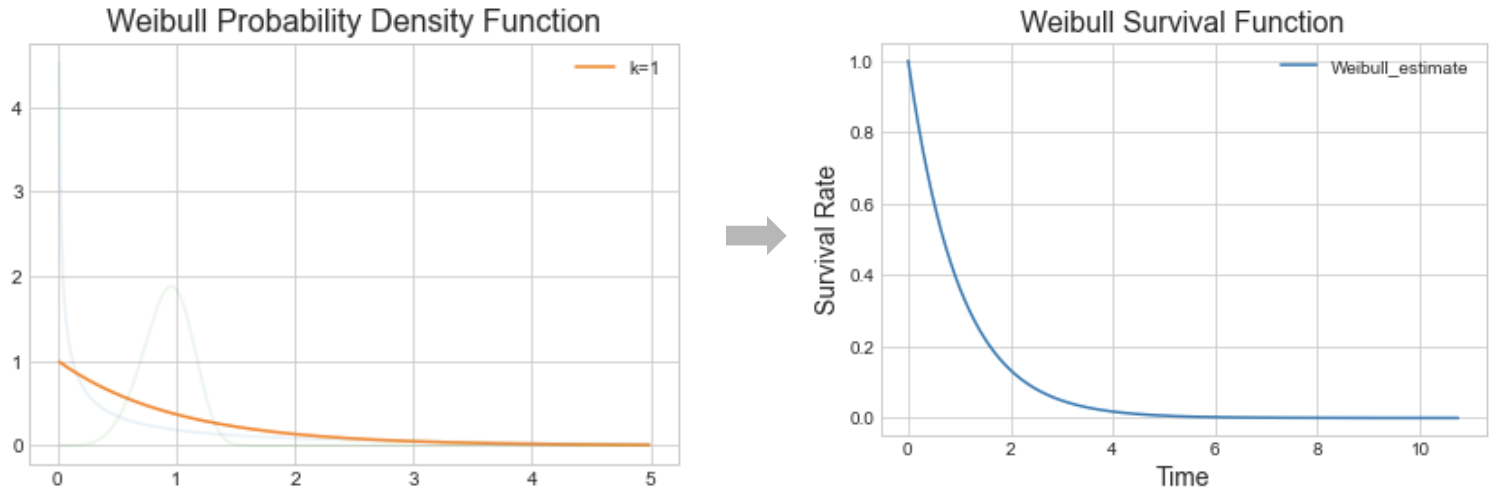
k=1, event rate constant

When $k=1$, the failure/event rate is constant over time.

Interpreting k (or $\rho$)

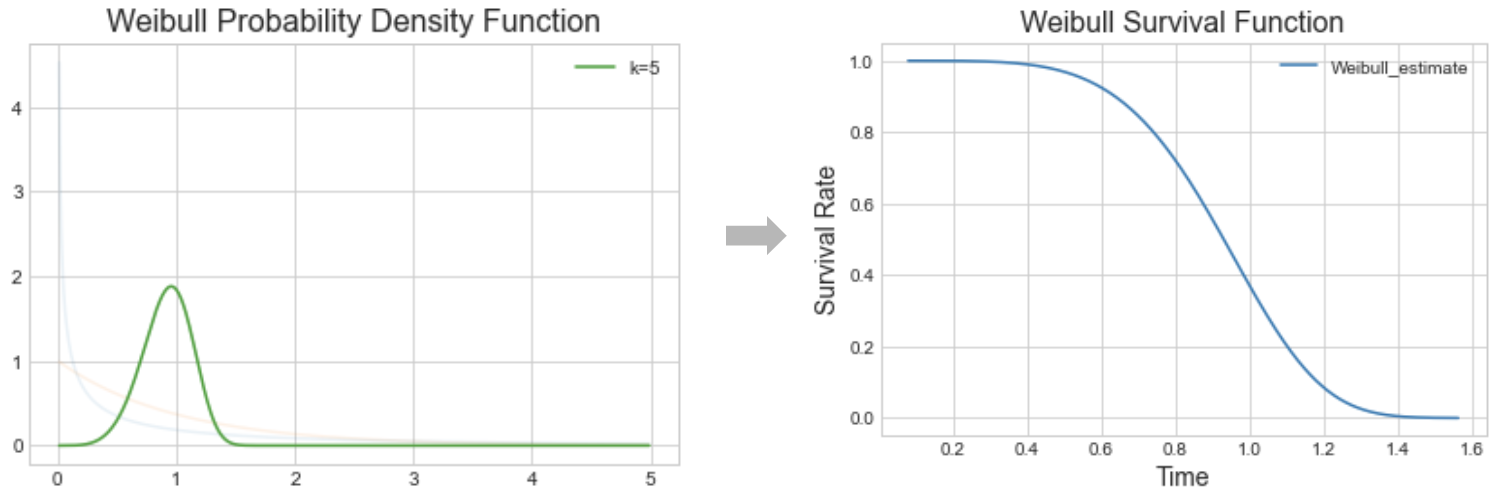
k>1, event rate increases

When $k>1$, the failure/event rate increases over time.

Survival analysis with Weibull distribution

Import the WeibullFitter class
```
from lifelines import WeibullFitter
```
Instantiate a WeibullFitter class
```
wb = WeibullFitter()
```
Call .fit() to fit the estimator to the data
```
wb.fit(durations, event_observed)
```
Access .survival_function_, .lambda_, .rho_, .summary, .predict()

Example Weibull model

DataFrame name: mortgage_df

id	duration	paid_off
1	25	0
2	17	1
3	5	0
...	...	...
1000	30	1

from lifelines import WeibullFitter
wb = WeibullFitter()

wb.fit(durations=mortgage_df["duration"],
       event_observed=mortgage_df["paid_off"])

Example Weibull model

wb.survival_function_.plot()
plt.show()

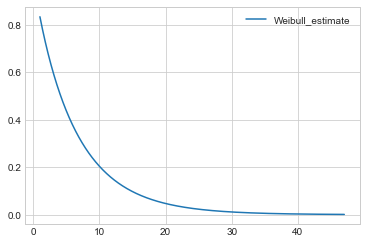
example weibull survival curve

print(wb.lambda_, wb.rho_)

6.11  0.94

print(wb.predict(20))

0.05

Let's practice!

Survival Analysis in Python