Predictions and odds ratios

Introduction to Regression in R

Richie Cotton

Data Evangelist at DataCamp

The ggplot predictions

plt_churn_vs_recency_base <- ggplot(
  churn, 
  aes(time_since_last_purchase, has_churned)
) +
  geom_point() +
  geom_smooth(
    method = "glm", 
    se = FALSE, 
    method.args = list(family = binomial)
  )

A scatter plot of churn versus time since last purchase, with a logistic trend line.

Making predictions

mdl_recency <- glm(
  has_churned ~ time_since_last_purchase, data = churn, family = "binomial"
)

explanatory_data <- tibble(
  time_since_last_purchase = seq(-1, 6, 0.25)
)

prediction_data <- explanatory_data %>% 
  mutate(
    has_churned = predict(mdl_recency, explanatory_data, type = "response")
  )

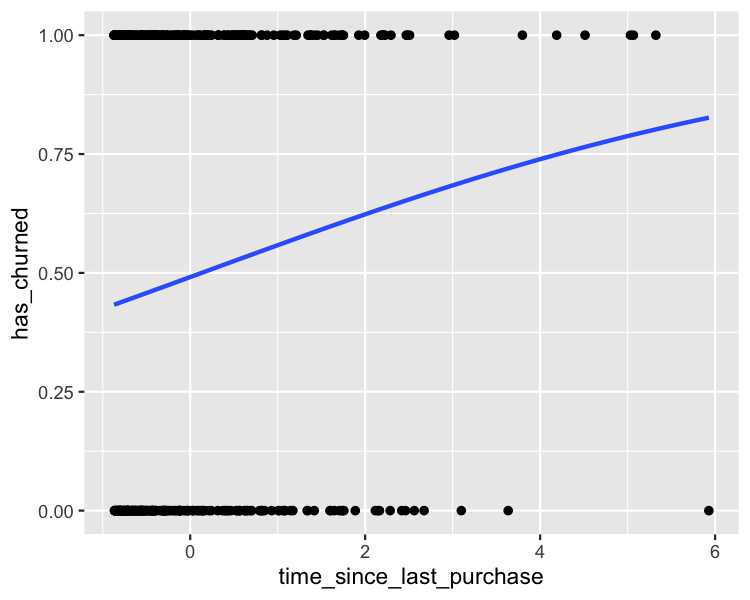
Adding point predictions

plt_churn_vs_recency_base +
  geom_point(
    data = prediction_data, 
    color = "blue"
  )

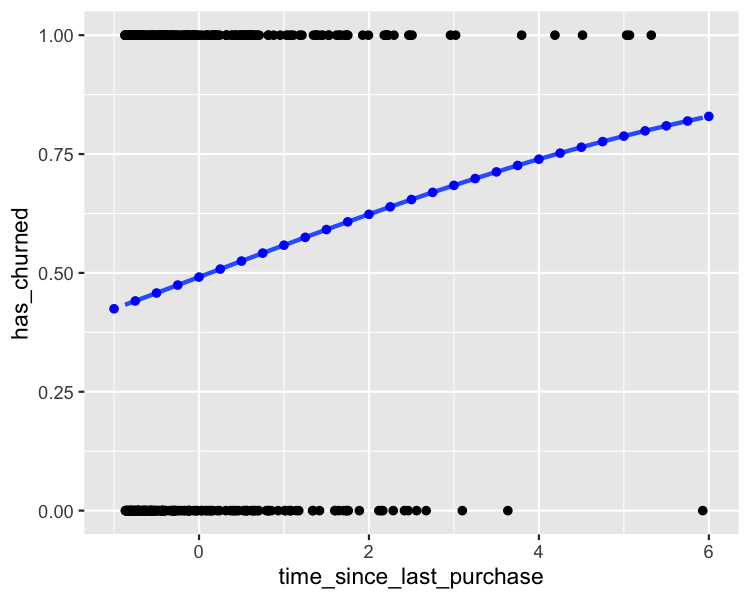
The scatter plot of churn versus time since last purchase, with a logistic trend line. The plot is annotated with the results from predict(), which follow the trend line exactly.

Getting the most likely outcome

prediction_data <- explanatory_data %>% 
  mutate(
    has_churned = predict(mdl_recency, explanatory_data, type = "response"),
    most_likely_outcome = round(has_churned)
  )

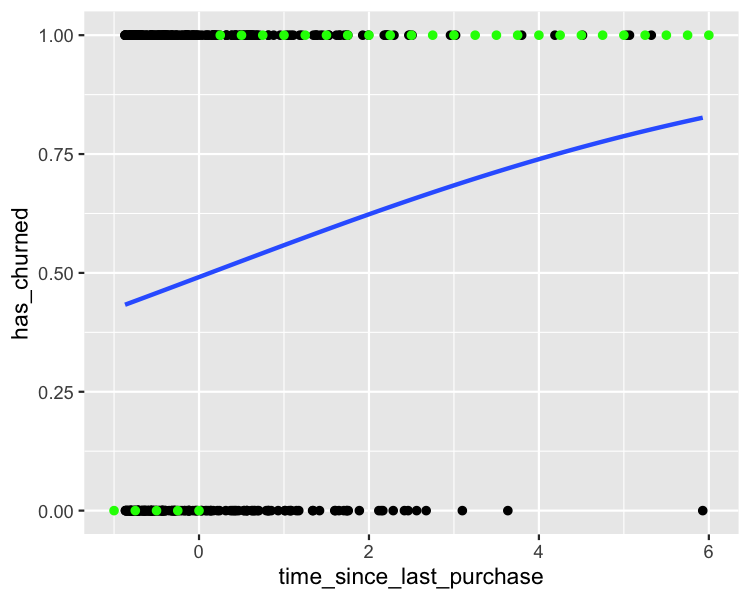
Visualizing most likely outcome

plt_churn_vs_recency_base +
  geom_point(
    aes(y = most_likely_outcome),
    data = prediction_data,
    color = "green"
  )

The scatter plot of churn versus time since last purchase, with a logistic trend line. The plot is annotated with the most likely outcomes. For low time since last purchase, the most likely outcome is not churning. For high time since last purchase, the most likely outcome is churning.

Odds ratios

Odds ratio is the probability of something happening divided by the probability that it doesn't.

$$ odds\_ratio = \frac{probability}{(1 - probability)} $$

$$ odds\_ratio = \frac{0.25}{(1 - 0.25)} = \frac{1}{3} $$

A line plot of odds ratio versus probability. The curve increases asymptotically to infinity as probability tends towards one.

Calculating odds ratio

prediction_data <- explanatory_data %>%
  mutate(
    has_churned = predict(mdl_recency, explanatory_data, type = "response"),
    most_likely_response = round(has_churned),
    odds_ratio = has_churned / (1 - has_churned)
  )

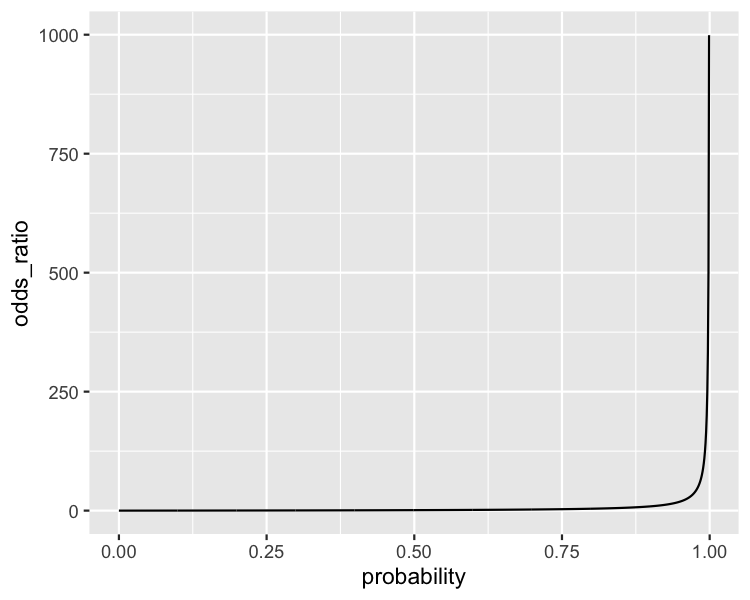
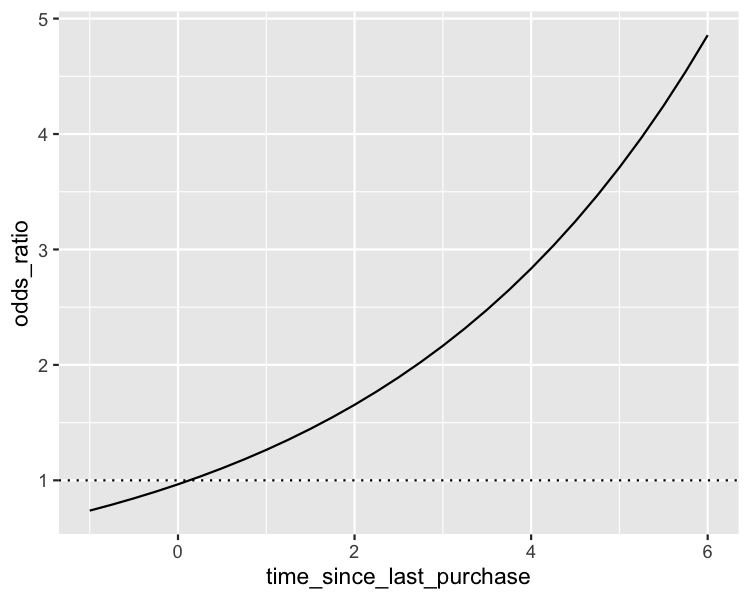
Visualizing odds ratio

ggplot(
  prediction_data, 
  aes(time_since_last_purchase, odds_ratio)
) +
  geom_line() +
  geom_hline(yintercept = 1, linetype = "dotted")

A line plot of odds ratio versus time since last purchase, with a line at odds ratio equals one. For low time since last purchase, the most likely outcome is not churning. The odds of churning increase as time since last purchase increases, up to five time the odds of not churning.

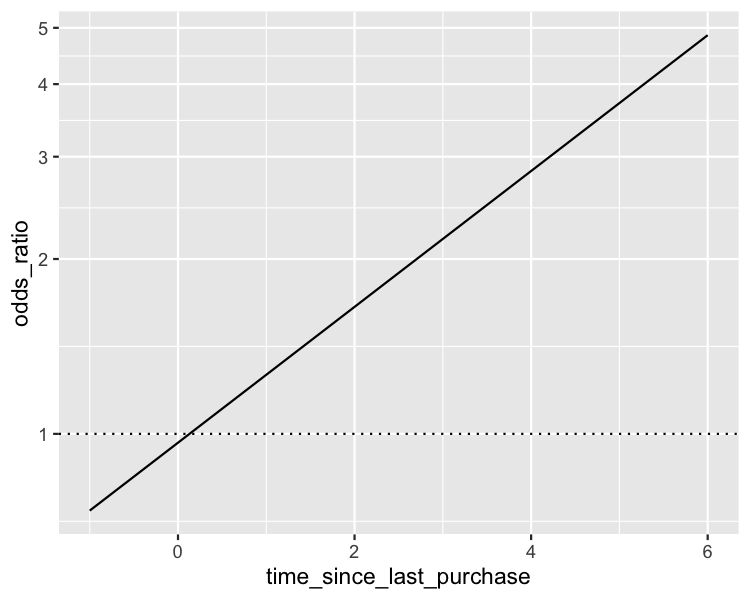
Visualizing log odds ratio

ggplot(
  prediction_data, 
  aes(time_since_last_purchase, odds_ratio)
) +
  geom_line() +
  geom_hline(yintercept = 1, linetype = "dotted") +
  scale_y_log10()

The line plot of odds ratio versus time since last purchase, with a line at odds ratio equals one. The y-axis uses a logarithmic scale, which has resulted in the odds ratio line becoming linear.

Calculating log odds ratio

prediction_data <- explanatory_data %>%
  mutate(
    has_churned = predict(mdl_recency, explanatory_data, type = "response"),
    most_likely_response = round(has_churned),
    odds_ratio = has_churned / (1 - has_churned),
    log_odds_ratio = log(odds_ratio),
    log_odds_ratio2 = predict(mdl_recency, explanatory_data)
  )

All predictions together

tm_snc_lst_prch	has_churned	most_lkly_rspns	odds_ratio	log_odds_ratio	log_odds_ratio2
0	0.491	0	0.966	-0.035	-0.035
2	0.623	1	1.654	0.503	0.503
4	0.739	1	2.834	1.042	1.042
6	0.829	1	4.856	1.580	1.580
...	...	...	...	...	...

Comparing scales

Scale	Are values easy to interpret?	Are changes easy to interpret?	Is precise?
Probability	✔	✘	✔
Most likely outcome	✔✔	✔	✘
Odds ratio	✔	✘	✔
Log odds ratio	✘	✔	✔

Let's practice!

Introduction to Regression in R