ANOVA tests
Hypothesis Testing in Python

James Chapman
Curriculum Manager, DataCamp
Job satisfaction: 5 categories
stack_overflow['job_sat'].value_counts()
Very satisfied 879
Slightly satisfied 680
Slightly dissatisfied 342
Neither 201
Very dissatisfied 159
Name: job_sat, dtype: int64
Visualizing multiple distributions
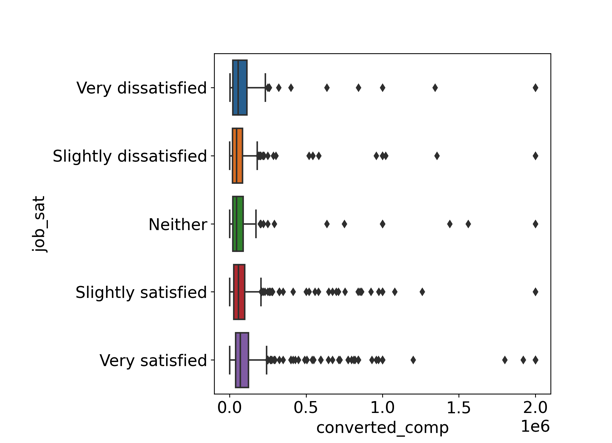
Is mean annual compensation different for different levels of job satisfaction?
import seaborn as sns
import matplotlib.pyplot as plt
sns.boxplot(x="converted_comp",
y="job_sat",
data=stack_overflow)
plt.show()
Analysis of variance (ANOVA)
- A test for differences between groups
alpha = 0.2pingouin.anova(data=stack_overflow, dv="converted_comp", between="job_sat")
Source ddof1 ddof2 F p-unc np2
0 job_sat 4 2256 4.480485 0.001315 0.007882
0.001315$< \alpha$- At least two categories have significantly different compensation
Pairwise tests
- $\mu_{\text{very dissatisfied}} \neq \mu_{\text{slightly dissatisfied}}$
- $\mu_{\text{very dissatisfied}} \neq \mu_{\text{neither}}$
- $\mu_{\text{very dissatisfied}} \neq \mu_{\text{slightly satisfied}}$
- $\mu_{\text{very dissatisfied}} \neq \mu_{\text{very satisfied}}$
- $\mu_{\text{slightly dissatisfied}} \neq \mu_{\text{neither}}$
- $\mu_{\text{slightly dissatisfied}} \neq \mu_{\text{slightly satisfied}}$
- $\mu_{\text{slightly dissatisfied}} \neq \mu_{\text{very satisfied}}$
- $\mu_{\text{neither}} \neq \mu_{\text{slightly satisfied}}$
- $\mu_{\text{neither}} \neq \mu_{\text{very satisfied}}$
- $\mu_{\text{slightly satisfied}} \neq \mu_{\text{very satisfied}}$
Set significance level to $\alpha = 0.2$.
pairwise_tests()
pingouin.pairwise_tests(data=stack_overflow,
dv="converted_comp",
between="job_sat",
padjust="none")
Contrast A B Paired Parametric ... dof alternative p-unc BF10 hedges
0 job_sat Slightly satisfied Very satisfied False True ... 1478.622799 two-sided 0.000064 158.564 -0.192931
1 job_sat Slightly satisfied Neither False True ... 258.204546 two-sided 0.484088 0.114 -0.068513
2 job_sat Slightly satisfied Very dissatisfied False True ... 187.153329 two-sided 0.215179 0.208 -0.145624
3 job_sat Slightly satisfied Slightly dissatisfied False True ... 569.926329 two-sided 0.969491 0.074 -0.002719
4 job_sat Very satisfied Neither False True ... 328.326639 two-sided 0.097286 0.337 0.120115
5 job_sat Very satisfied Very dissatisfied False True ... 221.666205 two-sided 0.455627 0.126 0.063479
6 job_sat Very satisfied Slightly dissatisfied False True ... 821.303063 two-sided 0.002166 7.43 0.173247
7 job_sat Neither Very dissatisfied False True ... 321.165726 two-sided 0.585481 0.135 -0.058537
8 job_sat Neither Slightly dissatisfied False True ... 367.730081 two-sided 0.547406 0.118 0.055707
9 job_sat Very dissatisfied Slightly dissatisfied False True ... 247.570187 two-sided 0.259590 0.197 0.119131
[10 rows x 11 columns]
As the number of groups increases...
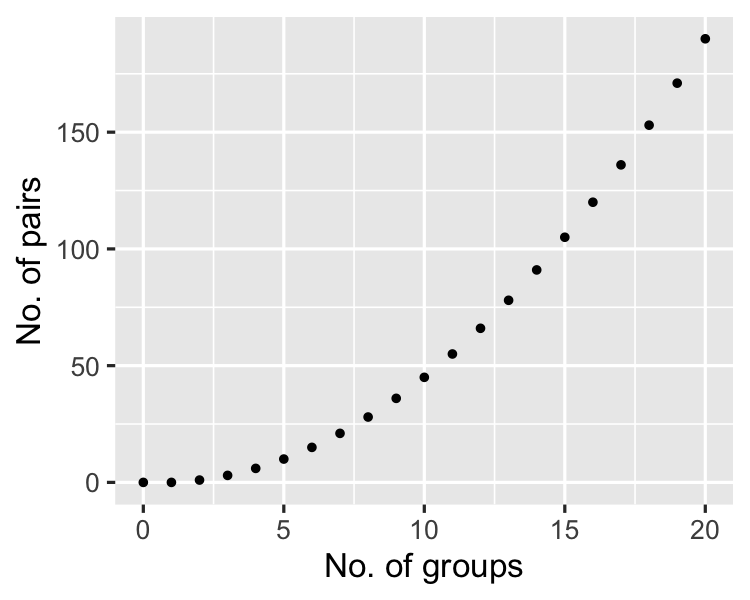
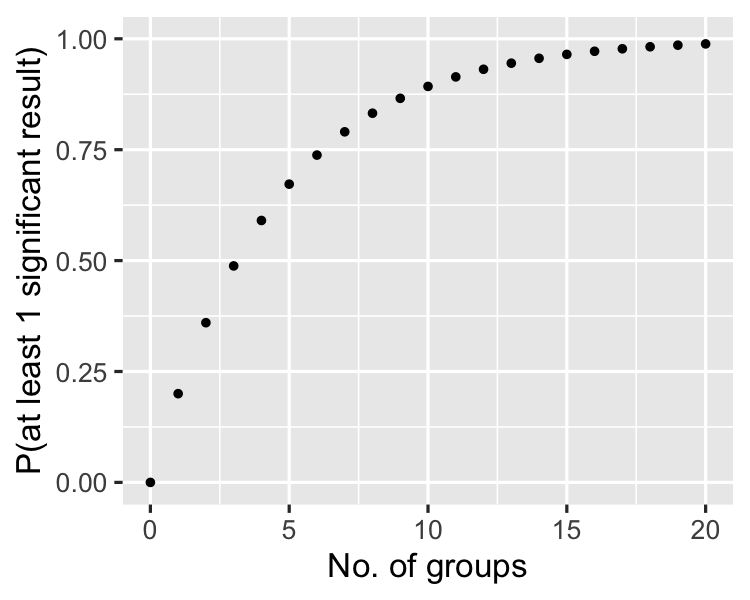
Bonferroni correction
pingouin.pairwise_tests(data=stack_overflow,
dv="converted_comp",
between="job_sat",
padjust="bonf")
Contrast A B ... p-unc p-corr p-adjust BF10 hedges
0 job_sat Slightly satisfied Very satisfied ... 0.000064 0.000638 bonf 158.564 -0.192931
1 job_sat Slightly satisfied Neither ... 0.484088 1.000000 bonf 0.114 -0.068513
2 job_sat Slightly satisfied Very dissatisfied ... 0.215179 1.000000 bonf 0.208 -0.145624
3 job_sat Slightly satisfied Slightly dissatisfied ... 0.969491 1.000000 bonf 0.074 -0.002719
4 job_sat Very satisfied Neither ... 0.097286 0.972864 bonf 0.337 0.120115
5 job_sat Very satisfied Very dissatisfied ... 0.455627 1.000000 bonf 0.126 0.063479
6 job_sat Very satisfied Slightly dissatisfied ... 0.002166 0.021659 bonf 7.43 0.173247
7 job_sat Neither Very dissatisfied ... 0.585481 1.000000 bonf 0.135 -0.058537
8 job_sat Neither Slightly dissatisfied ... 0.547406 1.000000 bonf 0.118 0.055707
9 job_sat Very dissatisfied Slightly dissatisfied ... 0.259590 1.000000 bonf 0.197 0.119131
[10 rows x 11 columns]
More methods
padjust : string
Method used for testing and adjustment of pvalues.
'none': no correction [default]'bonf': one-step Bonferroni correction'sidak': one-step Sidak correction'holm': step-down method using Bonferroni adjustments'fdr_bh': Benjamini/Hochberg FDR correction'fdr_by': Benjamini/Yekutieli FDR correction
Let's practice!
Hypothesis Testing in Python

