Quantifying model fit

Introduction to Regression with statsmodels in Python

Maarten Van den Broeck

Content Developer at DataCamp

Bream and perch models

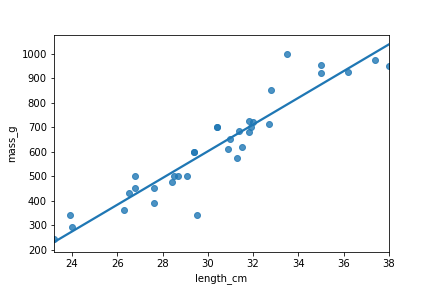
Bream The scatter plot of bream masses versus their lengths, with a trend line, that has been shown previously.

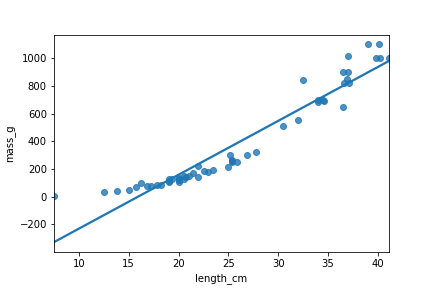
Perch The scatter plot of perch masses versus their lengths, with a trend line, that has been shown previously.

Introduction to Regression with statsmodels in Python

Coefficient of determination

Sometimes called "r-squared" or "R-squared".

The proportion of the variance in the response variable that is predictable from the explanatory variable

  • 1 means a perfect fit
  • 0 means the worst possible fit
Introduction to Regression with statsmodels in Python

.summary()

Look at the value titled "R-Squared"

mdl_bream = ols("mass_g ~ length_cm", data=bream).fit()

print(mdl_bream.summary())

# Some lines of output omitted                          

                            OLS Regression Results                         
Dep. Variable:                 mass_g   R-squared:                       0.878
Model:                            OLS   Adj. R-squared:                  0.874
Method:                 Least Squares   F-statistic:                     237.6
Introduction to Regression with statsmodels in Python

.rsquared attribute

print(mdl_bream.rsquared)

0.8780627095147174
Introduction to Regression with statsmodels in Python

It's just correlation squared

coeff_determination = bream["length_cm"].corr(bream["mass_g"]) ** 2
print(coeff_determination)

0.8780627095147173
Introduction to Regression with statsmodels in Python

Residual standard error (RSE)

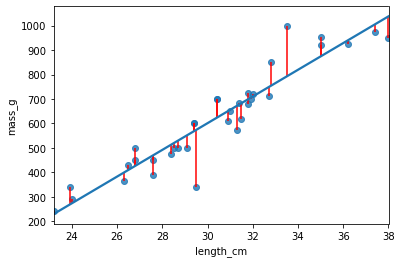
Residuals of the bream mass vs length scatter plot, as seen before

  • A "typical" difference between a prediction and an observed response
  • It has the same unit as the response variable.
  • MSE = RSE²
Introduction to Regression with statsmodels in Python

.mse_resid attribute

mse = mdl_bream.mse_resid
print('mse: ', mse)

mse:  5498.555084973521

rse = np.sqrt(mse)
print("rse: ", rse)

rse:  74.15224261594197
Introduction to Regression with statsmodels in Python

Calculating RSE: residuals squared

residuals_sq = mdl_bream.resid ** 2

print("residuals sq: \n", residuals_sq)

residuals sq: 
0      138.957118
1      260.758635
2     5126.992578
3     1318.919660
4      390.974309
    ...
30    2125.047026
31    6576.923291
32     206.259713
33     889.335096
34    7665.302003
Length: 35, dtype: float64
Introduction to Regression with statsmodels in Python

Calculating RSE: sum of residuals squared

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

print("resid sum of sq :",
      resid_sum_of_sq)

resid sum of sq : 181452.31780412616
Introduction to Regression with statsmodels in Python

Calculating RSE: degrees of freedom

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

deg_freedom = len(bream.index) - 2

print("deg freedom: ", deg_freedom)

Degrees of freedom equals the number of observations minus the number of model coefficients.

deg freedom:  33
Introduction to Regression with statsmodels in Python

Calculating RSE: square root of ratio

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

deg_freedom = len(bream.index) - 2

rse = np.sqrt(resid_sum_of_sq/deg_freedom)

print("rse :", rse)

rse : 74.15224261594197
Introduction to Regression with statsmodels in Python

Interpreting RSE

mdl_bream has an RSE of 74.

The difference between predicted bream masses and observed bream masses is typically about 74g.

Introduction to Regression with statsmodels in Python

Root-mean-square error (RMSE)

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

deg_freedom = len(bream.index) - 2

rse = np.sqrt(resid_sum_of_sq/deg_freedom)

print("rse :", rse)

rse : 74.15224261594197

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

n_obs = len(bream.index)

rmse = np.sqrt(resid_sum_of_sq/n_obs)

print("rmse :", rmse)

rmse : 72.00244396727619
Introduction to Regression with statsmodels in Python

Let's practice!

Introduction to Regression with statsmodels in Python

Preparing Video For Download...