Transforming variables

Introduction to Regression with statsmodels in Python

Maarten Van den Broeck

Content Developer at DataCamp

Perch dataset

perch = fish[fish["species"] == "Perch"]
print(perch.head())

   species  mass_g  length_cm
55   Perch     5.9        7.5
56   Perch    32.0       12.5
57   Perch    40.0       13.8
58   Perch    51.5       15.0
59   Perch    70.0       15.7

European perch, _Perca fluviatilis_

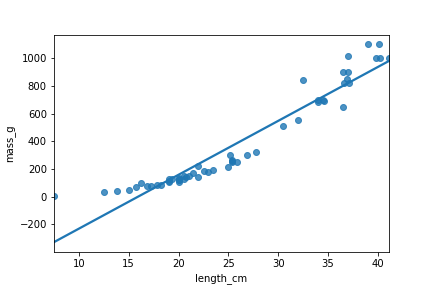
It's not a linear relationship

sns.regplot(x="length_cm",
            y="mass_g",
            data=perch,
            ci=None)

plt.show()

A scatter plot of perch masses versus their lengths, with a trend line. The perches get heavier faster than linearly as they get longer, resulting in an upward curve.

Bream vs. perch

A common bream. Bream are quite flat.

A European perch. Perch are quite round.

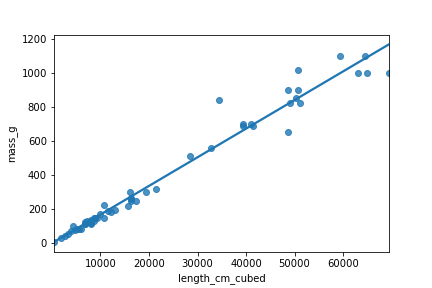
Plotting mass vs. length cubed

perch["length_cm_cubed"] = perch["length_cm"] ** 3

sns.regplot(x="length_cm_cubed",
            y="mass_g",
            data=perch,
            ci=None)
plt.show()

A scatter plot of perch masses versus their lengths cubed, with a trend line. After this transformation, the points are mostly close to the trend line.

Modeling mass vs. length cubed

perch["length_cm_cubed"] = perch["length_cm"] ** 3

mdl_perch = ols("mass_g ~ length_cm_cubed", data=perch).fit()
mdl_perch.params

Intercept         -0.117478
length_cm_cubed    0.016796
dtype: float64

Predicting mass vs. length cubed

explanatory_data = pd.DataFrame({"length_cm_cubed": np.arange(10, 41, 5) ** 3,
                                 "length_cm": np.arange(10, 41, 5)})

prediction_data = explanatory_data.assign(
  mass_g=mdl_perch.predict(explanatory_data))
print(prediction_data)

   length_cm_cubed  length_cm       mass_g
0             1000         10    16.678135
1             3375         15    56.567717
2             8000         20   134.247429
3            15625         25   262.313982
4            27000         30   453.364084
5            42875         35   719.994447
6            64000         40  1074.801781

Plotting mass vs. length cubed

fig = plt.figure()
sns.regplot(x="length_cm_cubed", y="mass_g",
            data=perch, ci=None)
sns.scatterplot(data=prediction_data,
                x="length_cm_cubed", y="mass_g",
                color="red", marker="s")

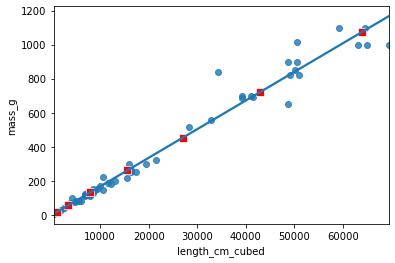
The scatter plot of perch masses versus their lengths cubed, with a trend line, annotated with points calculated from the predict() function. The points follow the trend line exactly.

fig = plt.figure()
sns.regplot(x="length_cm", y="mass_g",
            data=perch, ci=None)
sns.scatterplot(data=prediction_data,
                x="length_cm", y="mass_g",
                color="red", marker="s")

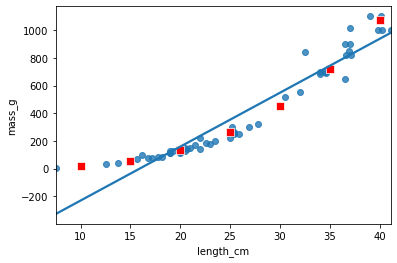
The scatter plot of perch masses versus their lengths, with a trend line, annotated with points calculated from the predict() function. The points don't follow the trend line but they do follow the curve of the data points.

Facebook advertising dataset

How advertising works

Pay Facebook to shows ads.
People see the ads ("impressions").
Some people who see it, click it.

936 rows
Each row represents 1 advert

spent_usd	n_impressions	n_clicks
1.43	7350	1
1.82	17861	2
1.25	4259	1
1.29	4133	1
4.77	15615	3
...	...	...

Plot is cramped

sns.regplot(x="spent_usd",
            y="n_impressions",
            data=ad_conversion,
            ci=None)

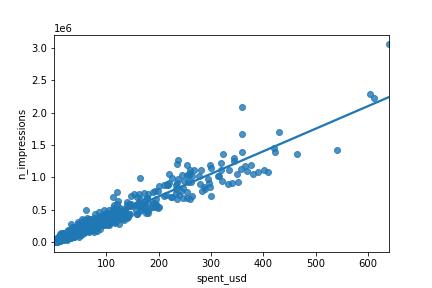
A scatter plot of number of impressions versus advertising spend, with a trend line. Most data points are crammed into the bottom left of the plot.

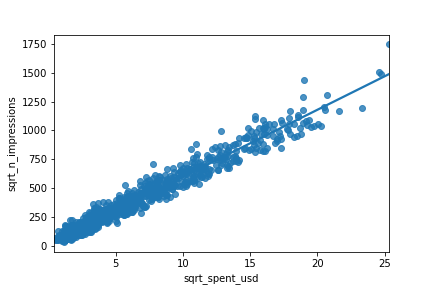
Square root vs square root

ad_conversion["sqrt_spent_usd"] = np.sqrt(
  ad_conversion["spent_usd"])

ad_conversion["sqrt_n_impressions"] = np.sqrt(
  ad_conversion["n_impressions"])

sns.regplot(x="sqrt_spent_usd",
            y="sqrt_n_impressions",
            data=ad_conversion,
            ci=None)

A scatter plot of the square root of the number of impressions versus the square root of the advertising spend, with a trend line. Now the points are more evenly spread throughout the plot.

Modeling and predicting

mdl_ad = ols("sqrt_n_impressions ~ sqrt_spent_usd", data=ad_conversion).fit()

explanatory_data = pd.DataFrame({"sqrt_spent_usd": np.sqrt(np.arange(0, 601, 100)),
                                 "spent_usd": np.arange(0, 601, 100)})

prediction_data = explanatory_data.assign(sqrt_n_impressions=mdl_ad.predict(explanatory_data),
                          n_impressions=mdl_ad.predict(explanatory_data) ** 2)
print(prediction_data)

   sqrt_spent_usd  spent_usd  sqrt_n_impressions  n_impressions
0        0.000000          0           15.319713   2.346936e+02
1       10.000000        100          597.736582   3.572890e+05
2       14.142136        200          838.981547   7.038900e+05
3       17.320508        300         1024.095320   1.048771e+06
4       20.000000        400         1180.153450   1.392762e+06
5       22.360680        500         1317.643422   1.736184e+06
6       24.494897        600         1441.943858   2.079202e+06

Let's practice!

Introduction to Regression with statsmodels in Python