One-sample proportion tests

Hypothesis Testing in R

Richie Cotton

Data Evangelist at DataCamp

Chapter 1 recap

Is a claim about an unknown population proportion feasible?
Standard error of sample statistic calculated using bootstrap distribution.
This was used to compute a standardized test statistic, ...
which was used to calculate a p-value, ...
which was used to decide which hypothesis made most sense.
Here, we'll calculate the test statistic without using the bootstrap distribution.

Standardized test statistic for proportions

$p$: population proportion (unknown population parameter)

$\hat{p}$: sample proportion (sample statistic)

$p_{0}$: hypothesized population proportion

$$ z = \frac{\hat{p} - \text{mean}(\hat{p})}{\text{standard error}(\hat{p})} = \frac{\hat{p} - p}{\text{standard error}(\hat{p})} $$

Assuming $H_{0}$ is true, $p = p_{0}$, so

$$ z = \dfrac{\hat{p} - p_{0}}{\text{standard error}(\hat{p})} $$

Easier standard error calculations

$SE(\bar{x}_{\text{child}} - \bar{x}_{\text{adult}}) \approx \sqrt{\dfrac{s_{\text{child}}^2}{n_{\text{child}}} + \dfrac{s_{\text{adult}}^2}{n_{\text{adult}}}}$

$SE_{\hat{p}} = \sqrt{\dfrac{p_{0}*(1-p_{0})}{n}}$

Assuming $H_{0}$ is true,

$z = \dfrac{\hat{p} - p_{0}}{\sqrt{\dfrac{p_{0}*(1-p_{0})}{n}}}$

This only uses sample information ($\hat{p}$ and $n$) and the hypothesized parameter ($p_{0}$).

Why z instead of t?

$t = \dfrac{(\bar{x}_{\text{child}} - \bar{x}_{\text{adult}})}{\sqrt{\dfrac{s_{\text{child}}^2}{n_{\text{child}}} + \dfrac{s_{\text{adult}}^2}{n_{\text{adult}}}}}$

$s$ is calculated from $\bar{x}$, so $\bar{x}$ is used to estimate the population mean and to estimate the population standard deviation.
This increases uncertainty in our estimate of the population parameter.
t-distribution has fatter tails than a normal distribution.
This gives an extra level of caution.
$\hat{p}$ only appears in the numerator, so z-scores are fine.

Stack Overflow age categories

$H_{0}$: The proportion of SO users under thirty is equal to 0.5.

$H_{A}$: The proportion of SO users under thirty is not equal to 0.5.

alpha <- 0.01

stack_overflow %>% 
  count(age_cat)

# A tibble: 2 x 2
  age_cat         n
  <chr>       <int>
1 At least 30  1050
2 Under 30     1216

Variables for z

p_hat <- stack_overflow %>%
  summarize(prop_under_30 = mean(age_cat == "Under 30")) %>%
  pull(prop_under_30)

0.5366

p_0 <- 0.50

n <- nrow(stack_overflow)

Calculating the z-score

$z = \dfrac{\hat{p} - p_{0}}{\sqrt{\dfrac{p_{0}*(1-p_{0})}{n}}}$

numerator <- p_hat - p_0
denominator <- sqrt(p_0 * (1 - p_0) / n)
z_score <- numerator / denominator

3.487

Calculating the p-value

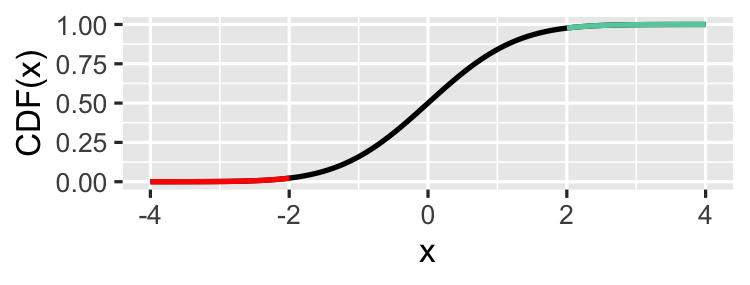CDF of the normal distribution. The part of the line that's less than -2 is in red and the part of the line that's more than 2 is in green. Left-tailed ("less than")

p_value <- pnorm(z_score)

Right-tailed ("greater than")

p_value <- pnorm(z_score, lower.tail = FALSE)

Two-tailed ("not equal")

p_value <- pnorm(z_score) + 
  pnorm(z_score, lower.tail = FALSE)

p_value <- 2 * pnorm(z_score)

0.000244

p_value <= alpha

TRUE

Let's practice!

Hypothesis Testing in R