Calculating p-values from t-statistics

Hypothesis Testing in R

Richie Cotton

Data Evangelist at DataCamp

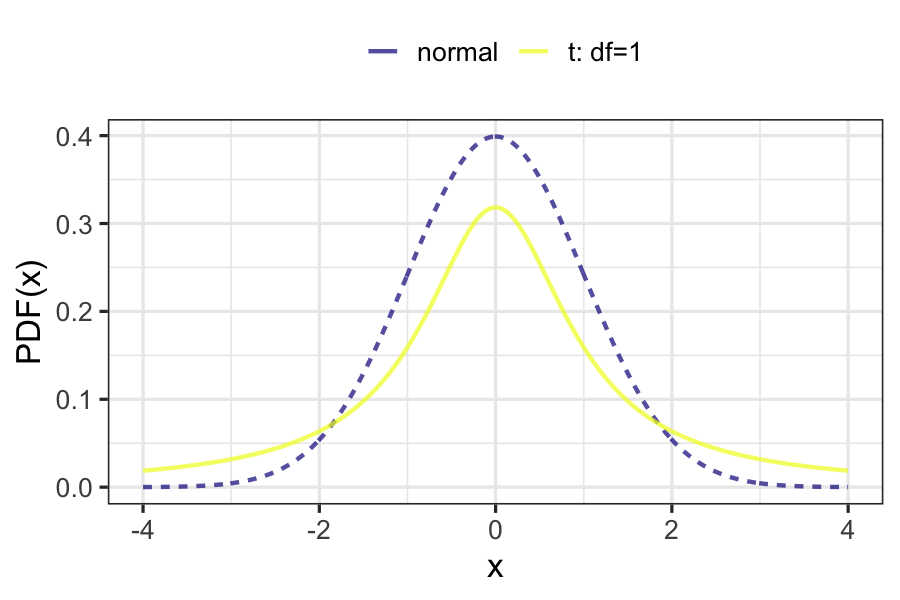
t-distributions

The test statistic, t, follows a t-distribution.
t-distributions have a parameter named degrees of freedom, or df.
t-distributions look like normal distributions, with fatter tails.

Graph showing the PDF of a standard normal distribution compared to a t-distribution with 1 degree of freedom. The t-distribution has fatter tails and a shorter peak in the middle.

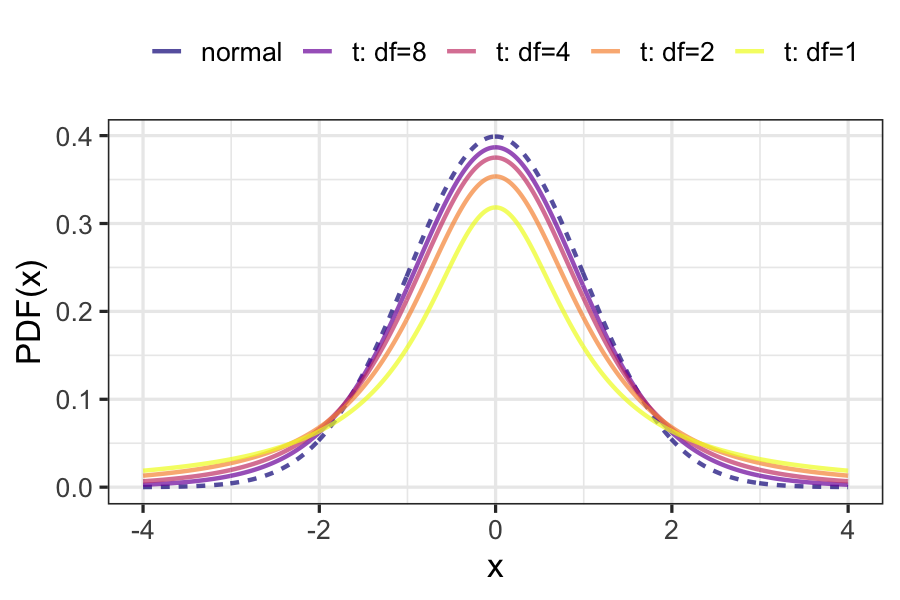
Degrees of freedom

As you increase the degrees of freedom, the t-distribution gets closer to the normal distribution.
A normal distribution is a t-distribution with infinite degrees of freedom.
Degrees of freedom are the maximum number of logically independent values in the data sample.

Graph showing the PDF of a standard normal distribution compared to a t-distribution with various degrees of freedom. As degrees of freedom increases, the tails get narrower and the peak gets higher, more closely resembling the normal distribution.

Calculating degrees of freedom

Suppose your dataset has 5 independent observations.
Four of the values are 2, 6, 8, and 5.
You also know the sample mean is 5.
The last value is no longer independent; it must be 4.
There are 4 degrees of freedom.
$df = n_{child} + n_{adult} - 2$

Hypotheses

$H_{0}$: The mean compensation (in USD) is the same for those that coded first as a child and those that coded first as an adult.

$H_{A}$: The mean compensation (in USD) is greater for those that coded first as a child compared to those that coded first as an adult.

Use a right-tailed test.

Significance level

$\alpha = 0.1$

If $p \le \alpha$ then reject $H_{0}$.

Calculating p-values: one proportion vs. a value

p_value <- pnorm(z_score, lower.tail = FALSE)

Calculating p-values: two means from different groups

numerator <- xbar_child - xbar_adult
denominator <- sqrt(s_child ^ 2 / n_child + s_adult ^ 2 / n_adult)
t_stat <- numerator / denominator

2.4046

degrees_of_freedom <- n_child + n_adult - 2

Test statistic standard error used an approximation (not bootstrapping).
Use t-distribution CDF not normal CDF.

p_value <- pt(t_stat, df = degrees_of_freedom, lower.tail = FALSE)

0.008130

Let's practice!

Hypothesis Testing in R