Introducing an AR Model

Time Series Analysis in Python

Rob Reider

Adjunct Professor, NYU-Courant Consultant, Quantopian

Mathematical Description of AR(1) Model

$\large \quad \quad \quad \quad R_t \quad \ \ = \quad \mu \quad + \quad \phi \quad R_{t-1} \quad \ + \quad \epsilon_t$

Since only one lagged value on right hand side, this is called:
- AR model of order 1, or
- AR(1) model
AR parameter is $\large \phi$
For stationarity, $\large -1 \lt \phi \lt 1$

Interpretation of AR(1) Parameter

$\large \quad \quad \quad \quad R_t \quad \ \ = \quad \mu \quad + \quad \phi \quad R_{t-1} \quad \ + \quad \epsilon_t$

Negative $\large \phi$: Mean Reversion
Positive $\large \phi$: Momentum

Comparison of AR(1) Time Series

$\large \phi=0.9$
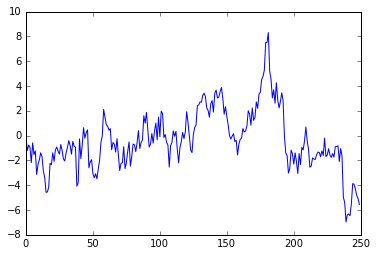
$\large \phi=0.5$

$\large \phi=-0.9$
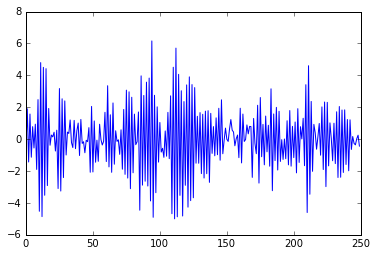
$\large \phi=-0.5$

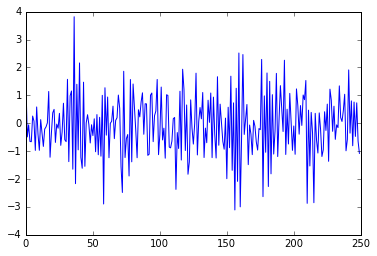
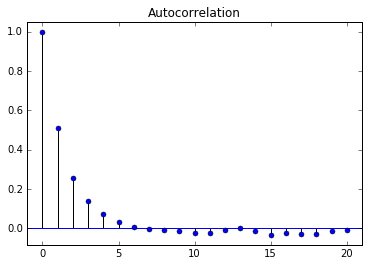
Comparison of AR(1) Autocorrelation Functions

$\large \phi=0.9$
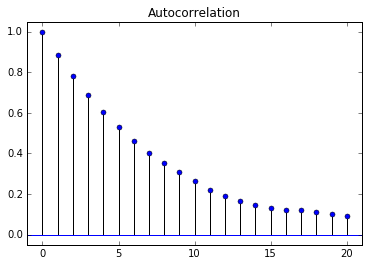
$\large \phi=0.5$

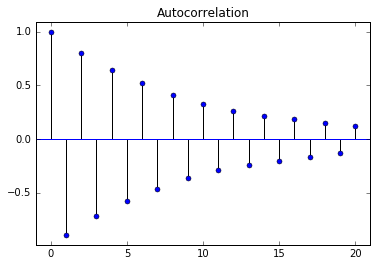
$\large \phi=-0.9$
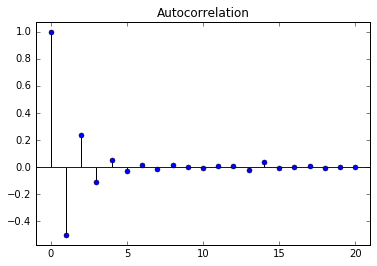
$\large \phi=-0.5$

Higher Order AR Models

AR(1)

$\large \quad \quad R_t = \mu + \phi_1 R_{t-1} + \epsilon_t$

AR(2)

$\large \quad \quad R_t = \mu + \phi_1 R_{t-1} + \phi_2 R_{t-2} + \epsilon_t$

AR(3)

$\large \quad \quad R_t = \mu + \phi_1 R_{t-1} + \phi_2 R_{t-2} + \phi_3 R_{t-3} + \epsilon_t$

...

Simulating an AR Process

from statsmodels.tsa.arima_process import ArmaProcess
ar = np.array([1, -0.9])
ma = np.array([1])
AR_object = ArmaProcess(ar, ma)
simulated_data = AR_object.generate_sample(nsample=1000)
plt.plot(simulated_data)

Let's practice!

Time Series Analysis in Python

Preparing Video For Download...