Volatility and extreme values

Quantitative Risk Management in Python

Jamsheed Shorish

Computational Economist

Chow test assumptions

  • Chow test: identify statistical significance of possible structural break
  • Requires: pre-specified point of structural break
  • Requires: linear relation (e.g. factor model) $$ \log(\text{Population}_t) = \alpha + \beta * \text{Year}_t + u_t $$

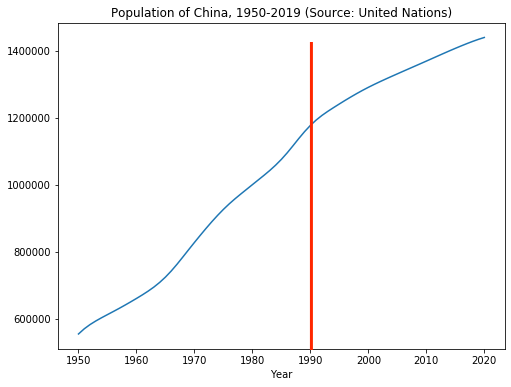
Image of china population growth with structural break point shown

Quantitative Risk Management in Python

Structural break indications

  • Visualization of trend may not indicate break point
  • Alternative: examine volatility rather than trend
    • Structural change often accompanied by greater uncertainty => volatility
    • Allows richer models to be considered (e.g. stochastic volatility models)

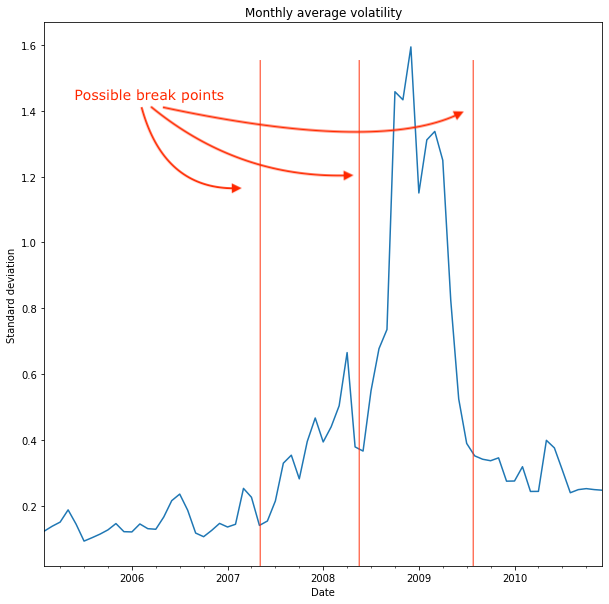
Image of monthly volatility with possible structural break points

Quantitative Risk Management in Python

Rolling window volatility

  • Rolling window: compute volatility over time and detect changes

  • Recall: 30-day rolling window

    • Create rolling window from ".rolling()" method
    • Compute the volatility of the rolling window (drop unavailable dates)
    • Compute summary statistic of interest, e.g. .mean(), .min(), etc.

     

rolling = portfolio_returns.rolling(30)

volatility = rolling.std().dropna()

vol_mean = volatility.resample("M").mean()
Quantitative Risk Management in Python

Rolling window volatility

  • Visualize resulting volatility (variance or standard deviation)
import matplotlib.pyplot as plt
vol_mean.plot(
  title="Monthly average volatility"
).set_ylabel("Standard deviation")
plt.show()

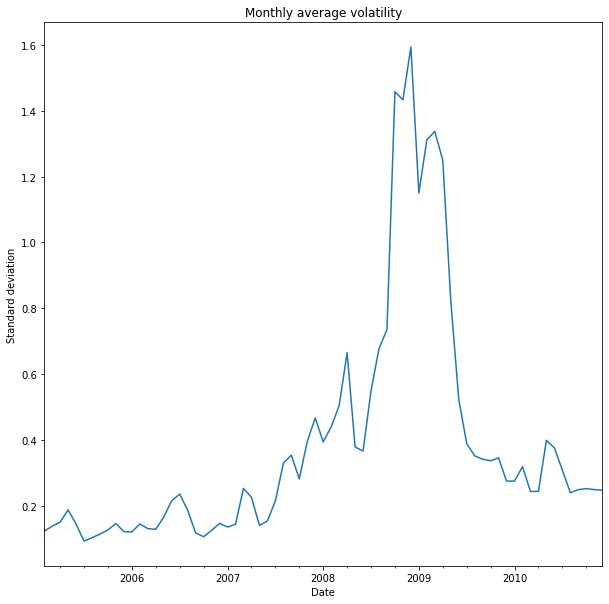
Image of monthly average volatility

Quantitative Risk Management in Python

Rolling window volatility

  • Visualize resulting volatility (variance or standard deviation)
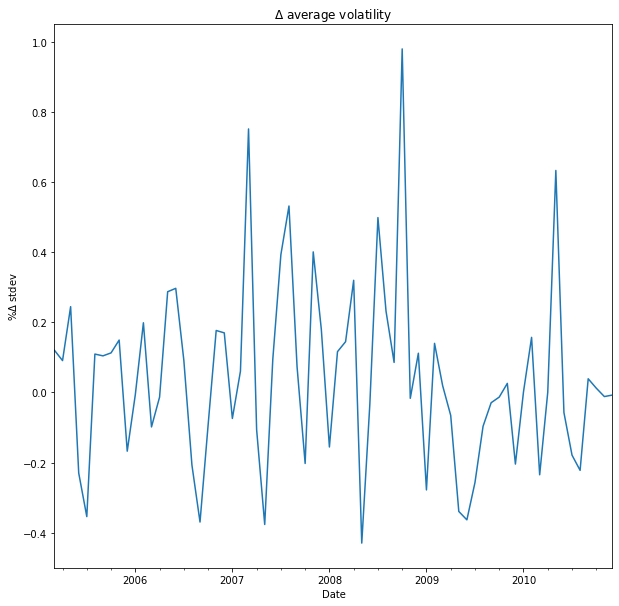
  • Large changes in volatility => possible structural break point(s)
  • Use proposed break points in linear model of volatility
    • Variant of Chow Test
  • Guidance for applying e.g. ARCH, stochastic volatility models
vol_mean.pct_change().plot(
  title="$\Delta$ average volatility"
).set_ylabel("% $\Delta$ stdev")
plt.show()

Image of percent change in monthly volatility

Quantitative Risk Management in Python

Extreme values

  • VaR, CVaR: maximum loss, expected shortfall at particular confidence level
  • Visualize changes in maximum loss by plotting VaR?
    • Useful for large datasets
    • Small datasets: not enough information
  • Alternative: find losses exceeding some threshold
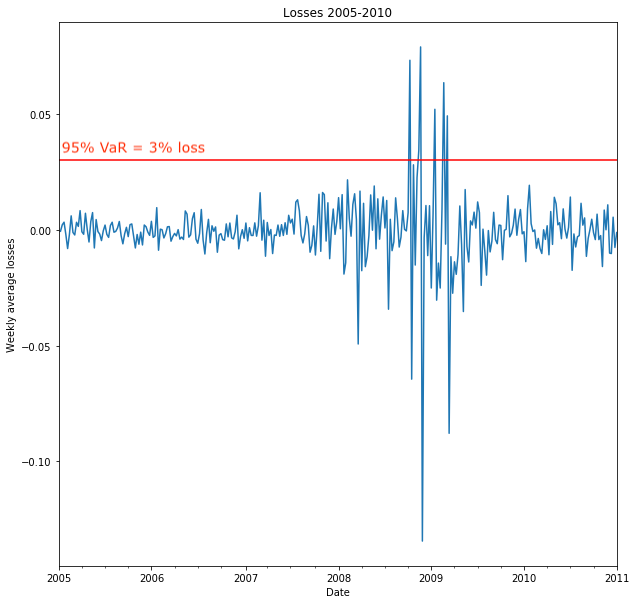
  • Example: $\text{VaR}_{95}$ is maximum loss 95% of the time
    • So 5% of the time, losses can be expected to exceed $\text{VaR}_{95}$
  • Backtesting: use previous data ex-post to see how risk estimate performs
    • Used extensively in enterprise risk management
Quantitative Risk Management in Python

Backtesting

  • Suppose $\text{VaR}_{95} = 0.03$
  • Losses exceeding 3% are then extreme values
  • Backtesting: around 5% (100% - 95%) of previous losses should exceed 3%
    • More than 5%: distribution with wider ("fatter") tails
    • Less than 5%: distribution with narrower tails
  • CVaR for backtesting: accounts for tail better than VaR

Image of losses and 95% VaR threshold

Quantitative Risk Management in Python

Let's practice!

Quantitative Risk Management in Python

Preparing Video For Download...