Kernel density estimation

Quantitative Risk Management in Python

Jamsheed Shorish

Computational Economist

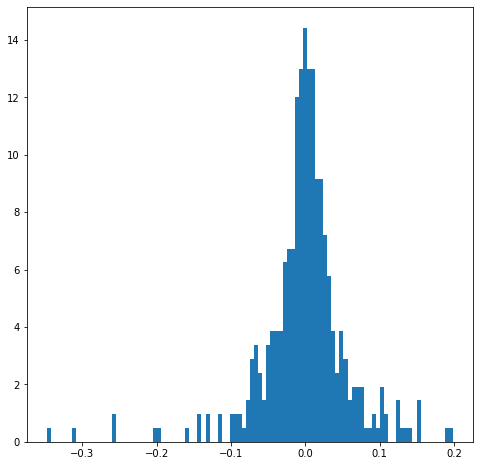
The histogram revisited

  • Risk factor distributions
    • Assumed (e.g. Normal, T, etc.)
    • Fitted (parametric estimation, Monte Carlo simulation)
    • Ignored (historical simulation)
  • Actual data: histogram
  • How to represent histogram by probability distribution?
    • Smooth data using filtering
    • Non-parametric estimation

histogram of losses

Quantitative Risk Management in Python

Data smoothing

  • Filter: smoothen out 'bumps' of histogram

histogram axes

Quantitative Risk Management in Python

Data smoothing

  • Filter: smoothen out 'bumps' of histogram
  • Observations accumulate in over time

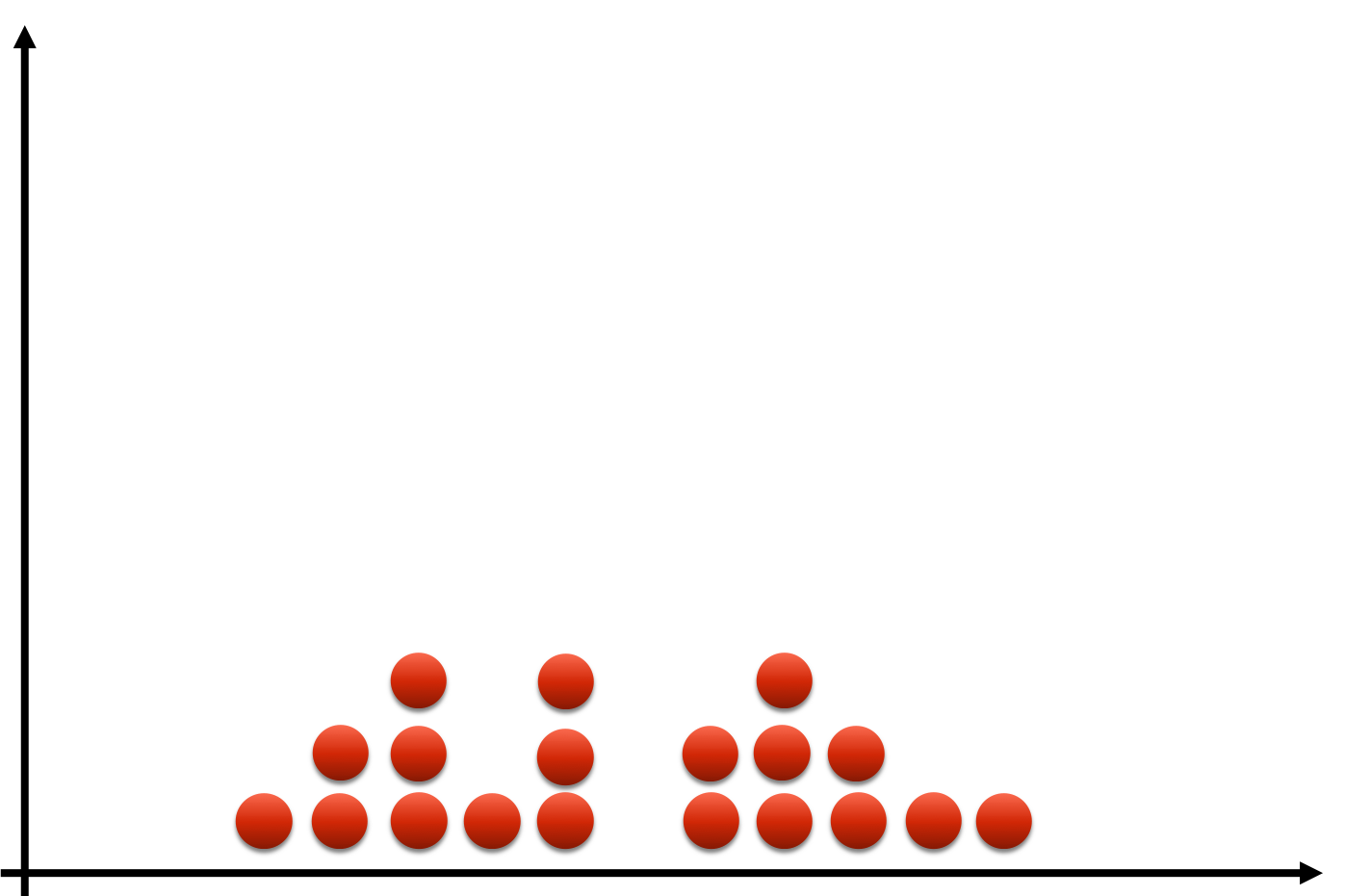
image of observations accumulating

Quantitative Risk Management in Python

Data smoothing

  • Filter: smoothen out 'bumps' of histogram
  • Observations accumulate in over time

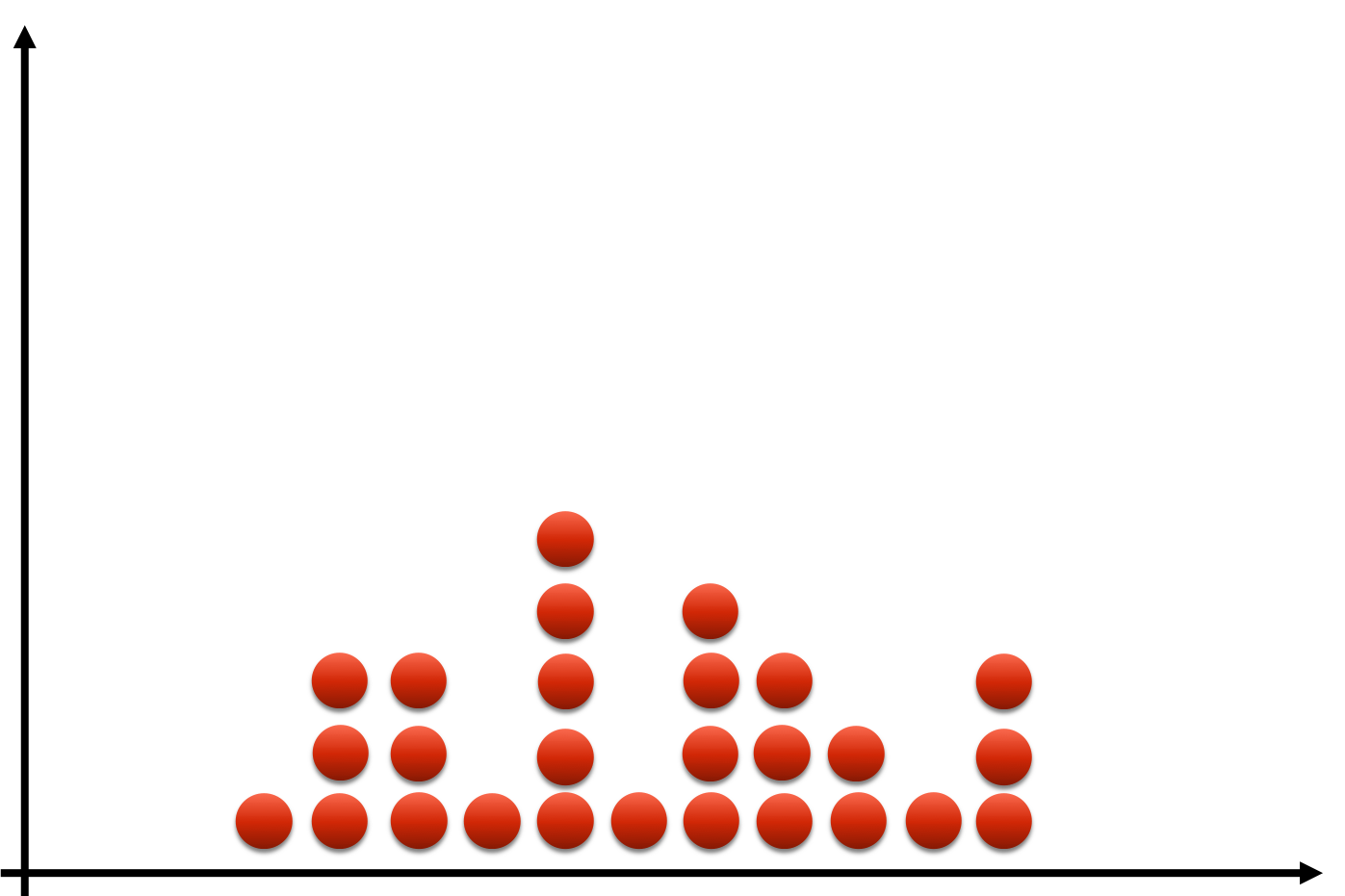
image of observations accumulating

Quantitative Risk Management in Python

Data smoothing

  • Filter: smoothen out 'bumps' of histogram
  • Observations accumulate in over time

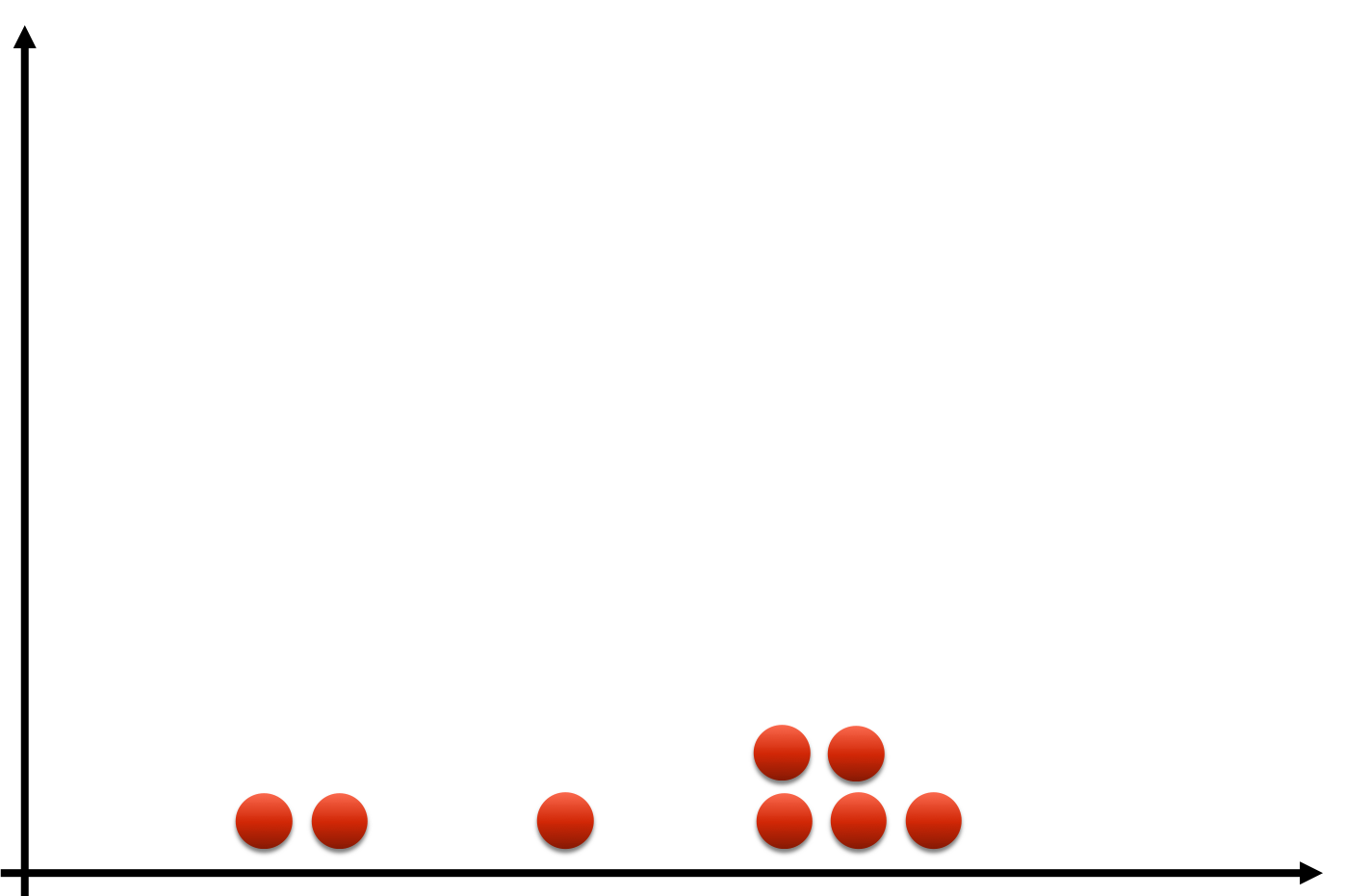
image of observations accumulating

Quantitative Risk Management in Python

Data smoothing

  • Filter: smoothen out 'bumps' of histogram
  • Observations accumulate in over time
  • Pick particular portfolio loss

losses and particular loss chosen with arrow

Quantitative Risk Management in Python

Data smoothing

  • Filter: smoothen out 'bumps' of histogram
  • Observations accumulate in over time
  • Pick particular portfolio loss
    • Examine nearby losses

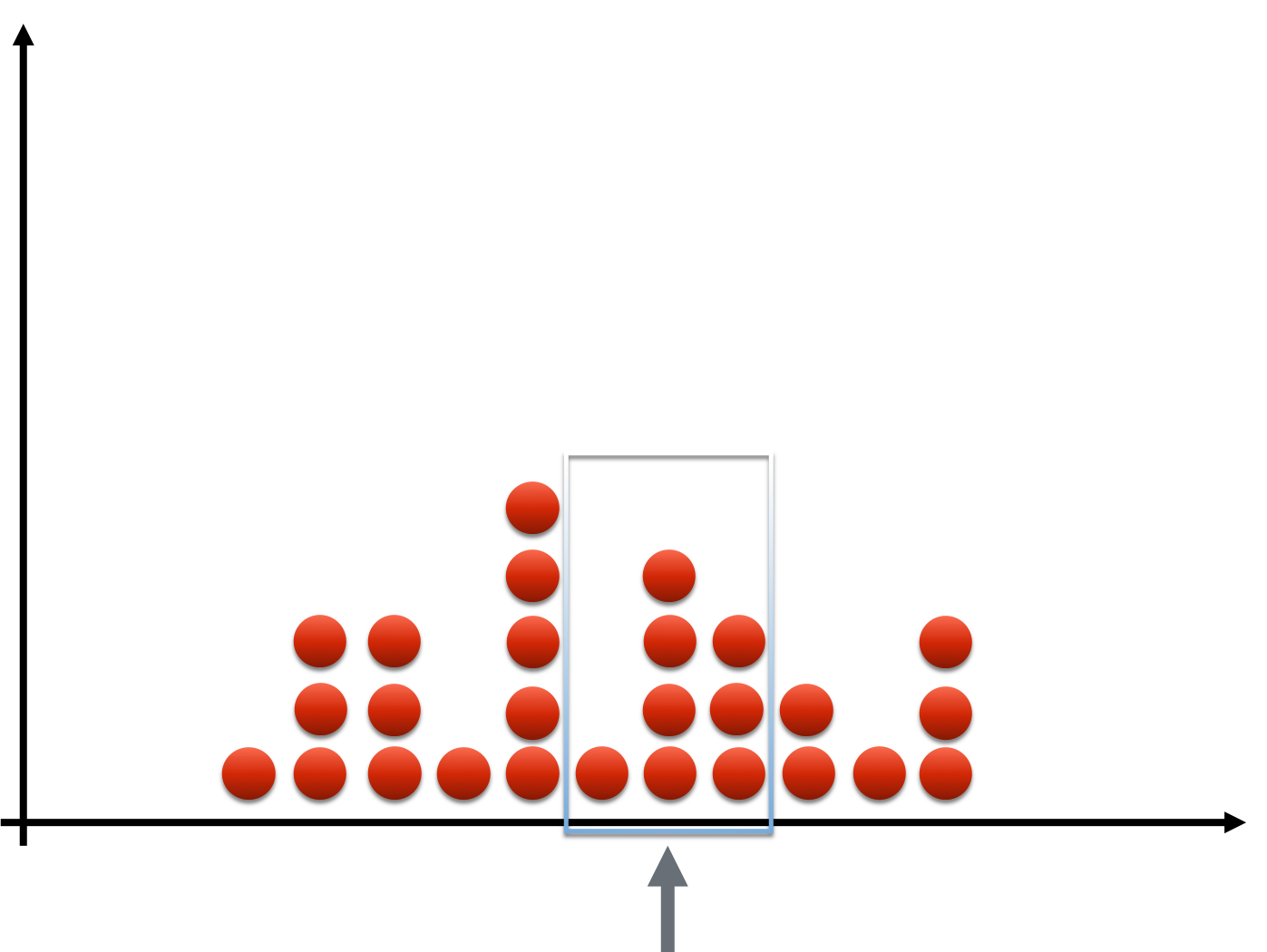
kernel window superimposed over observations

Quantitative Risk Management in Python

Data smoothing

  • Filter: smoothen out 'bumps' of histogram
  • Observations accumulate in over time
  • Pick particular portfolio loss
    • Examine nearby losses
    • Form "weighted average" of losses
  • Kernel: filter choice; determines "window"

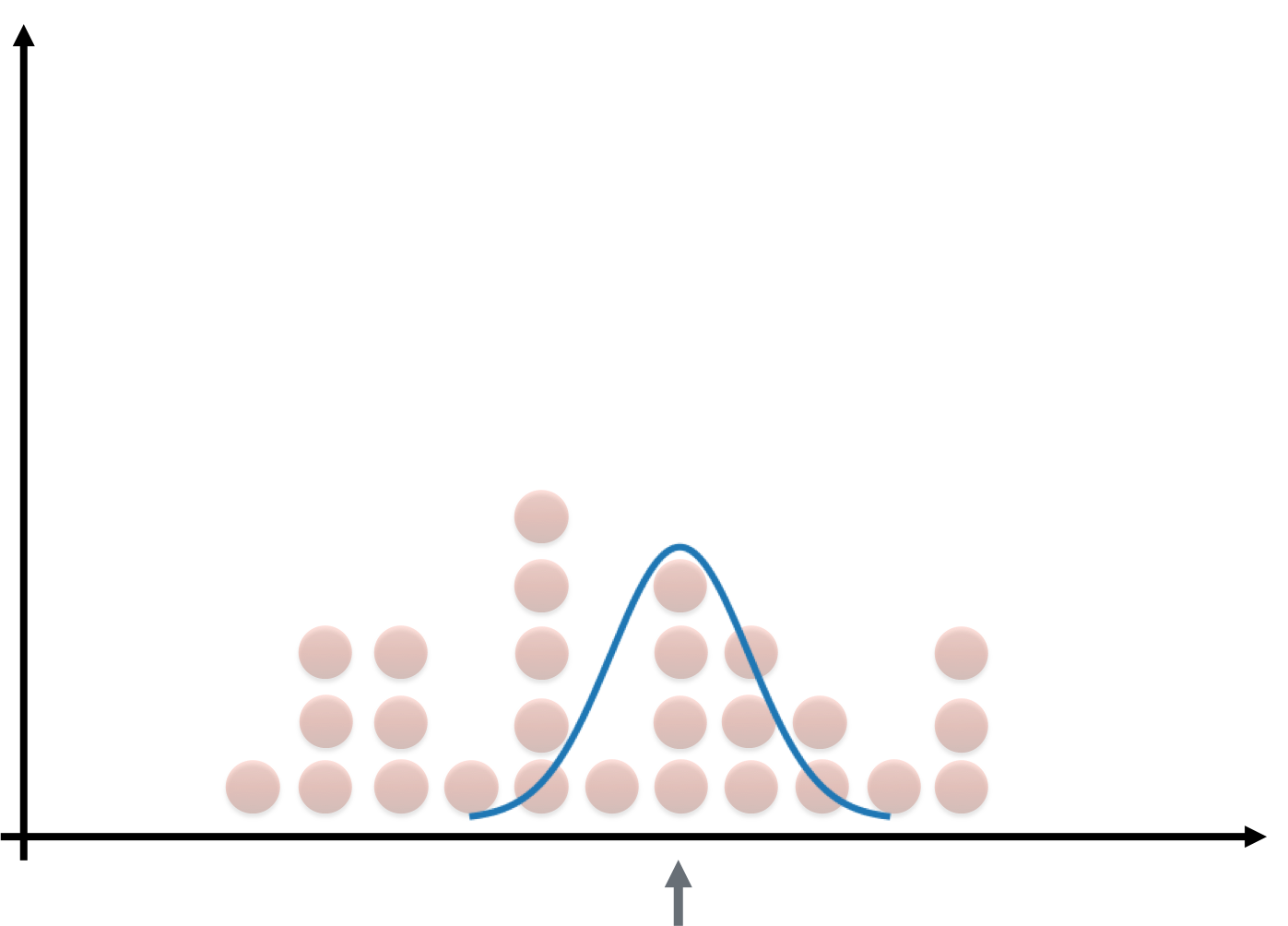
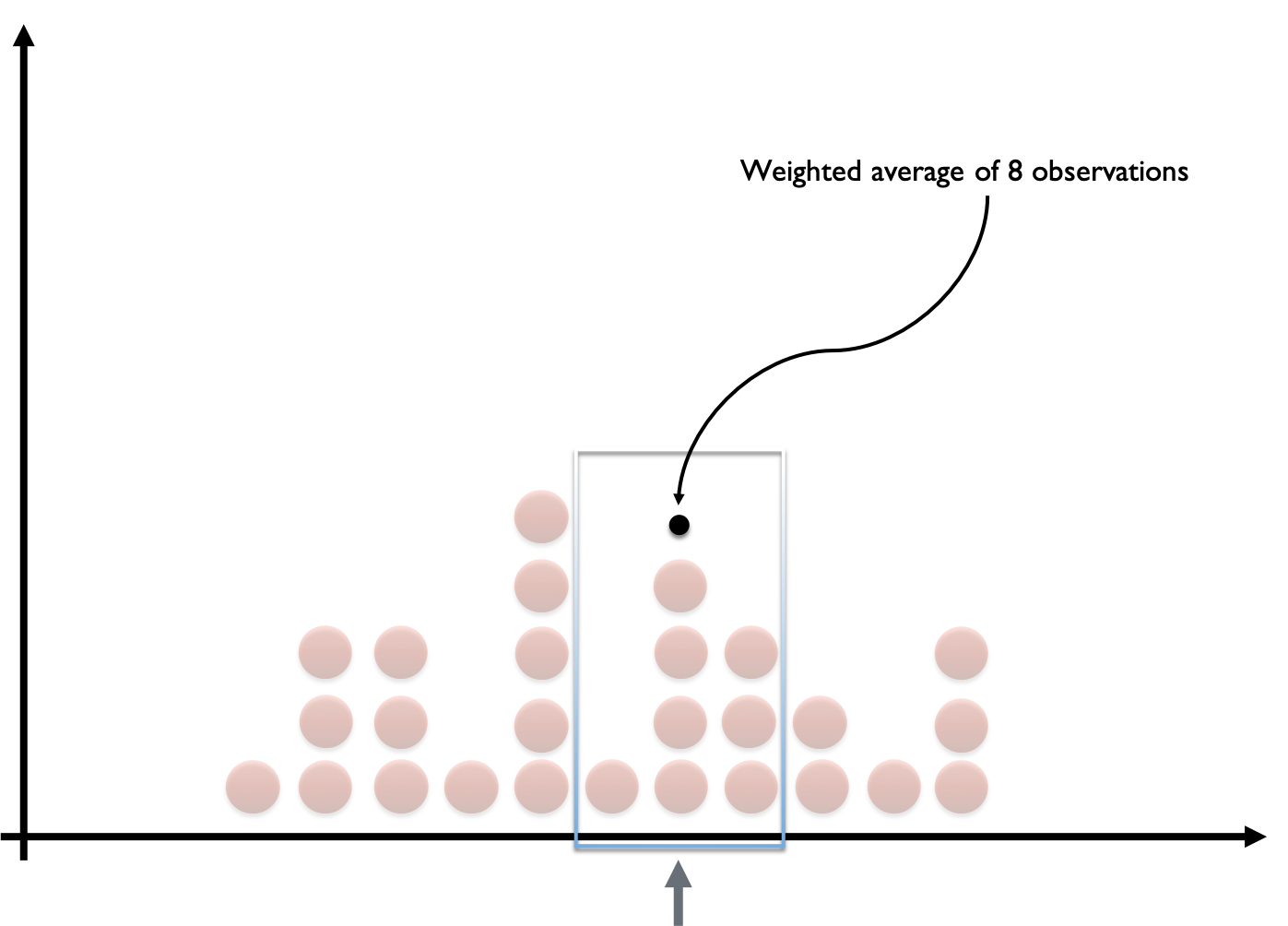
weighted average from kernel displayed on image

Quantitative Risk Management in Python

Data smoothing

  • Filter: smoothen out 'bumps' of histogram
  • Observations accumulate in over time
  • Pick particular portfolio loss
    • Examine nearby losses
    • Form "weighted average" of losses
  • Kernel: filter choice; determines "window"
    • Move window to another loss

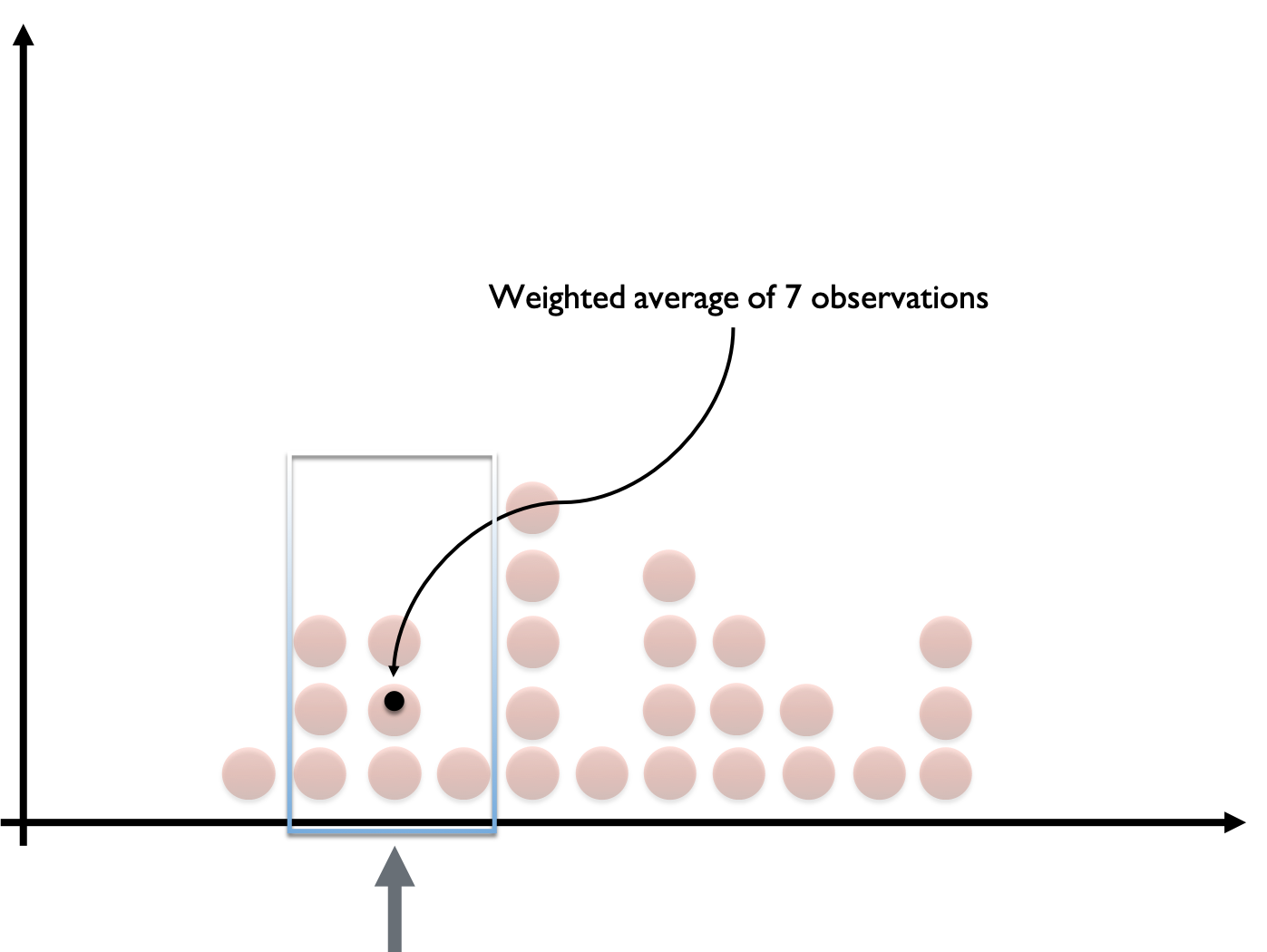
image of second kernel location

Quantitative Risk Management in Python

Data smoothing

  • Filter: smoothen out 'bumps' of histogram
  • Observations accumulate in over time
  • Pick particular portfolio loss
    • Examine nearby losses
    • Form "weighted average" of losses
  • Kernel: filter choice; determines "window"
    • Move window to another loss
  • Kernel density estimate: probability density

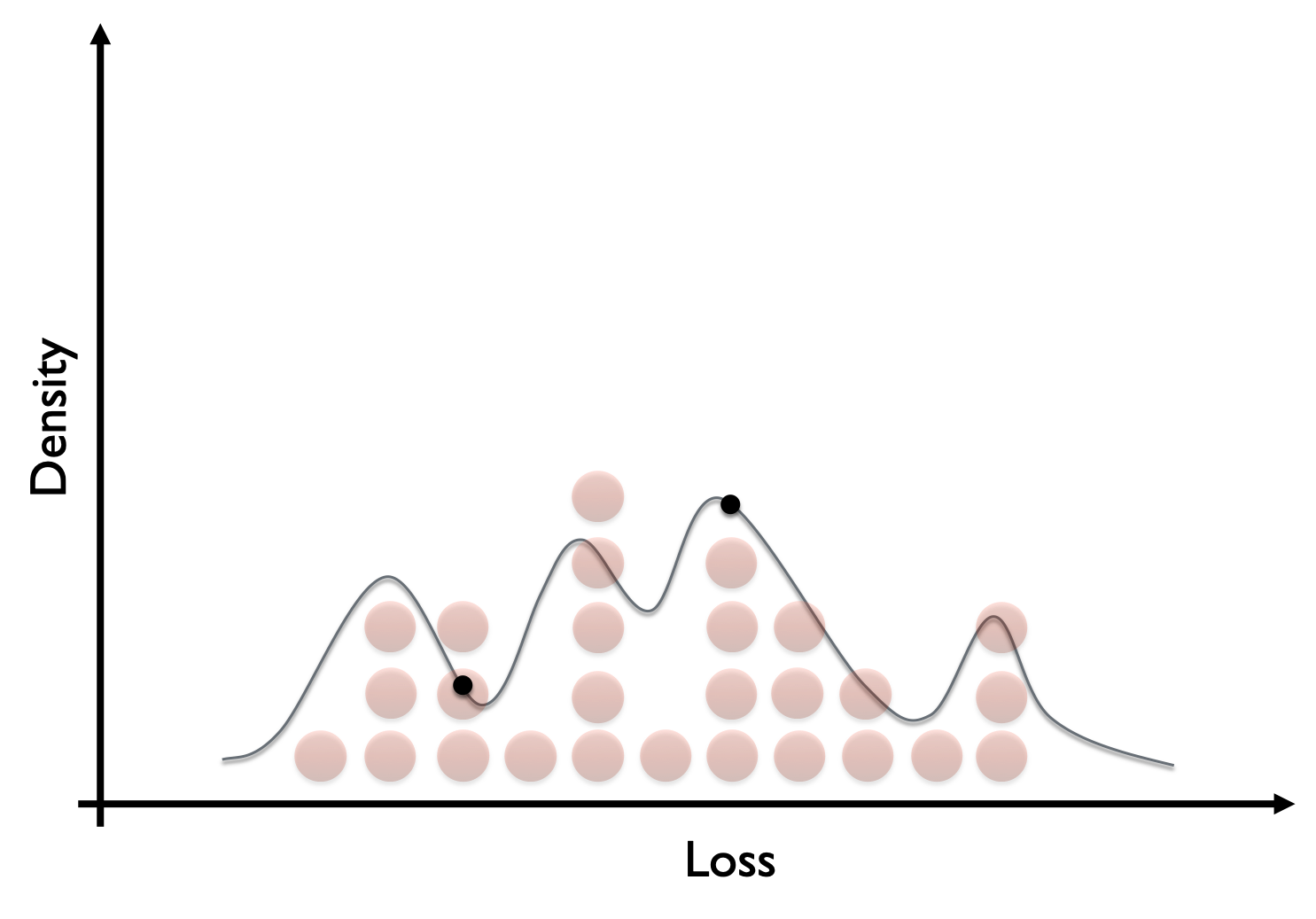
image of kernel density estimate

Quantitative Risk Management in Python

The Gaussian kernel

  • Continuous kernel
  • Weights all observations by distance from center
  • Generally: many different kernels are available
    • Used in time series analysis
    • Used in signal processing

image of Gaussian kernel

Quantitative Risk Management in Python

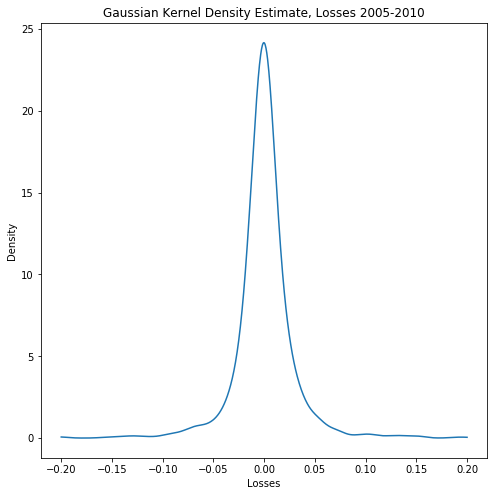
KDE in Python

from scipy.stats import gaussian_kde

kde = guassian_kde(losses)

loss_range = np.linspace(np.min(losses),
                np.max(losses),
                1000)

plt.plot(loss_range, kde.pdf(loss_range))
  • Visualization: probability density function from KDE fit

gaussian kde estimate plot

Quantitative Risk Management in Python

Finding VaR using KDE

  • VaR: use gaussian_kde .resample() method
  • Find quantile of resulting sample
  • CVaR: expected value as previously encountered, but
    • gaussian_kde has no .expect() method => compute integral manually
    • special .expect() method written for exercise
sample = kde.resample(size = 1000)

VaR_99 = np.quantile(sample, 0.99)

print("VaR_99 from KDE: ", VaR_99)

VaR_99 from KDE: 0.08796423698448601
Quantitative Risk Management in Python

Let's practice!

Quantitative Risk Management in Python

Preparing Video For Download...