Modern portfolio theory
Quantitative Risk Management in Python

Jamsheed Shorish
Computational Economist
The risk-return trade-off
- Risk factors: sources of uncertainty affecting return
- Intuitively: greater uncertainty (more risk) compensated by greater return
- Cannot guarantee return: need some measure of expected return
- average (mean) historical return: proxy for expected future return
Investor risk appetite
- Investor survey: minimum return required for given level of risk?
- Survey response creates (risk, return) risk profile "data point"
- Vary risk level => set of (risk, return) points
- Investor risk appetite: defines one quantified relationship between risk and return
Choosing portfolio weights
- Vary portfolio weights of given portfolio => creates set of (risk, return) pairs
- Changing weights = beginning risk management!
- Goal: change weights to maximize expected return, given risk level
- Equivalently: minimize risk, given expected return level
- Changing weights = adjusting investor's risk exposure
Modern portfolio theory
- Efficient portfolio: portfolio with weights generating highest expected return for given level of risk
- Modern Portfolio Theory (MPT), 1952
- H. M. Markowitz (Nobel Laureate 1990)
- Efficient portfolio weight vector $w^\star$ solves:
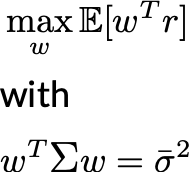
The efficient frontier
- Compute many efficient portfolios for different levels of risk
- Efficient frontier: locus of (risk, return) pairs created by efficient portfolios
PyPortfolioOptlibrary: optimized tools for MPTEfficientFrontierclass: generates one optimal portfolio at a time- Constrained Line Algorithm (
CLA) class: generates the entire efficient frontier- Requires covariance matrix of returns
- Requires proxy for expected future returns: mean historical returns
Investment bank portfolio 2005 - 2010
- Expected returns: historical data
- Covariance matrix:
Covariance Shrinkageimproves efficiency of estimate - Constrained Line Algorithm object
CLA - Minimum variance portfolio:
cla.min_volatility() - Efficient frontier:
cla.efficient_frontier()
expected_returns = mean_historical_return(prices)efficient_cov = CovarianceShrinkage(prices).ledoit_wolf()cla = CLA(expected_returns, efficient_cov)minimum_variance = cla.min_volatility()(ret, vol, weights) = cla.efficient_frontier()
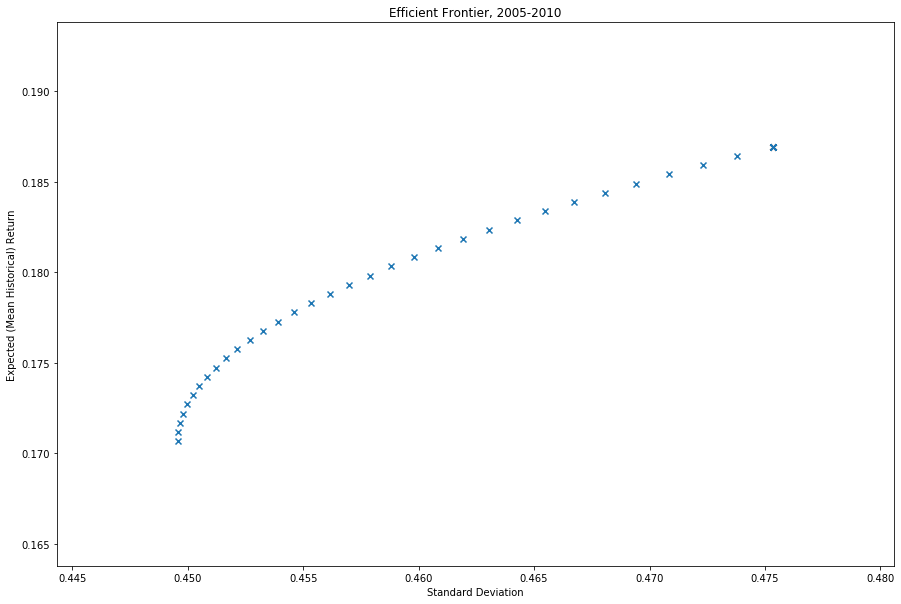
Visualizing the efficient frontier
- Scatter plot of (vol, ret) pairs
Visualizing the efficient frontier
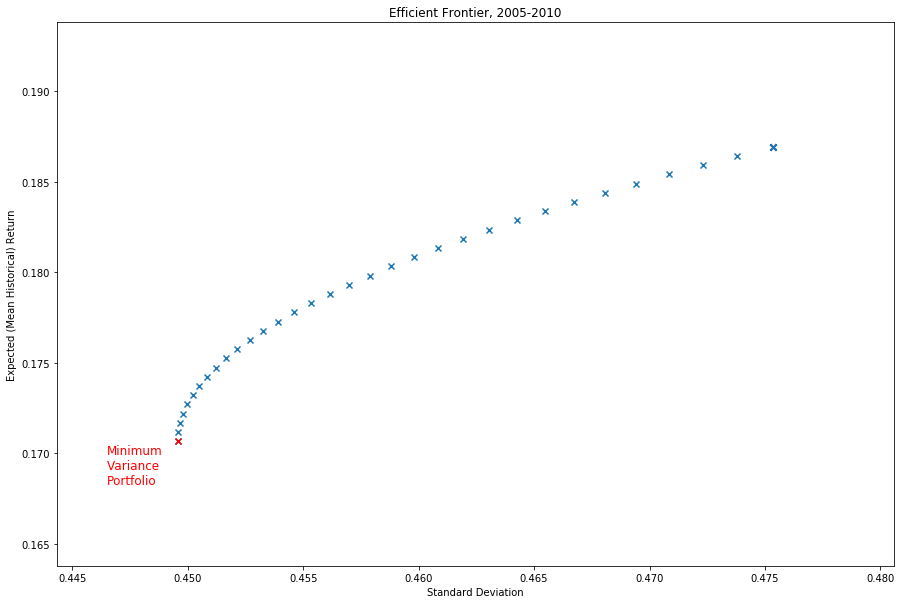
- Scatter plot of (vol, ret) pairs
- Minimum variance portfolio: smallest volatility of all possible efficient portfolios
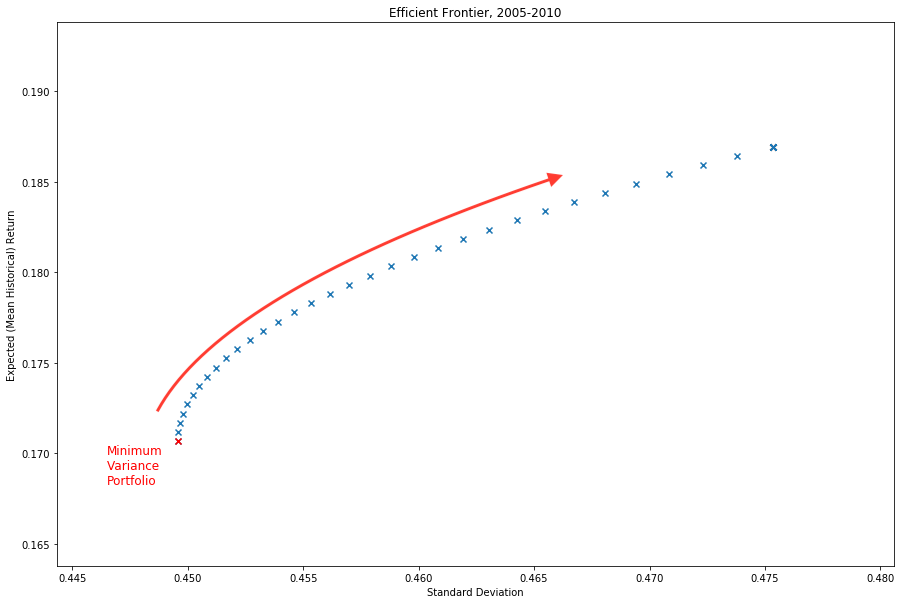
Visualizing the efficient frontier
- Scatter plot of (vol, ret) pairs
- Minimum variance portfolio: smallest volatility of all possible efficient portfolios
- Increasing risk appetite: move along the frontier
Let's practice!
Quantitative Risk Management in Python

