Choosing probability distributions
Monte Carlo Simulations in Python

Izzy Weber
Curriculum Manager, DataCamp
Maximum Likelihood Estimation (MLE)
- Used to select a probability distribution by measuring fit
- Distribution yielding highest likelihood given the data is considered optimal
- SciPy's
.nnlf()used to calculate the negative likelihood function - The lower the MLE value calculated using
.nnlf(), the better the fit
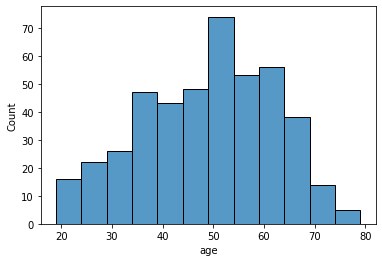
Picking a distribution for the age variable
sns.histplot(dia["age"])
Candidate distributions
distributions = [st.laplace, st.norm, st.expon]
Choosing between candidate distributions
mles = []for distribution in distributions: pars = distribution.fit(dia["age"])mle = distribution.nnlf(pars, dia["age"])mles.append(mle)print(mles)
[1797.8467779878652, 1764.0693689033028, 1938.171599681118]
Choosing between candidate distributions
for var in ["age", "bmi", "bp", "tc", "ldl", "hdl", "tch", "ltg", "glu"]:distributions = [st.laplace, st.norm, st.expon] mles = []for distribution in distributions: pars = distribution.fit(dia[var]) mle = distribution.nnlf(pars, dia[var]) mles.append(mle)best_fit = sorted(zip(distributions, mles), key=lambda d: d[1])[0] print(f"Best fit reached using {best_fit[0].name}, \ MLE value: {best_fit[1]}, for variable {var}")
Results of the evaluation
Best fit reached using norm, MLE value: 1764.0693689033028, for variable age
Best fit reached using norm, MLE value: 1283.356127017369, for variable bmi
Best fit reached using norm, MLE value: 1787.7746251622739, for variable bp
Best fit reached using norm, MLE value: 2193.1564373753627, for variable to
Best fit reached using norm, MLE value: 2136.0440476305284, for variable ldl
Best fit reached using norm, MLE value: 1758.1350738323013, for variable hdl
Best fit reached using norm, MLE value: 739.3762494786798, for variable tch
Best fit reached using norm, MLE value: 339.6620870566908, for variable ltg
Best fit reached using norm, MLE value: 1706.0467588930867, for variable glu
Let's practice!
Monte Carlo Simulations in Python

