Generating continuous random variables

Monte Carlo Simulations in Python

Izzy Weber

Curriculum Manager, DataCamp

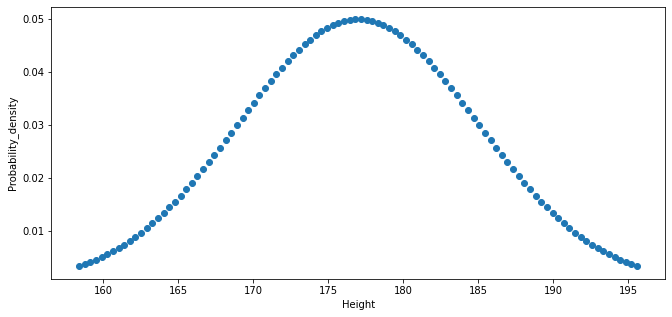
Normal distribution

Bell-shaped and centered at the mean (or loc); width defined by standard deviation (or scale)

The heights of American adult males are normally distributed: Theoretical probability density function of normal distribution

Monte Carlo Simulations in Python

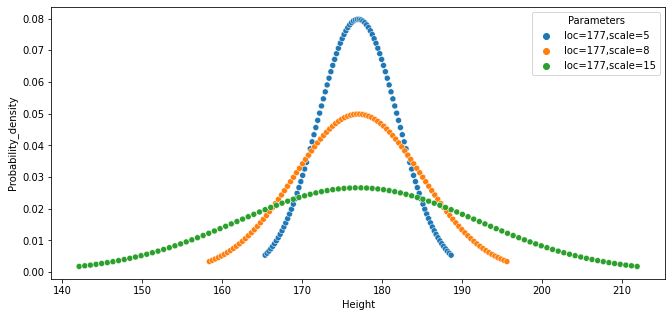
Changing the scale (standard deviation)

Theoretical probability density function of normal distribution with different standard deviations

Monte Carlo Simulations in Python

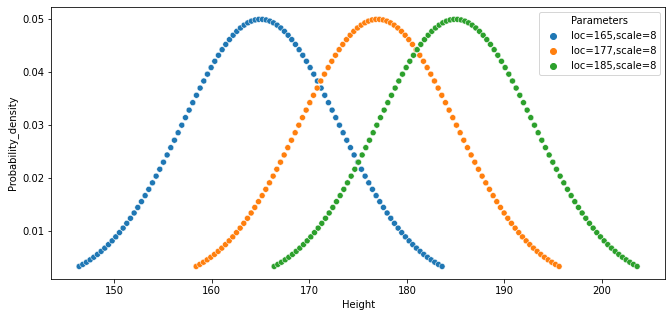
Changing the loc (mean)

Theoretical probability density function of normal distribution with different means

Monte Carlo Simulations in Python

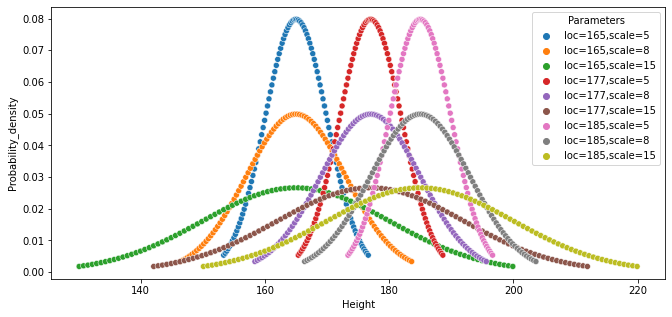
Changing both scale and loc

Theoretical probability density function of normal distribution with different standard deviations and means

Monte Carlo Simulations in Python

Sampling from normal distributions

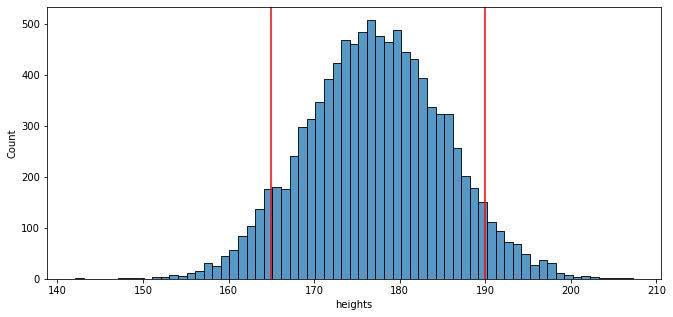
  • Normally distributed US adult male heights; mean = 177 cm; standard deviation = 8 cm

  • What's the percentage of people with a height either above 190 or below 165 cm? 

heights = st.norm.rvs(loc=177, scale=8, size=10000)

qualified = (heights < 165) | (heights > 190)

print(np.sum(qualified) * 100/10000)

12.28
Monte Carlo Simulations in Python

Plotting simulation results

heights_dict = {"heights":heights}
sns.histplot(x="heights", data=heights_dict)
plt.axvline(x=165, color="red")
plt.axvline(x=190, color="red")

Histogram of samples taken from normal distribution

Monte Carlo Simulations in Python

More continuous probability distributions

  • Continuous Uniform distribution (st.uniform)
    • The continuous analog of the discrete uniform distribution
  • Exponential distribution (st.expon)
    • The continuous analog of the geometric distribution
1 https://docs.scipy.org/doc/scipy/tutorial/stats/continuous.html
Monte Carlo Simulations in Python

Let's practice!

Monte Carlo Simulations in Python

Preparing Video For Download...