Grundlagen der linearen Regression

Überwachtes Lernen mit scikit-learn

George Boorman

Core Curriculum Manager, DataCamp

Grundprinzip der Regression

  • $y = ax + b$

    • Einfache lineare Regression verwendet ein Merkmal

      • $y$ = Zielvariable

      • $x$ = einzelnes Merkmal

      • $a$, $b$ = Parameter/Koeffizienten des Modells (Steigung und Achsenabschnitt)

  • Wie wählen wir $a$ und $b$?

    • Definition einer Fehlerfunktion für eine Gerade

    • Auswahl der Geraden, die das Minimum der Fehlerfunktion liefert

  • Fehlerfunktion = Verlustfunktion = Kostenfunktion

Überwachtes Lernen mit scikit-learn

Verlustfunktion

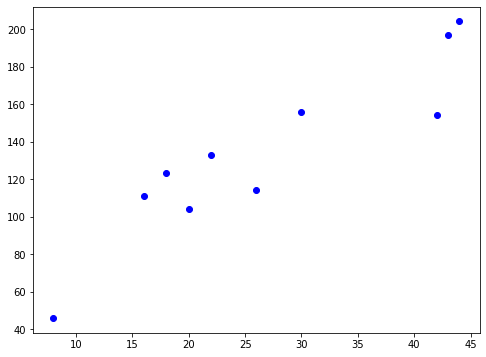
Streudiagramm

Überwachtes Lernen mit scikit-learn

Verlustfunktion

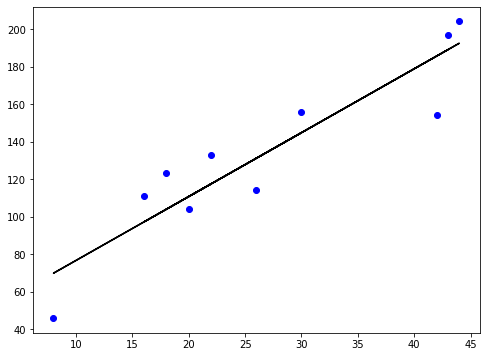
Regressionsgerade, die von links unten nach rechts oben und mitten durch die Datenpunkte verläuft

Überwachtes Lernen mit scikit-learn

Verlustfunktion

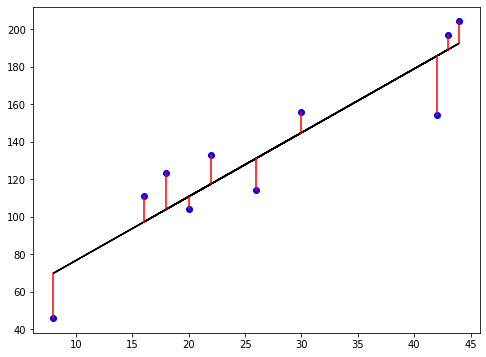
Rote Linien zeigen den vertikalen Abstand der Datenpunkte zur Regressionsgeraden

Überwachtes Lernen mit scikit-learn

Verlustfunktion

Rote Linien stellen die Residuen dar

Überwachtes Lernen mit scikit-learn

Verlustfunktion

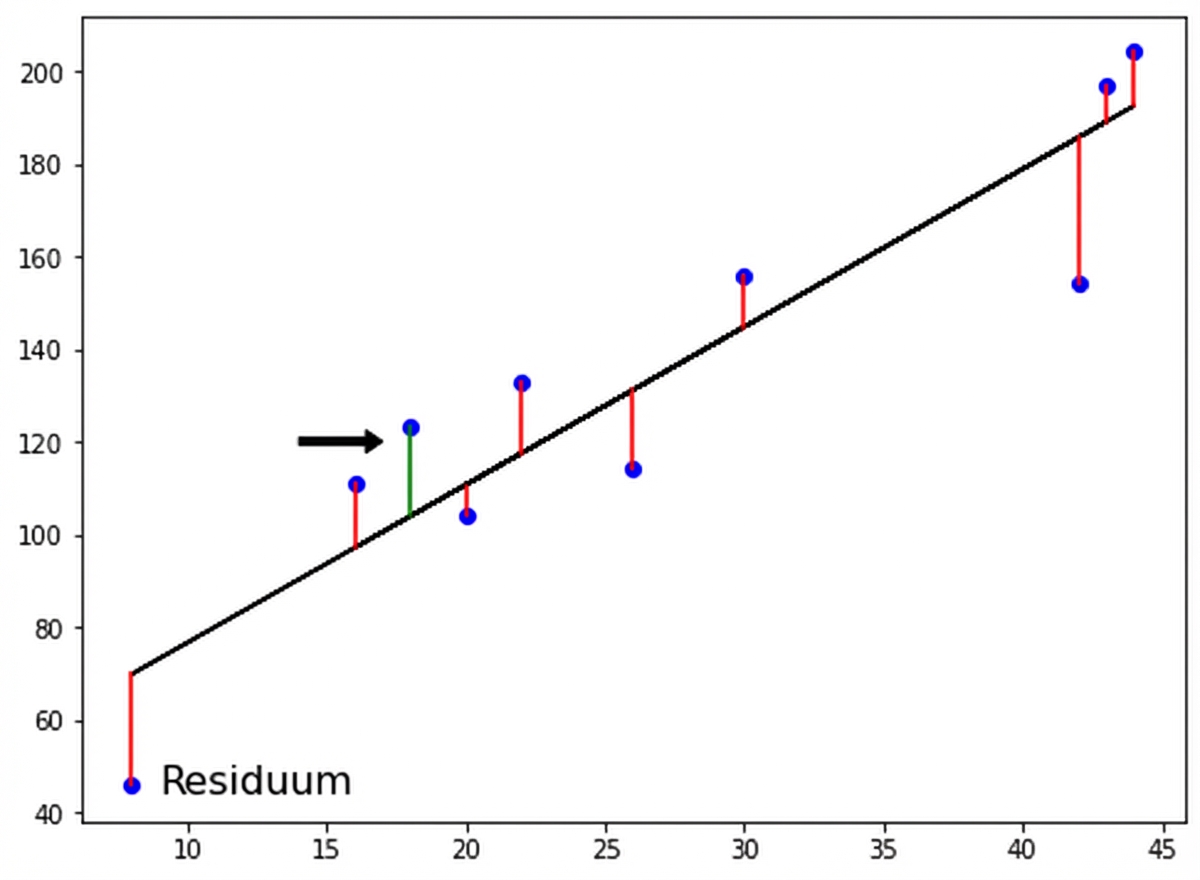
Pfeil zeigt auf ein positives Residuum; das heißt, der Datenpunkt liegt oberhalb der Regressionsgeraden

Überwachtes Lernen mit scikit-learn

Methode der kleinsten Quadrate

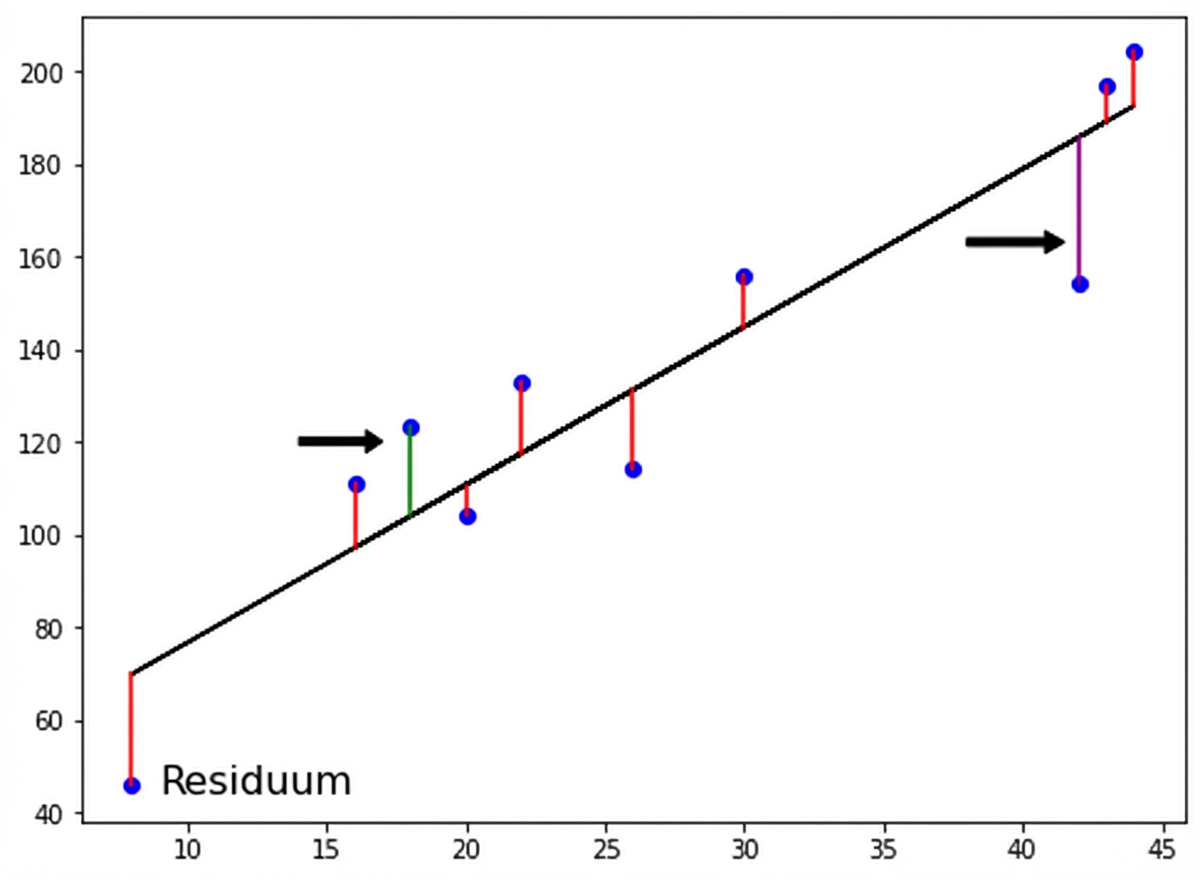
Zweiter Pfeil zeigt auf ein negatives Residuum; das heißt, der Datenpunkt liegt unterhalb der Regressionsgeraden

$RSS = $ $\displaystyle\sum_{i=1}^{n}(y_i-\hat{y_i})^2$

Methode der kleinsten Quadrate (OLS): RSS minimieren

Überwachtes Lernen mit scikit-learn

Lineare Regression mit mehr Dimensionen

$$ y = a_{1}x_{1} + a_{2}x_{2} + b$$

  • Anpassung eines Modells für die lineare Regression:
    • Drei Variablen sind hier anzugeben: $ a_1,\ a_2,\ b $
  • Mehr Dimensionen:
    • Auch bekannt als multiple Regression
    • Koeffizient für jedes Merkmal sowie die Variable $b$ sind anzugeben

$$ y = a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3} +... + a_{n}x_{n}+ b$$

  • scikit-learn arbeitet auf dieselbe Weise:
    • Zwei Arrays sind zu übergeben: Merkmale und Zielvariable
Überwachtes Lernen mit scikit-learn

Lineare Regression mithilfe aller Merkmale

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
                                                    random_state=42)

reg_all = LinearRegression()

reg_all.fit(X_train, y_train)

y_pred = reg_all.predict(X_test)
Überwachtes Lernen mit scikit-learn

Bestimmtheitsmaß ($R^2$)

  • $R^2$: gibt an, welcher Anteil der Varianz in den Zielwerten durch die Merkmale erklärt wird

    • Wertebereich von 0 bis 1

  • Hoher Wert für $R^2$:

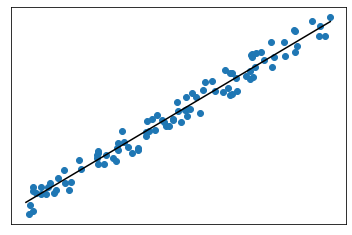
Regressionsgerade im Winkel von 45 Grad, die von links unten nach rechts oben verläuft und nahe an allen Datenpunkten liegt

 

 

  • Niedriger Wert für $R^2$:

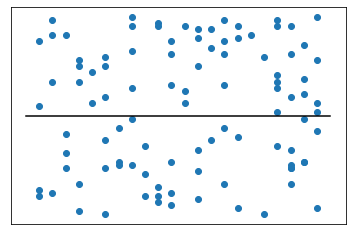
Waagerecht verlaufende Regressionsgerade, bei der die Datenpunkte verteilt und teils weit von der Geraden entfernt liegen

Überwachtes Lernen mit scikit-learn

$R^2$ in scikit-learn

reg_all.score(X_test, y_test)

0.356302876407827
Überwachtes Lernen mit scikit-learn

MSE und RMSE

$MSE = $ $\displaystyle\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y_i})^2$

  • $MSE$ (mittlerer quadratischer Fehler) wird in Einheit der Zielvariablen zum Quadrat gemessen

 

$RMSE = $ $\sqrt{MSE}$

  • $RMSE$ (Wurzel des mittleren quadratischen Fehlers) wird in derselben Einheit der Zielvariablen gemessen
Überwachtes Lernen mit scikit-learn

RMSE in scikit-learn

from sklearn.metrics import root_mean_squared_error


root_mean_squared_error(y_test, y_pred)

24.028109426907236
Überwachtes Lernen mit scikit-learn

Lass uns üben!

Überwachtes Lernen mit scikit-learn

Preparing Video For Download...