Aktivierungsfunktionen entdecken
Einführung in Deep Learning mit PyTorch

Jasmin Ludolf
Senior Data Science Content Developer, DataCamp
Aktivierungsfunktionen
$$
- Aktivierungsfunktionen fügen dem Netz Nichtlinearität hinzu
- Sigmoid für binäre Klassifizierung
- Softmax für Mehrklassen-Klassifizierung
- Ein Netz kann komplexere Beziehungen mit Nicht-Linearität erlernen
- "Voraktivierungs"-Ausgang, der an die Aktivierungsfunktion übergeben wird
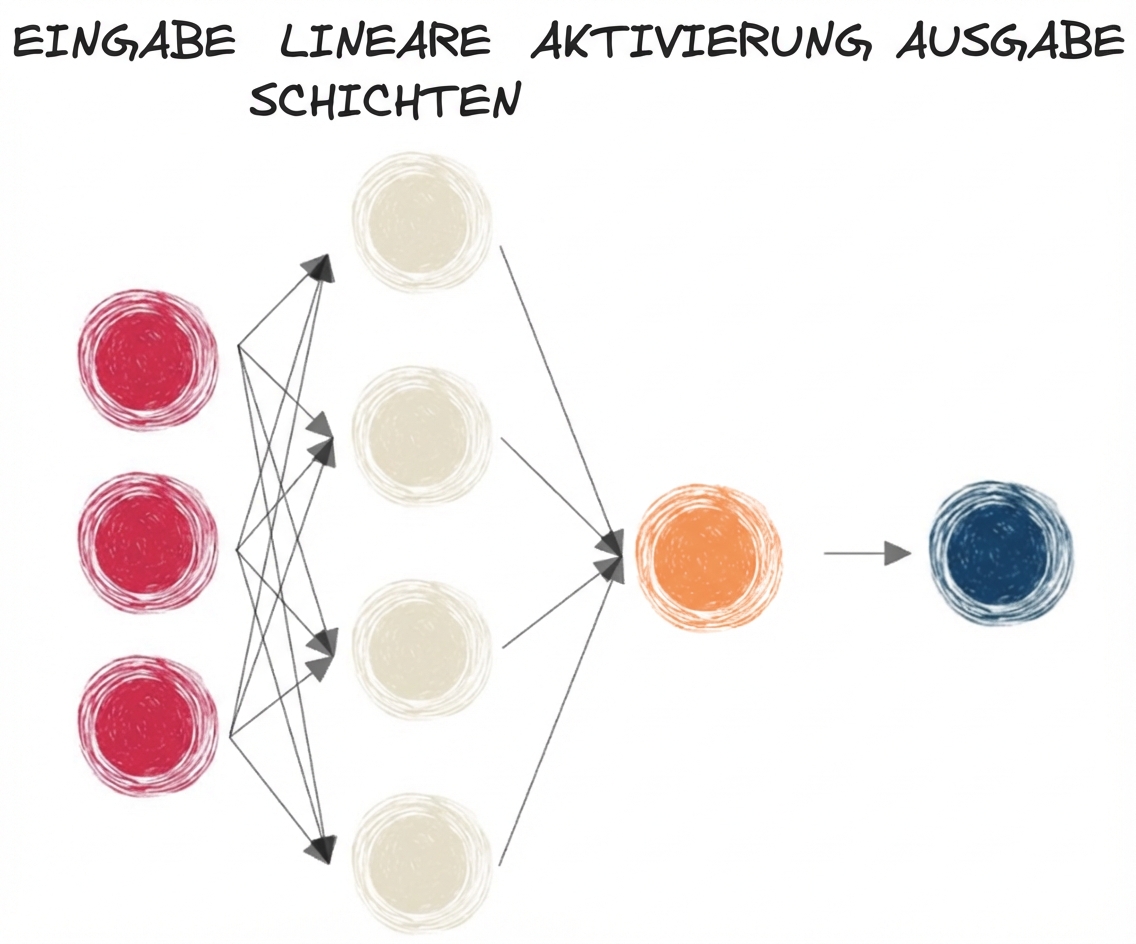
Die Sigmoid-Funktion
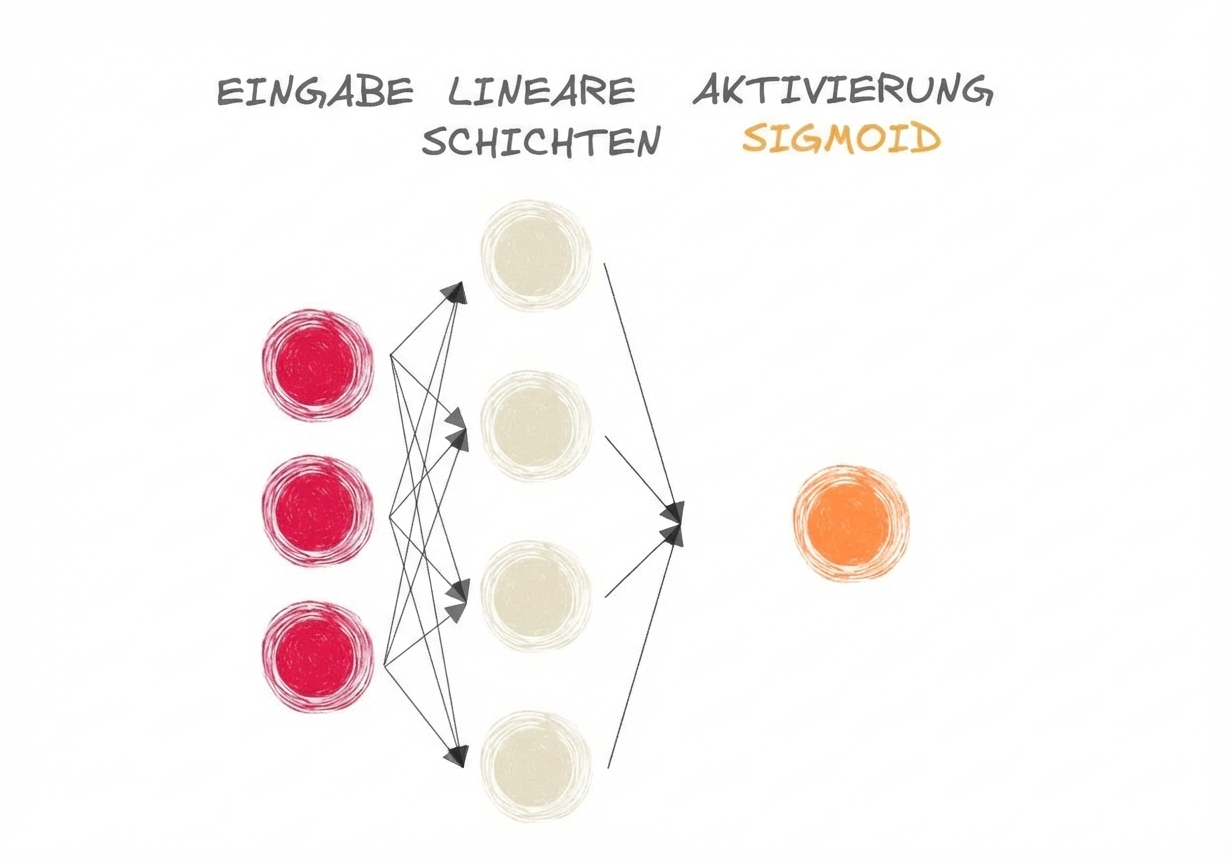
- Säugetier oder nicht?

Die Sigmoid-Funktion
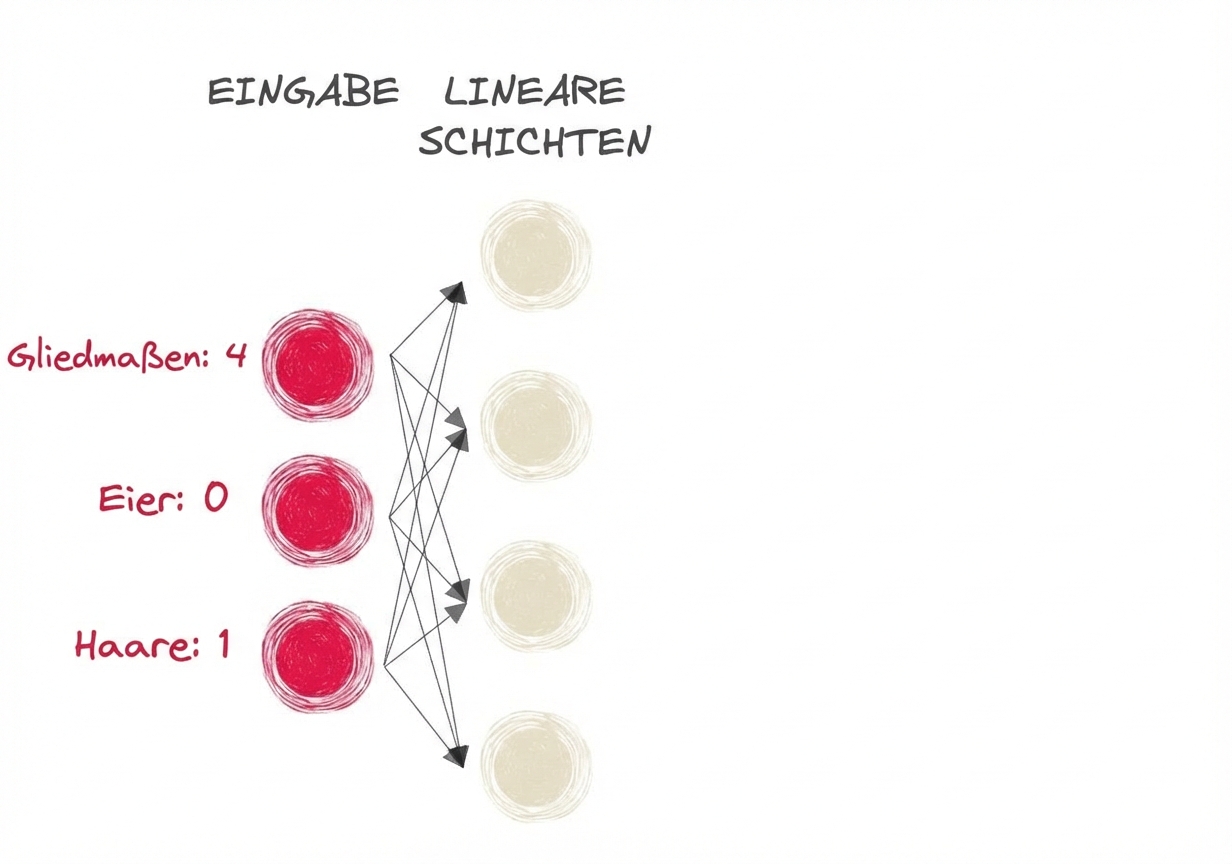
- Säugetier oder nicht?

- Eingabe:
- Gliedmaßen: 4
- Eier: 0
- Haare: 1
Die Sigmoid-Funktion
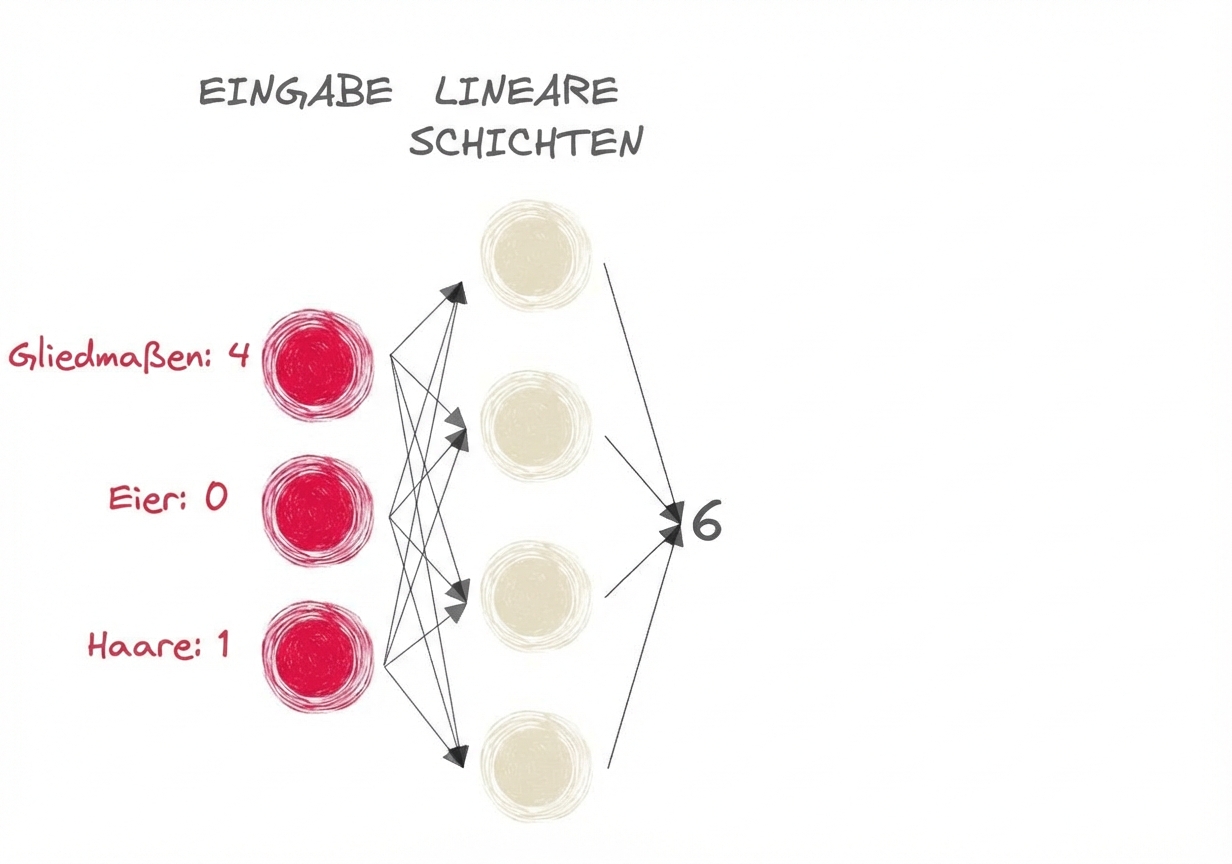
- Säugetier oder nicht?

- Die Ausgabe an die linearen Schichten ist 6
Die Sigmoid-Funktion
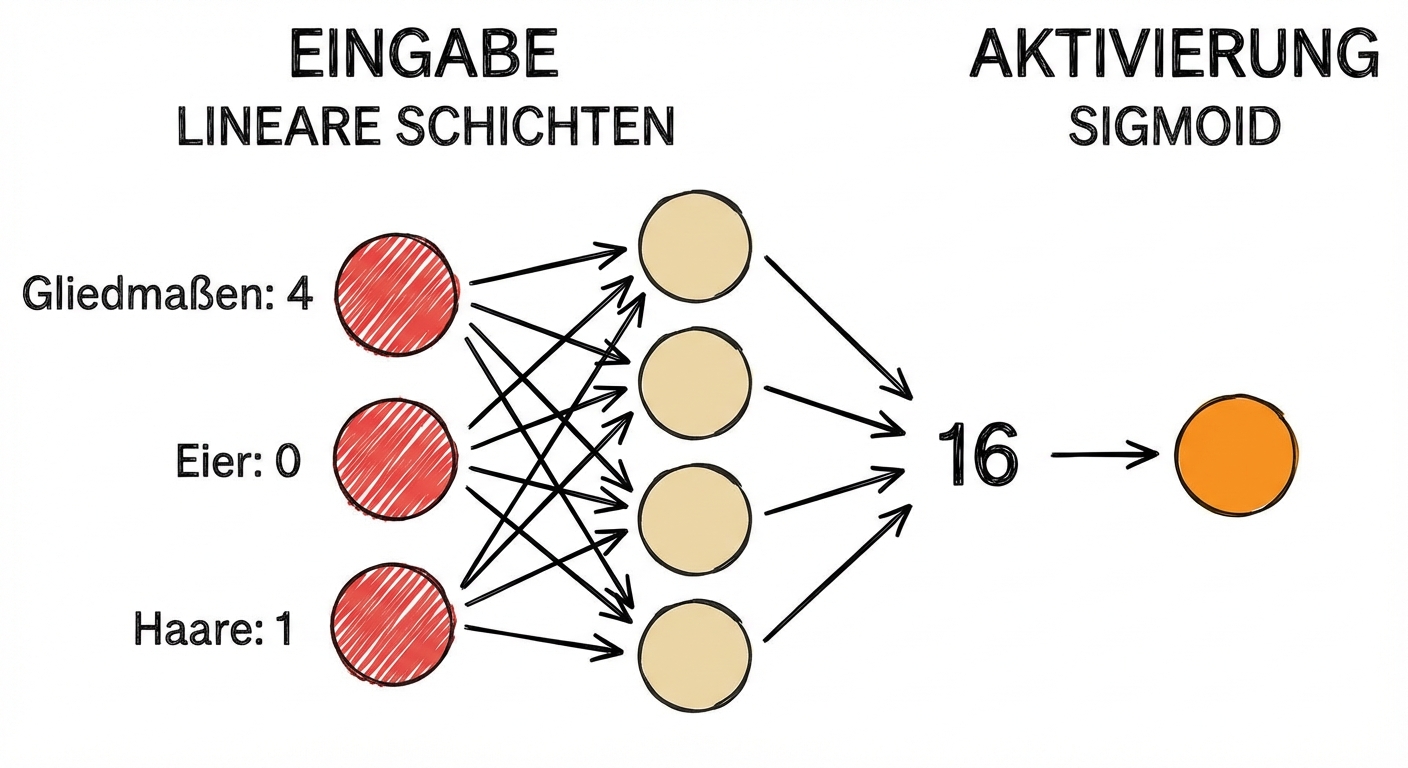
- Säugetier oder nicht?

- Wir geben den Ausgang der Voraktivierung (6) an die Sigmoid-Funktion weiter
Die Sigmoid-Funktion
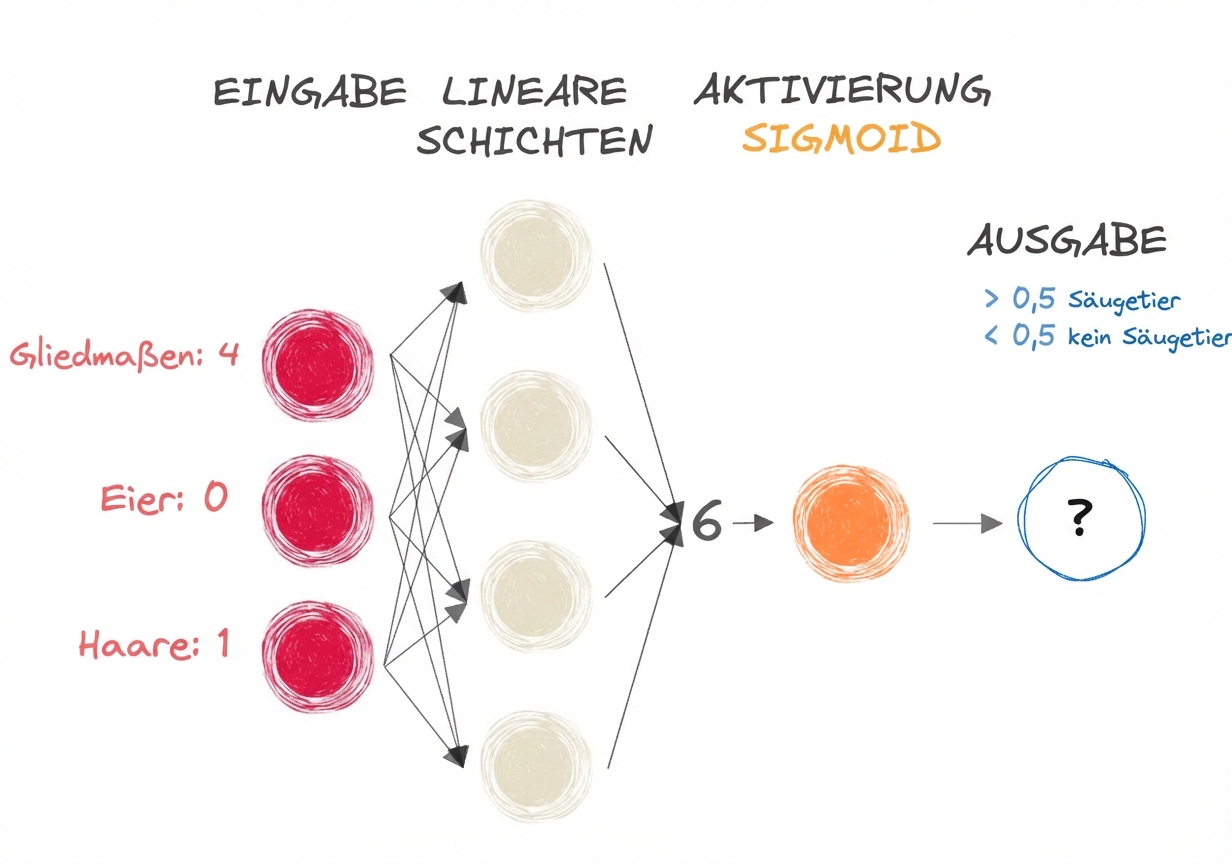
- Säugetier oder nicht?

- Wir geben den Ausgang der Voraktivierung (6) an die Sigmoid-Funktion weiter
Wir erhalten einen Wert zwischen 0 und 1
Wenn der Ausgang > 0,5 ist, ist das Klassenlabel = 1 (Säugetier)
- Wenn der Ausgang <= 0,5 ist, ist das Klassenlabel = 0 (kein Säugetier)
Die Sigmoid-Funktion
import torch import torch.nn as nn input_tensor = torch.tensor([[6]]) sigmoid = nn.Sigmoid()output = sigmoid(input_tensor) print(output)
tensor([[0.9975]])
Aktivierung als letzte Schicht
model = nn.Sequential(
nn.Linear(6, 4), # First linear layer
nn.Linear(4, 1), # Second linear layer
nn.Sigmoid() # Sigmoid activation function
)
Sigmoid als letzter Schritt in einem Netzwerk aus linearen Schichten entspricht der traditionellen logistischen Regression
Softmax kennenlernen
- Drei Klassen:
Softmax kennenlernen
- Drei Klassen:

Softmax kennenlernen
- Drei Klassen:

Softmax kennenlernen
- Drei Klassen:

Softmax kennenlernen
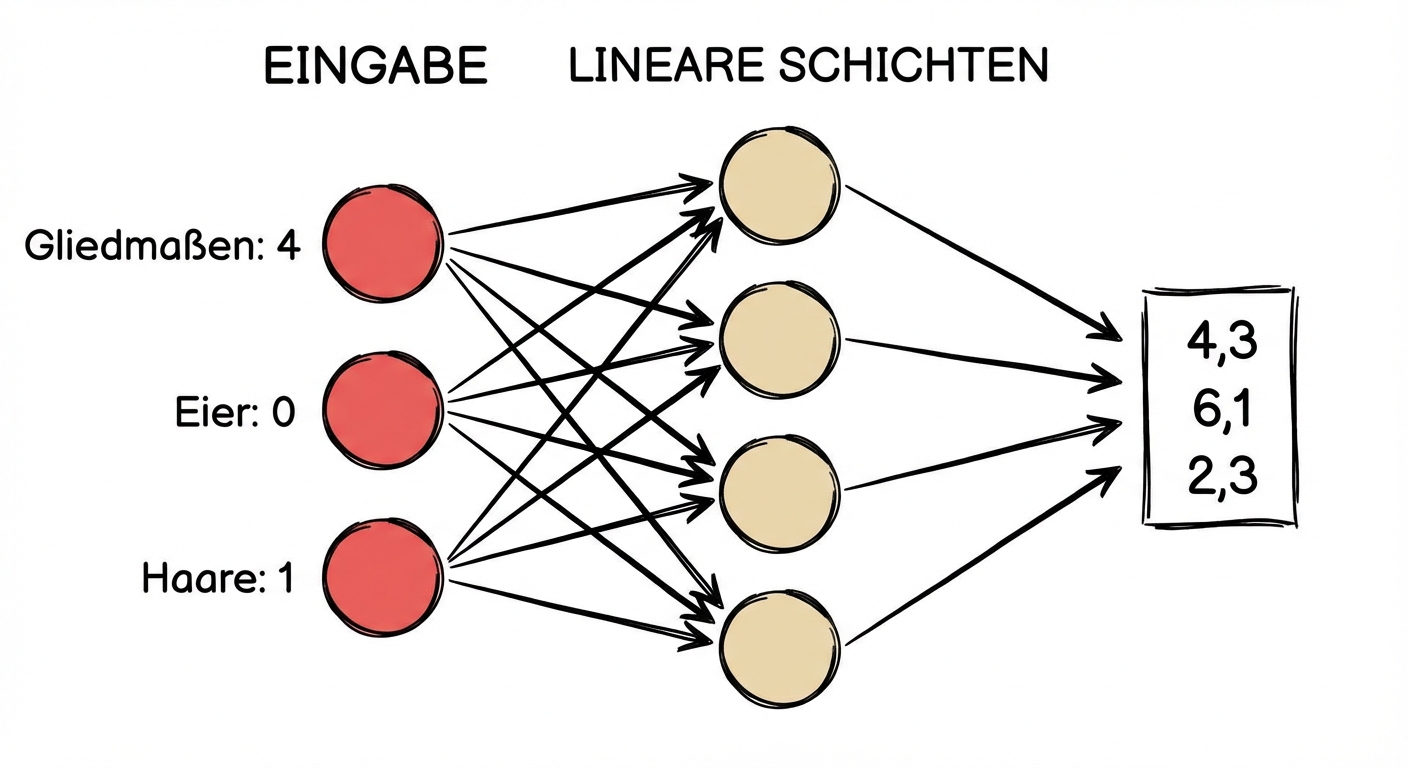
- Wählt dreidimensional als Eingabe und gibt die gleiche Form aus
Softmax kennenlernen
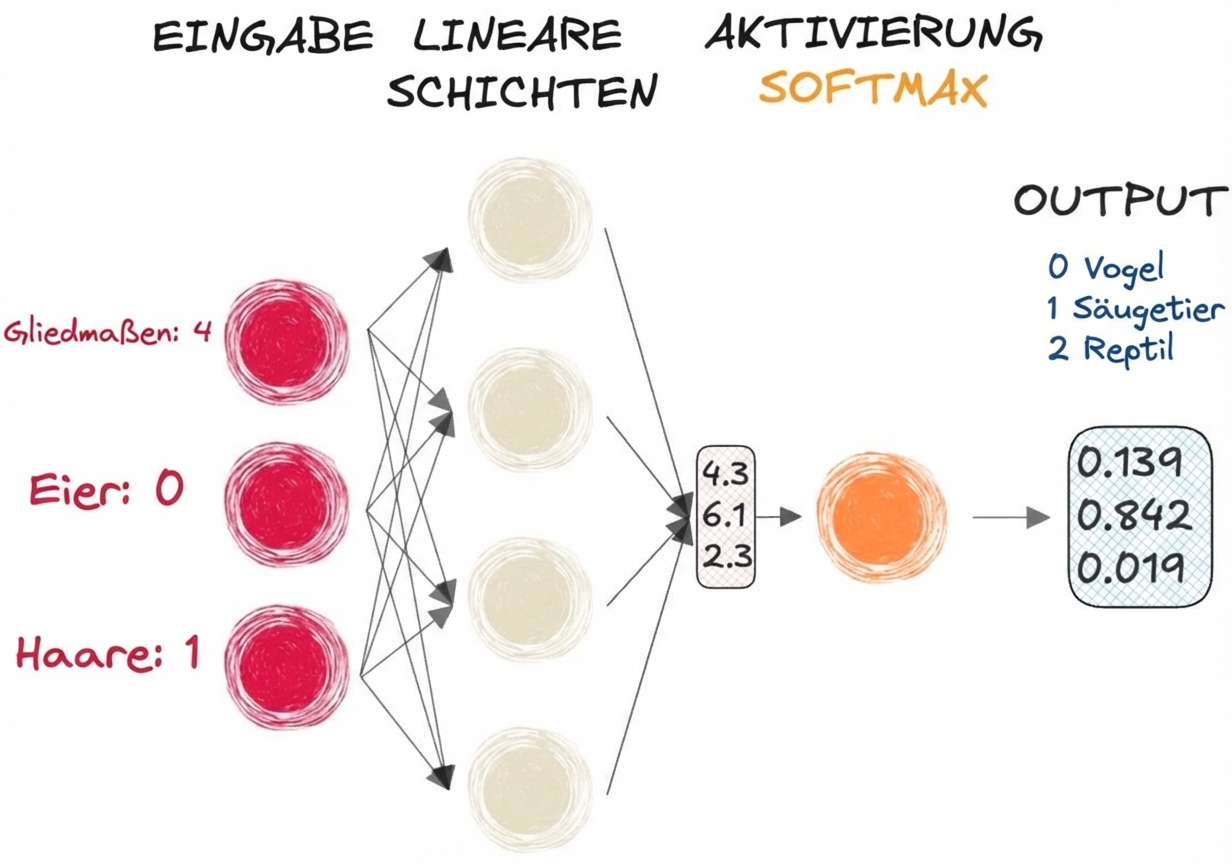
- Wählt dreidimensional als Eingabe und gibt die gleiche Form aus
- Gibt eine Wahrscheinlichkeitsverteilung aus:
- Jedes Element ist eine Wahrscheinlichkeit (sie liegt zwischen 0 und 1)
- Die Summe des Ausgangsvektors ist gleich 1
Softmax kennenlernen
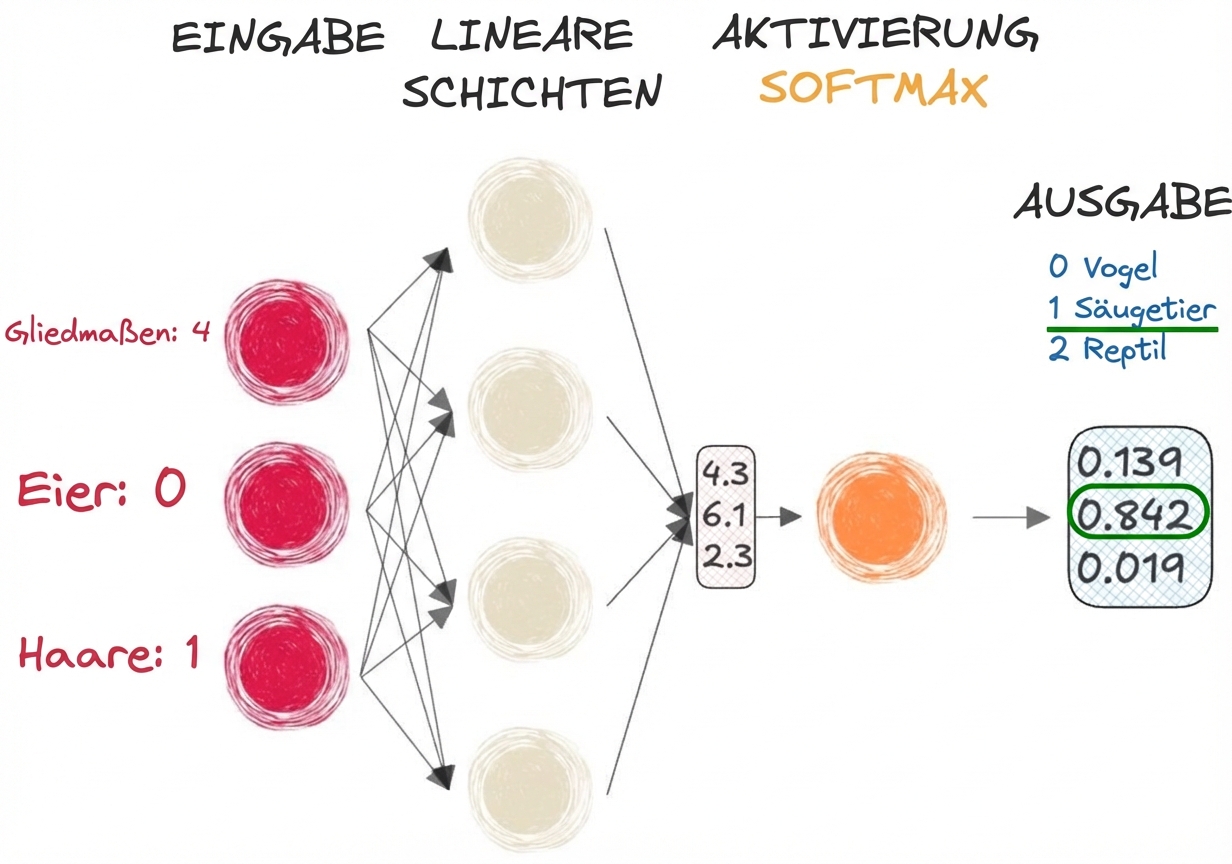
- Wählt dreidimensional als Eingabe und gibt die gleiche Form aus
- Gibt eine Wahrscheinlichkeitsverteilung aus:
- Jedes Element ist eine Wahrscheinlichkeit (sie liegt zwischen 0 und 1)
- Die Summe des Ausgangsvektors ist gleich 1
Softmax kennenlernen
import torch import torch.nn as nn # Create an input tensor input_tensor = torch.tensor( [[4.3, 6.1, 2.3]]) # Apply softmax along the last dimensionprobabilities = nn.Softmax(dim=-1) output_tensor = probabilities(input_tensor) print(output_tensor)
tensor([[0.1392, 0.8420, 0.0188]])
dim = -1gibt an, dass Softmax auf die letzte Dimension des Eingangstensors angewendet wirdnn.Softmax()kann als letzter Schritt innn.Sequential()genutzt werden
Lass uns üben!
Einführung in Deep Learning mit PyTorch

