Ableitungen zur Aktualisierung der Modellparameter verwenden

Einführung in Deep Learning mit PyTorch

Jasmin Ludolf

Senior Data Science Content Developer, DataCamp

Eine Analogie für Derivate

Die Ableitung stellt die Steigung der Kurve dar

Steile Steigung (rote Pfeile):
- Große Schritte, Ableitung ist hoch
Sanftere Steigung (grüne Pfeile):
- Kleine Schritte, Ableitung ist niedrig
Talboden (blauer Pfeil):
- Flach, Ableitung ist null

ein Bild von einem Tal

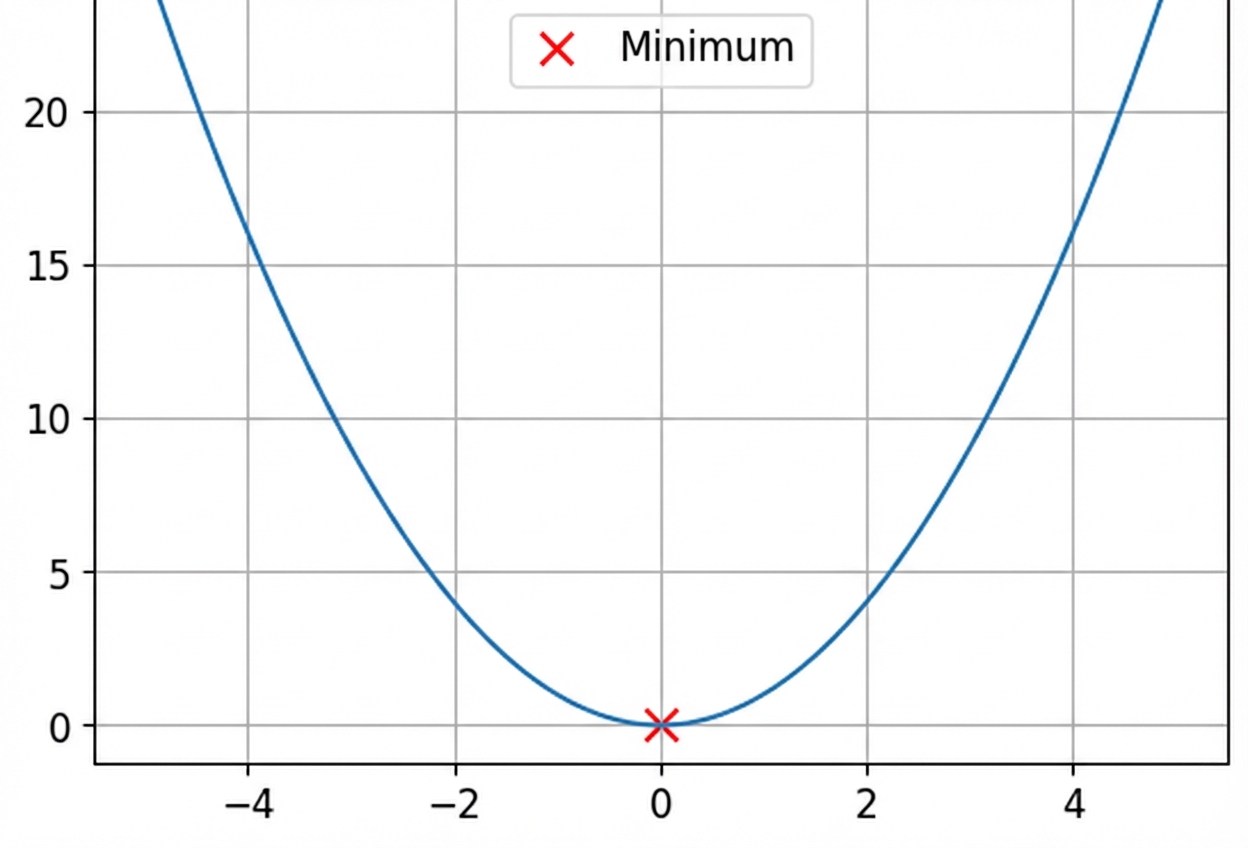
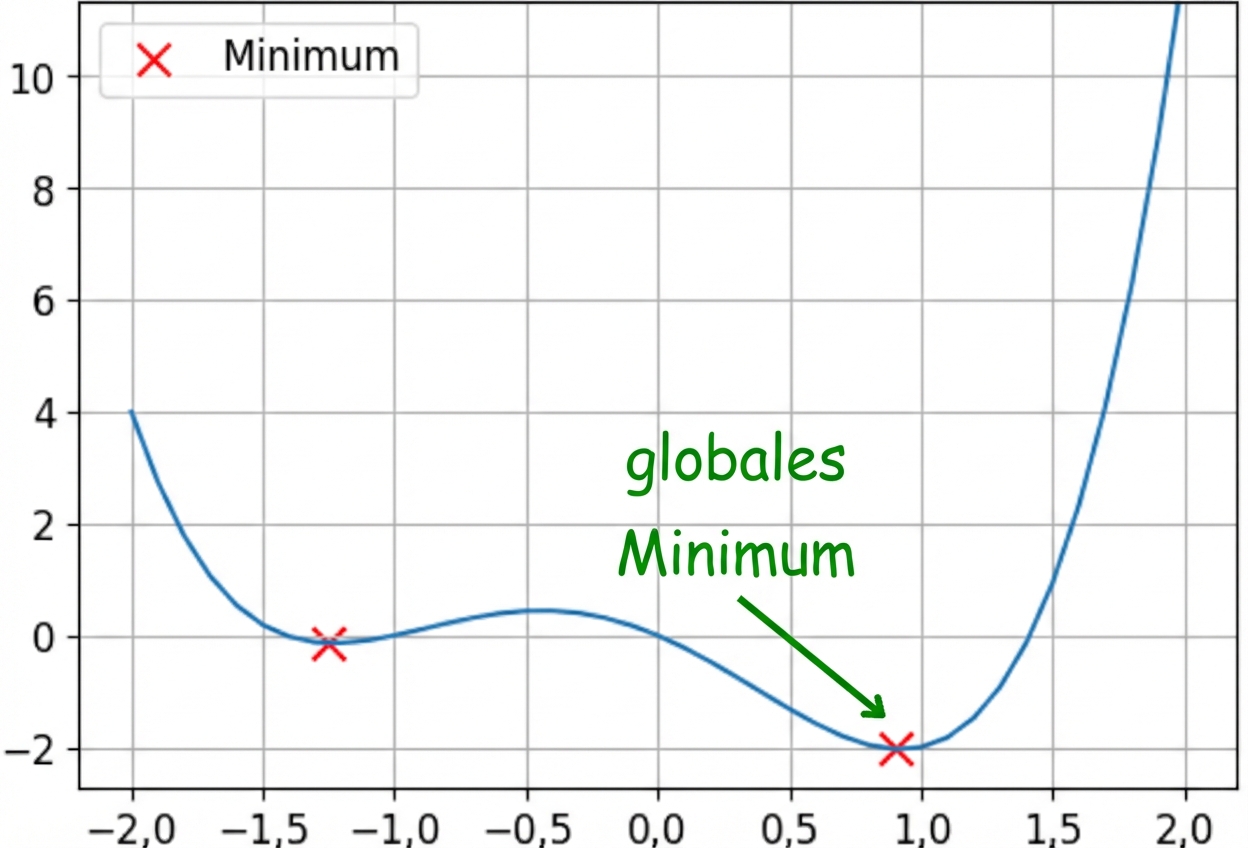
Konvexe und nicht-konvexe Funktionen

Dies ist eine konvexe Funktion

ein Beispiel für eine konvexe Funktion

Dies ist eine nicht-konvexe Funktion

ein Beispiel für eine nicht-konvexe Funktion mit globalem Minimum hervorgehoben

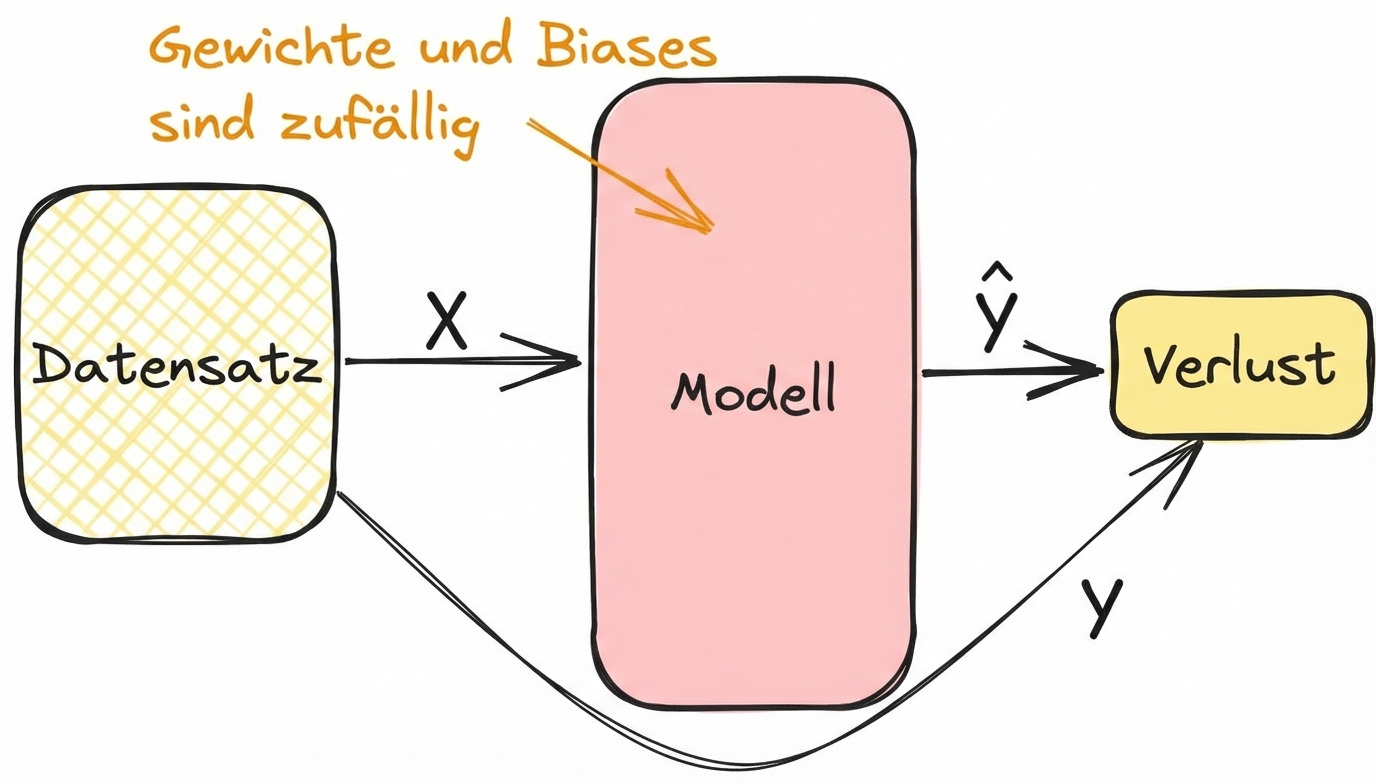
Derivate und Training von Modellen verbinden

Berechne den Verlust im Vorwärtsdurchlauf während des Trainings

$$ Berechnung des Verlustes

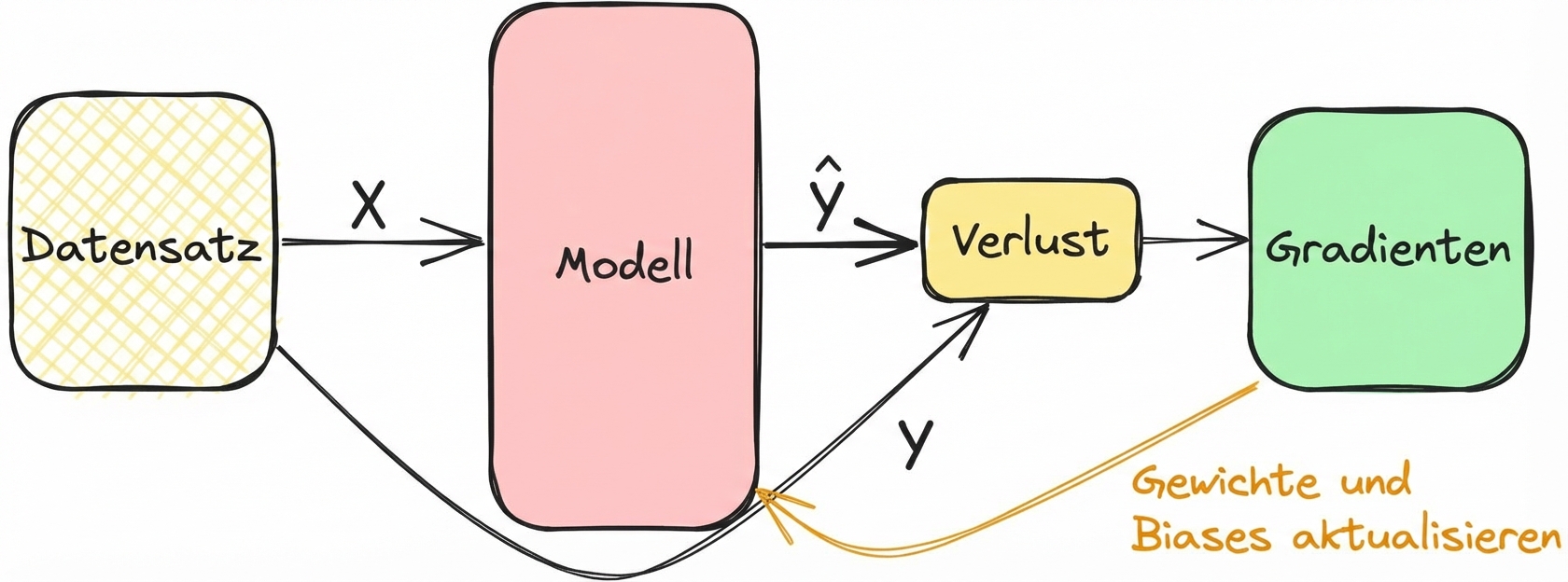
Derivate und Training von Modellen verbinden

Gradienten helfen, Verluste zu minimieren, Schichtgewichte und Verzerrungen abzustimmen
Wiederhole den Vorgang, bis die Schichten aufeinander abgestimmt sind

$$ Berechnung von Gradienten

Backpropagation-Konzepte

Stell dir ein Netz vor, das aus drei Schichten besteht:
- Fange mit Verlustgradienten für $L2$an
- Nutze $L2$, um $L1$ Gradienten zu berechnen.
- Wiederhole diesen Vorgang für alle Schichten ($L1$, $L0$)

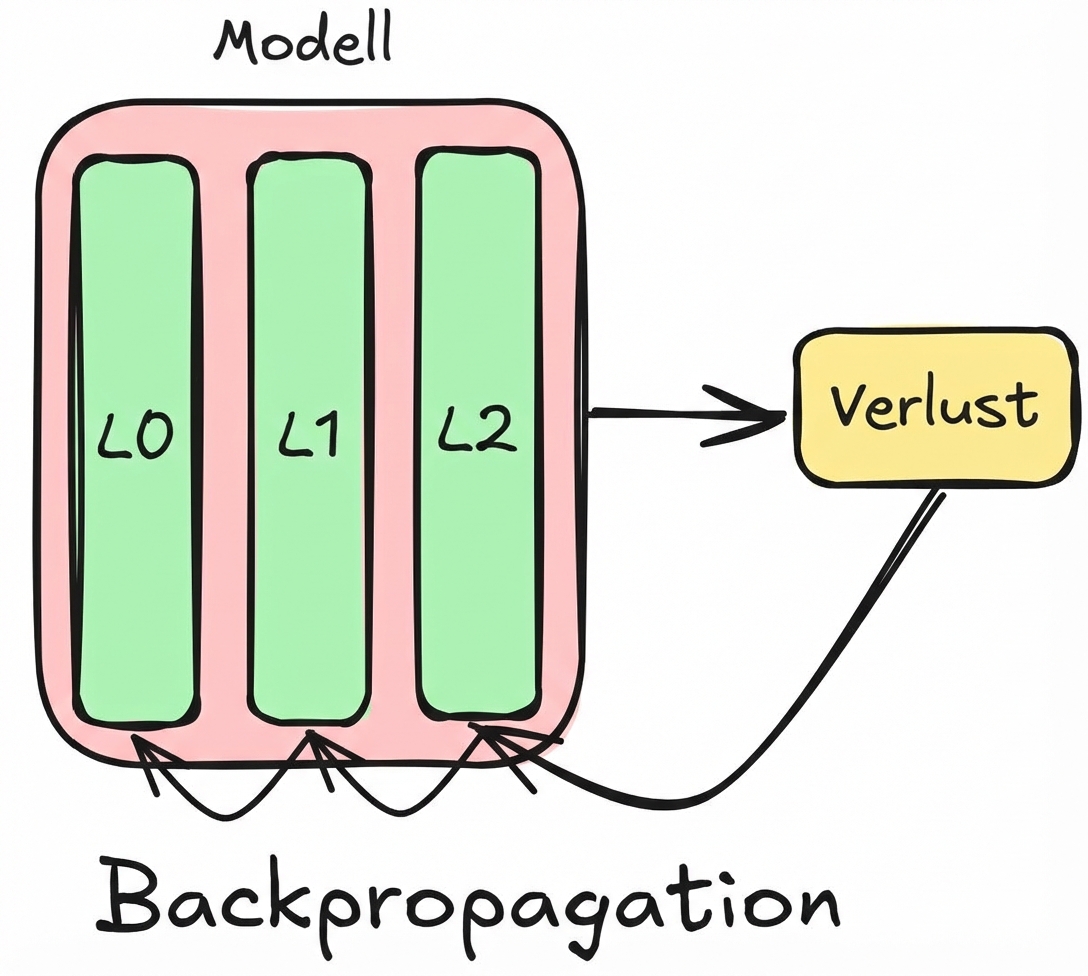
Darstellung einer Backpropagation

Backpropagation in PyTorch

# Run a forward pass 
model = nn.Sequential(nn.Linear(16, 8),
                      nn.Linear(8, 4),
                      nn.Linear(4, 2))
prediction = model(sample)


# Calculate the loss and gradients
criterion = CrossEntropyLoss()
loss = criterion(prediction, target)
loss.backward()

# Access each layer's gradients
model[0].weight.grad
model[0].bias.grad
model[1].weight.grad
model[1].bias.grad
model[2].weight.grad
model[2].bias.grad

Modellparameter manuell aktualisieren

# Learning rate is typically small
lr = 0.001

# Update the weights
weight = model[0].weight
weight_grad = model[0].weight.grad


weight = weight - lr * weight_grad


# Update the biases
bias = model[0].bias
bias_grad = model[0].bias.grad

bias = bias - lr * bias_grad

Auf jeden Schichtgradienten zugreifen
Mit der Lernrate multiplizieren
Dieses Produkt vom Gewicht abziehen

Gradientenabstieg

Für nicht-konvexe Funktionen verwenden wir den Gradientenabstieg
PyTorch vereinfacht dies mit Optimierern
- Stochastic Gradient Descent (SGD)

import torch.optim as optim

# Create the optimizer
optimizer = optim.SGD(model.parameters(), lr=0.001)


# Perform parameter updates
optimizer.step()

Lass uns üben!

Einführung in Deep Learning mit PyTorch