¿Qué probabilidad hay?
Introducción a la estadística en Python

Maggie Matsui
Content Developer, DataCamp
Medir la probabilidad
¿Cuál es la probabilidad de un suceso?
$$ P(\text{event}) = \frac{\text{\# ways event can happen}}{\text{total \# of possible outcomes}} $$
Ejemplo: lanzar una moneda
$$ P(\text{heads}) = \frac{\text{1 way to get heads}}{\text{2 possible outcomes}} = \frac{1}{2} = 50\%$$

Asignación de vendedores
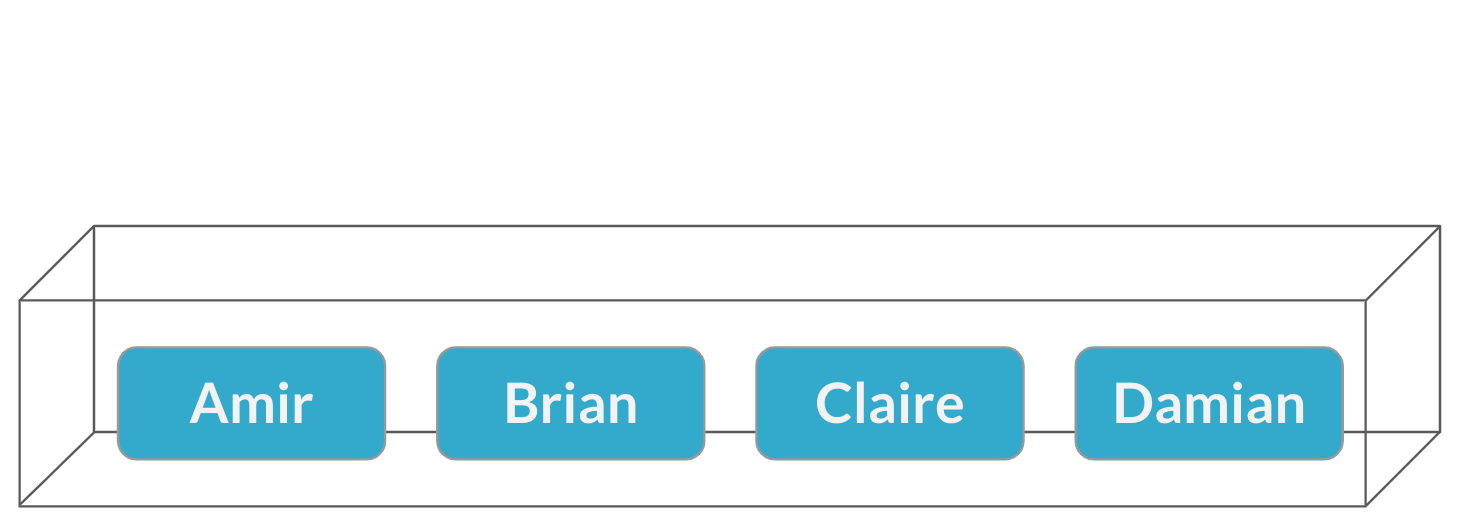
Asignación de vendedores
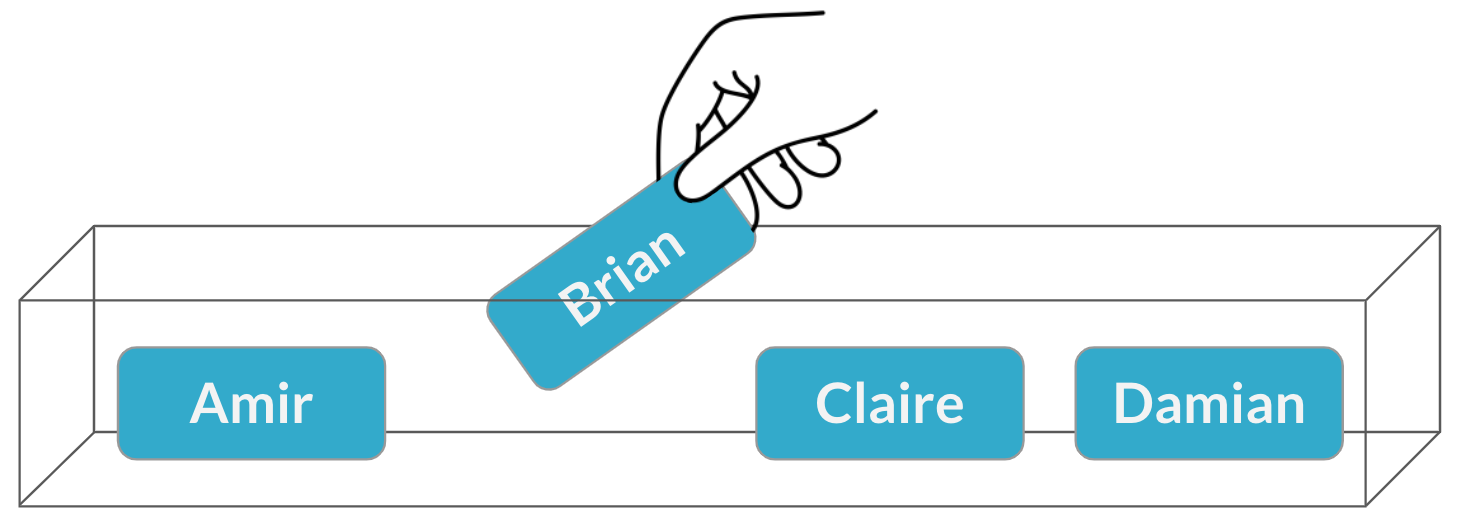
$$P(\text{Brian}) = \frac{1}{4} = 25\%$$
Muestreo de un DataFrame
print(sales_counts)
name n_sales
0 Amir 178
1 Brian 128
2 Claire 75
3 Damian 69
sales_counts.sample()
name n_sales
1 Brian 128
sales_counts.sample()
name n_sales
2 Claire 75
Establecer una semilla aleatoria
np.random.seed(10)sales_counts.sample()
name n_sales
1 Brian 128
np.random.seed(10)
sales_counts.sample()
name n_sales
1 Brian 128
np.random.seed(10)
sales_counts.sample()
name n_sales
1 Brian 128
Una segunda reunión
Muestreo sin sustitución

Una segunda reunión
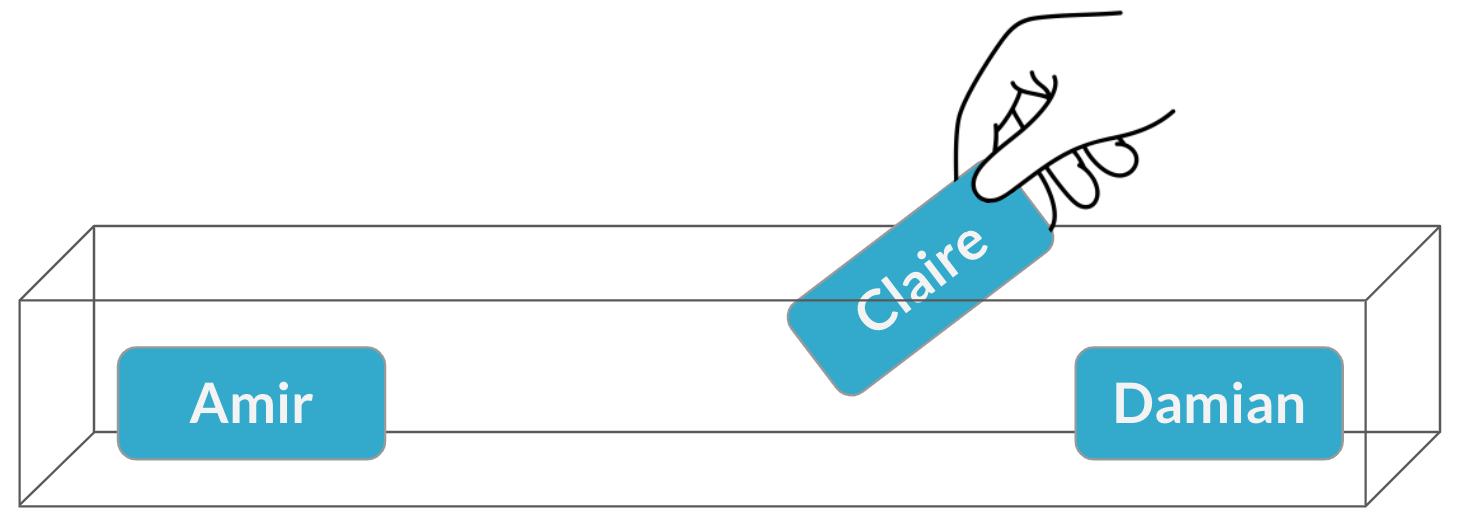
$$P(\text{Claire}) = \frac{1}{3} = 33\%$$
Muestreo doble en Python
sales_counts.sample(2)
name n_sales
1 Brian 128
2 Claire 75
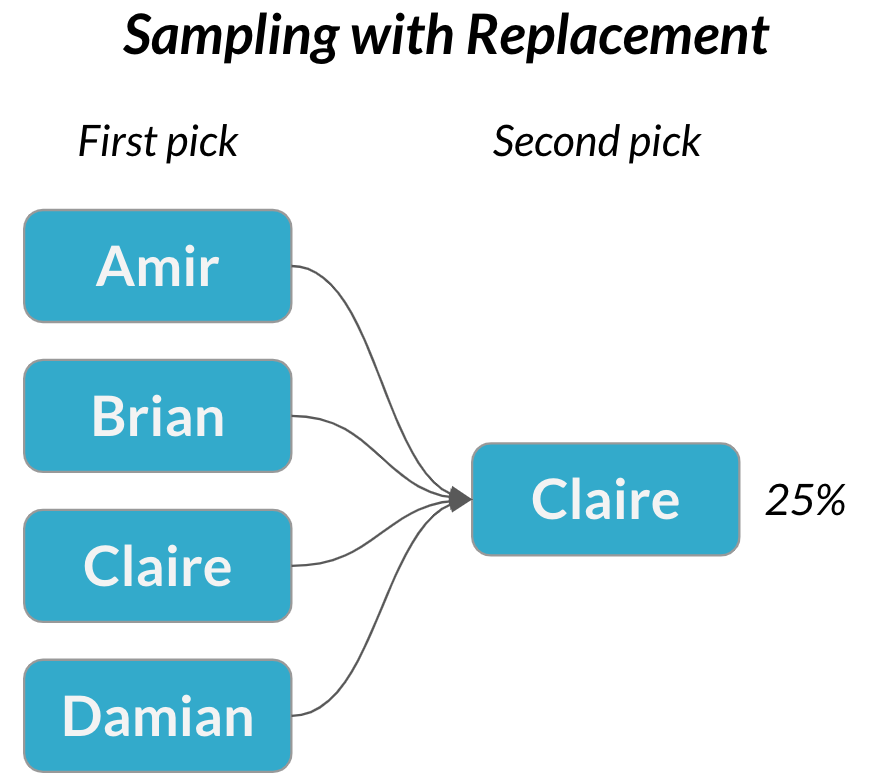
Muestreo con sustitución
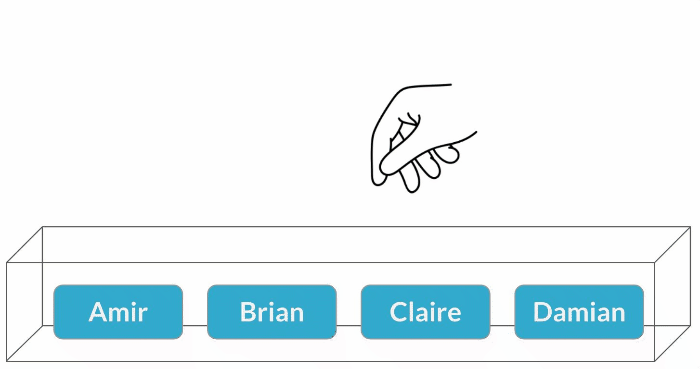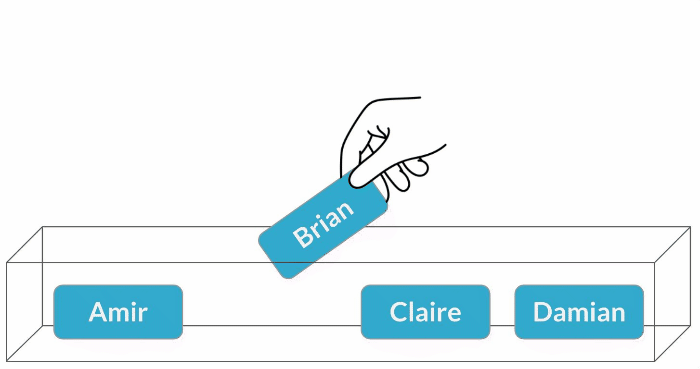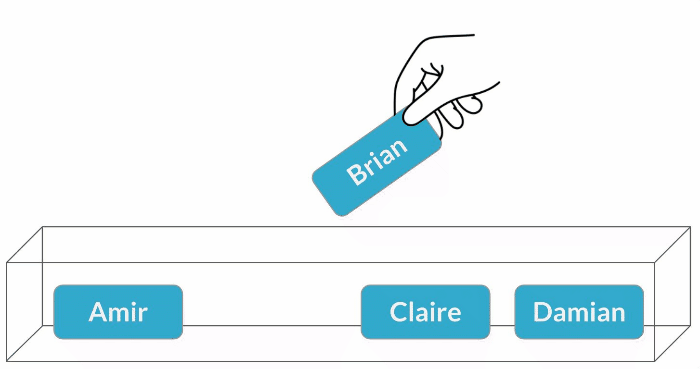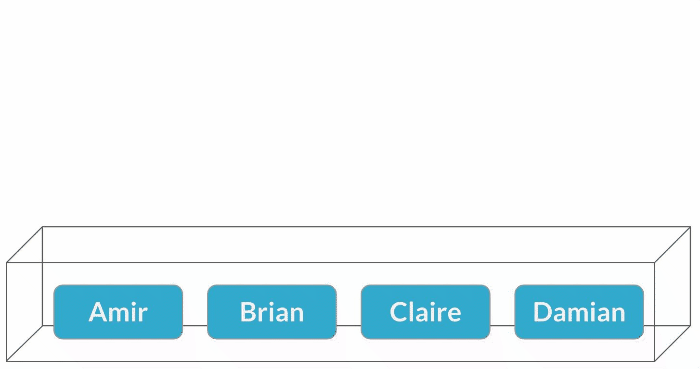
Muestreo con sustitución
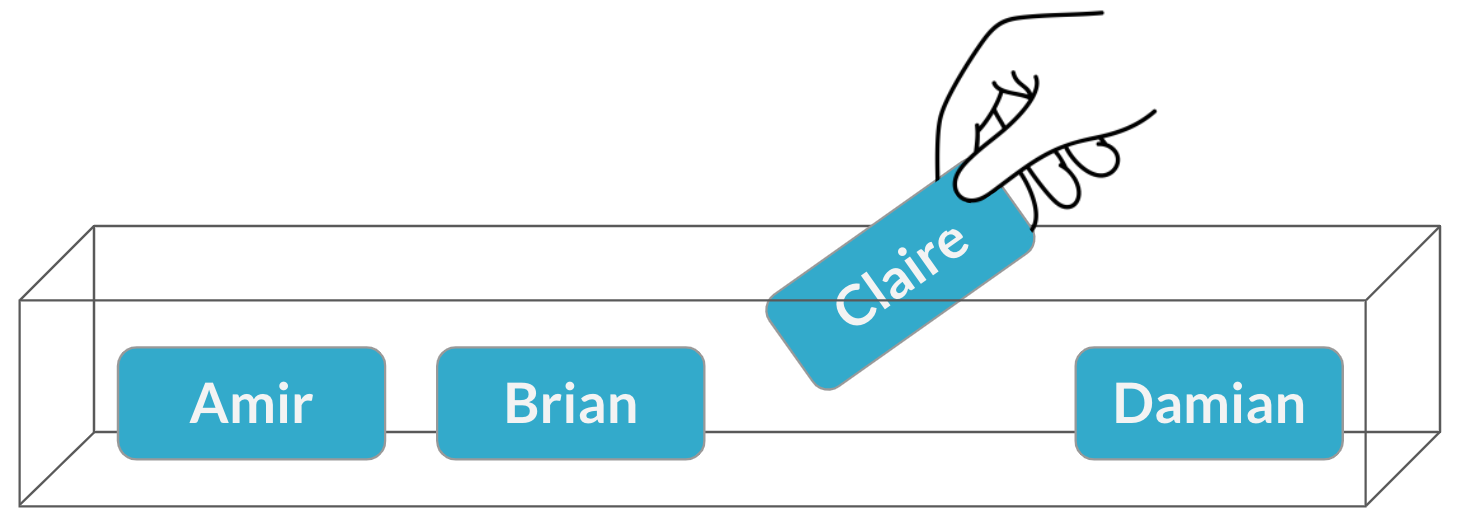
$$P(\text{Claire}) = \frac{1}{4} = 25\%$$
Muestreo con/sin sustitución en Python
sales_counts.sample(5, replace = True)
name n_sales
1 Brian 128
2 Claire 75
1 Brian 128
3 Damian 69
0 Amir 178
Sucesos independientes
Dos sucesos son independientes si la probabilidad del segundo suceso no se ve afectada por el resultado del primero.

Sucesos independientes
Dos sucesos son independientes si la probabilidad del segundo suceso no se ve afectada por el resultado del primero.
Muestreo con sustitución = cada selección es independiente
Hechos dependientes
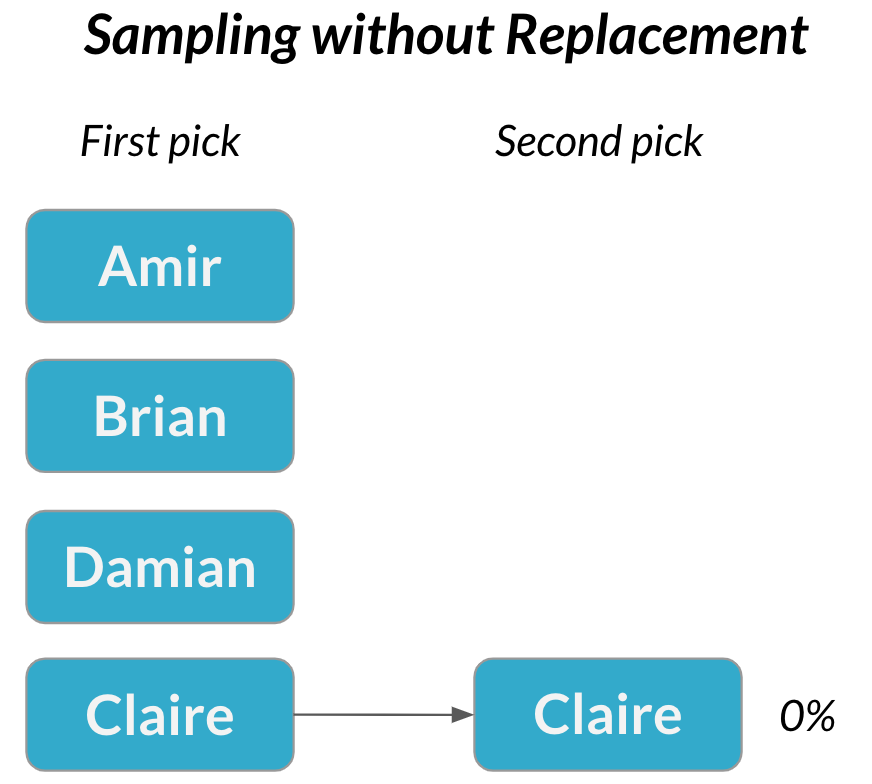
Dos sucesos son dependientes si la probabilidad del segundo suceso sí se ve afectada por el resultado del primero.

Hechos dependientes
Dos sucesos son dependientes si la probabilidad del segundo suceso sí se ve afectada por el resultado del primero.
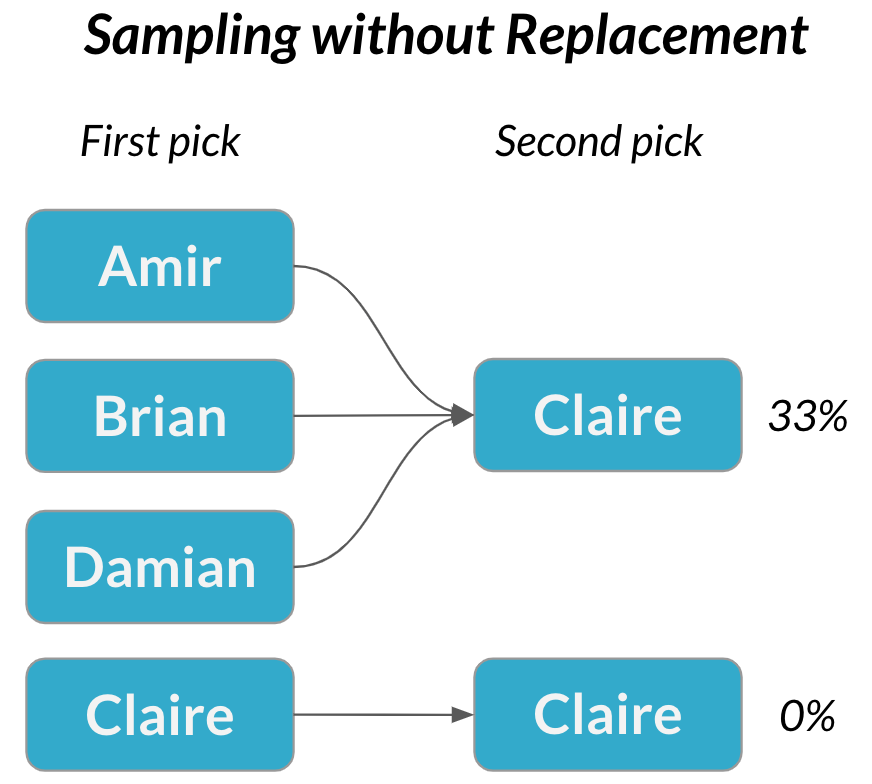
Hechos dependientes
Dos sucesos son dependientes si la probabilidad del segundo suceso sí se ve afectada por el resultado del primero.
Muestreo sin sustitución → las selecciones se vuelven dependientes
¡Vamos a practicar!
Introducción a la estadística en Python

