La distribución binomial

Introducción a la estadística en Python

Maggie Matsui

Content Developer, DataCamp

Lanzar una moneda

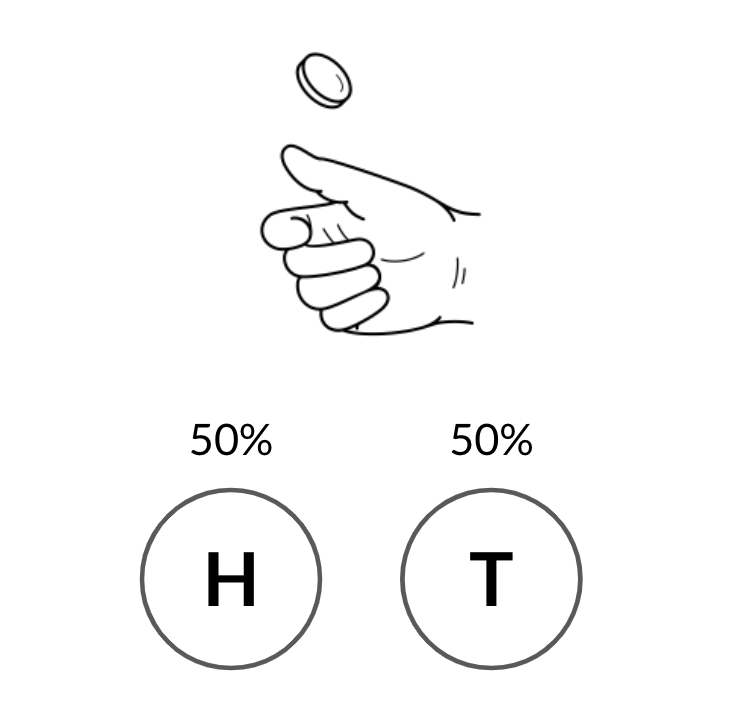
Una mano lanza una moneda, que tiene un 50 % de probabilidad de salir cara H y un 50 % de probabilidad de salir cruz T

Introducción a la estadística en Python

Resultados binarios

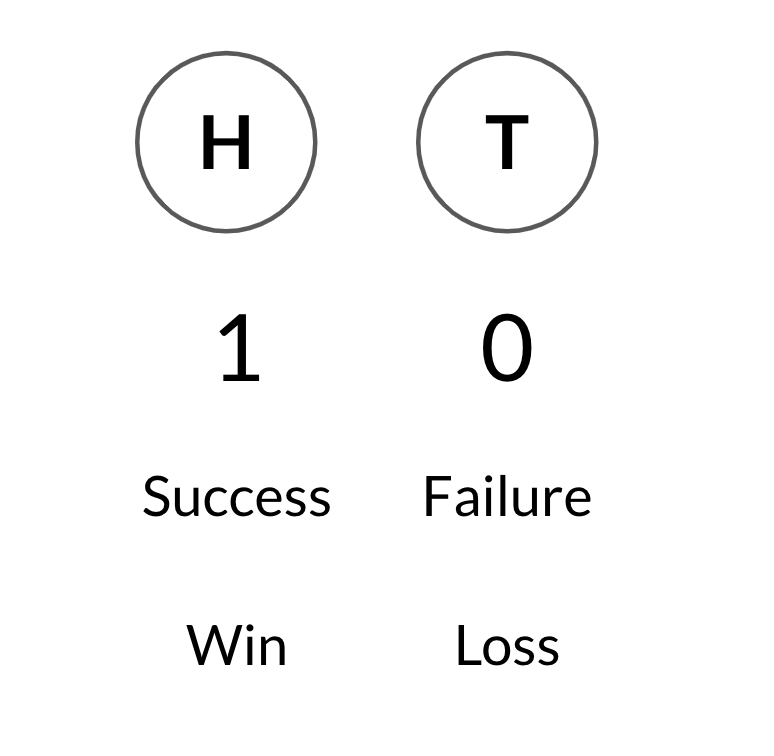
H y T, 1 y 0, acierto y fallo, ganar y perder

Introducción a la estadística en Python

Un solo lanzamiento

binom.rvs(# of coins, probability of heads/success, size=# of trials)

1 = cara, 0 = cruz

from scipy.stats import binom

binom.rvs(1, 0.5, size=1)

array([1])
Introducción a la estadística en Python

Una tirada muchas veces

binom.rvs(1, 0.5, size=8)

array([0, 1, 1, 0, 1, 0, 1, 1])

 

binom.rvs(1, 0.5, 8) con 1 en rojo, 0.5 en amarillo, 8 en azul. Texto: Se lanza 1 (en rojo) moneda con un 50 % (en amarillo) de posibilidades de acierto 8 (en azul) veces

Introducción a la estadística en Python

Muchas tiradas una vez

binom.rvs(8, 0.5, size=1)

array([5])

 

binom.rvs(8, 0.5, size=1) con 8 en rojo, 0.5 en amarillo, 1 en azul. Texto: Se lanzan 8 (en rojo) monedas con un 50 % (en amarillo) de posibilidades de acierto 1 (en azul) vez

Introducción a la estadística en Python

Muchos lanzamiento muchas veces

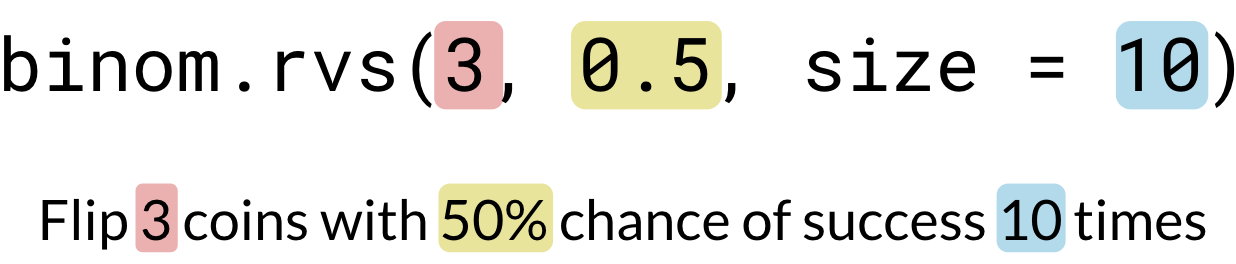
binom.rvs(3, 0.5, size=10)

array([0, 3, 2, 1, 3, 0, 2, 2, 0, 0])

 

binom.rvs(3, 0.5, size=10) con 3 en rojo, 0.5 en amarillo, 10 en azul. Texto: Se lanzan 3 (en rojo) monedas con un 50 % (en amarillo) de posibilidades de acierto 10 (en azul) veces

Introducción a la estadística en Python

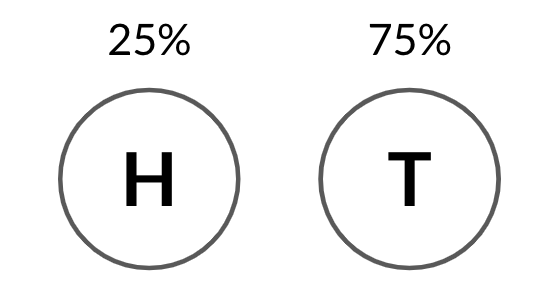
Otras probabilidades

binom.rvs(3, 0.25, size=10)

array([1, 1, 1, 1, 0, 0, 2, 0, 1, 0])

 

Imagen de cara con 25 % de probabilidad y cruz con 75 % de probabilidad

Introducción a la estadística en Python

Distribución binomial

Distribución de probabilidad del número de aciertos en una secuencia de intentos independientes

Ejemplo: número de caras en una secuencia de lanzar una moneda

Descrito por $n$ y $p$

  • $n$: número total de intentos
  • $p$: probabilidad de acierto
binom.rvs(n=10, p=0.5, size=20)

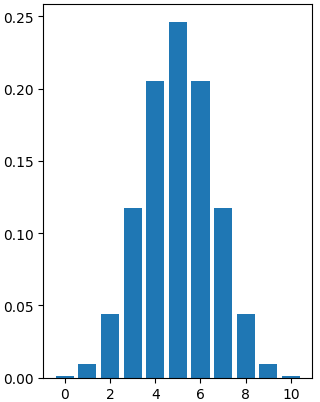
Gráfico de la distribución binomial con n=10, p = 0.5

Introducción a la estadística en Python

¿Cuál es la probabilidad de 7 caras?

$P(\text{heads} = 7)$

# binom.pmf(num heads, num trials, prob of heads)
binom.pmf(7, 10, 0.5)

0.1171875
Introducción a la estadística en Python

¿Cuál es la probabilidad de 7 caras o menos?

$P(\text{heads} \le 7)$

binom.cdf(7, 10, 0.5)

0.9453125
Introducción a la estadística en Python

¿Cuál es la probabilidad de que salgan más de 7 caras?

$P(\text{heads} > 7)$

1 - binom.cdf(7, 10, 0.5)

0.0546875
Introducción a la estadística en Python

Valor esperado

$\text{Expected value} = n \times p$

Número esperado de caras tras 10 tiradas $= 10 \times 0,5 = 5$

Introducción a la estadística en Python

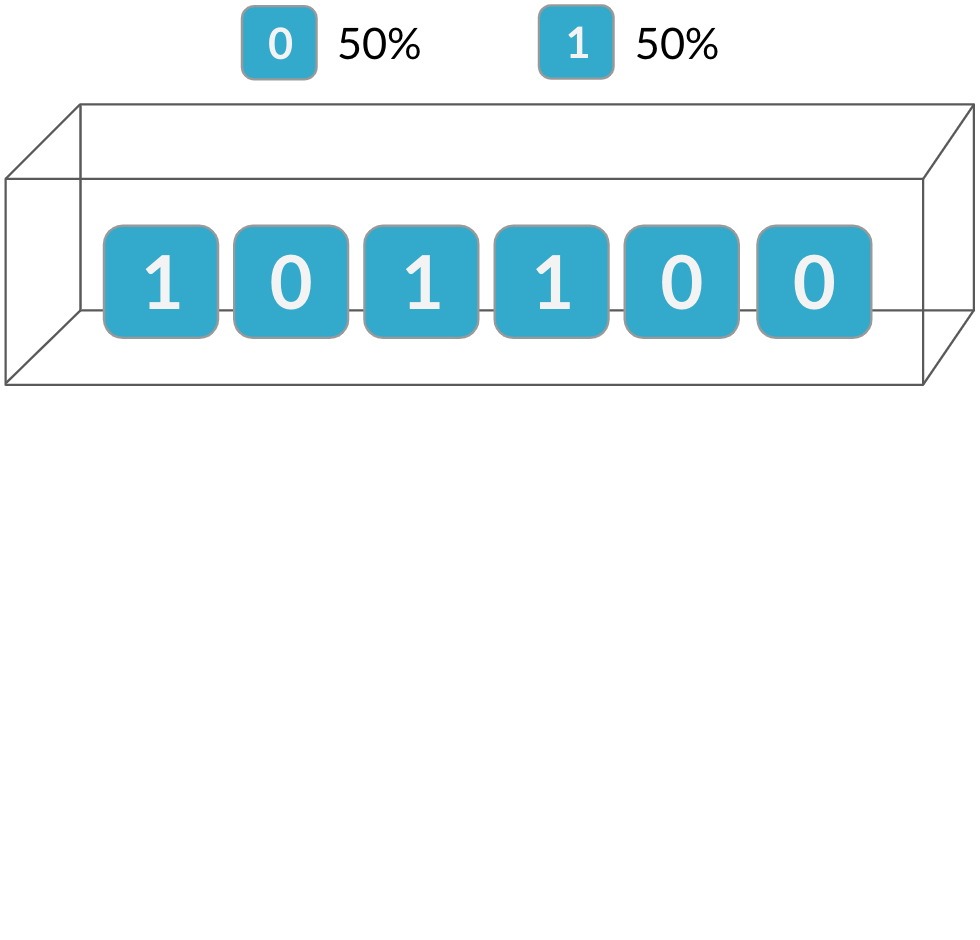
Independencia

La distribución binomial es una distribución de probabilidad del número de aciertos en una secuencia de intentos independientes

Caja de tickets con 3 ceros y 3 unos. 50 % de probabilidad de 0, 50 % de probabilidad de 1

Introducción a la estadística en Python

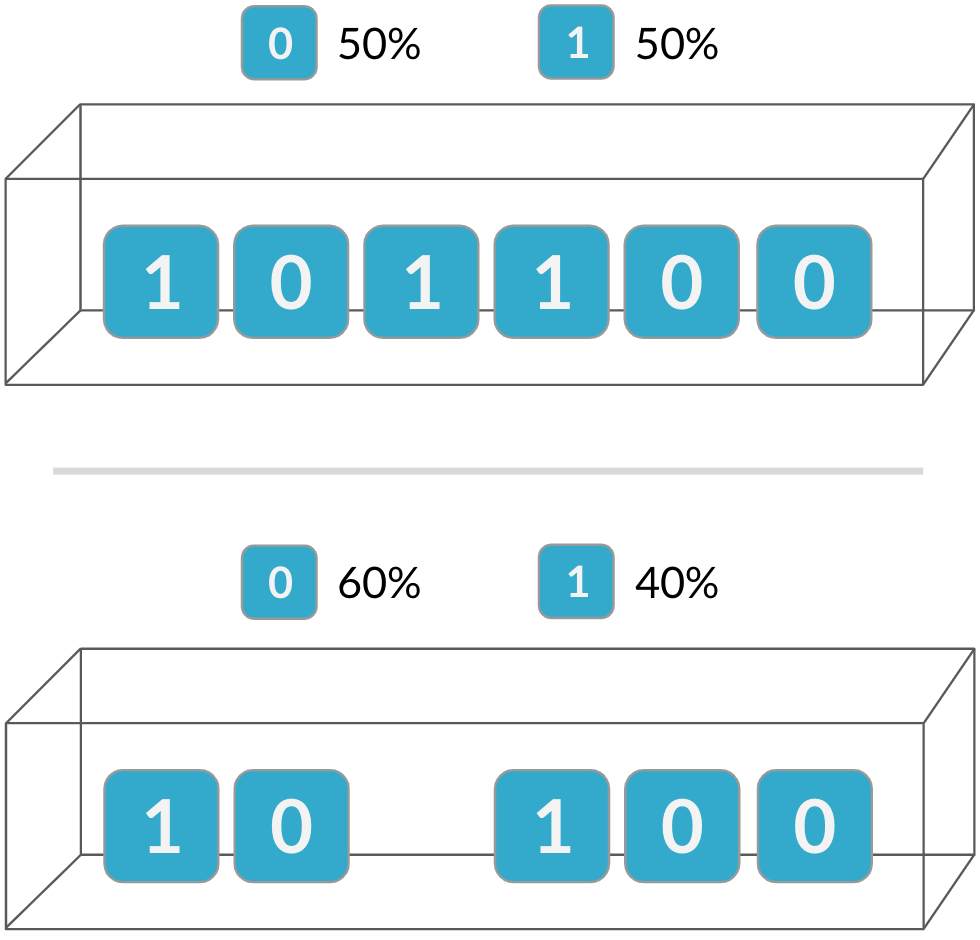
Independencia

La distribución binomial es una distribución de probabilidad del número de aciertos en una secuencia de intentos independientes

 

Las probabilidades del segundo intento cambian debido al resultado del primero.

 

Si los intentos no son independientes, no se aplica la distribución binomial.

Caja de tickets con 3 ceros y 2 unos. 60 % de probabilidad de 0, 40 % de probabilidad de 1

Introducción a la estadística en Python

¡Vamos a practicar!

Introducción a la estadística en Python

Preparing Video For Download...