Medidas de dispersión

Introducción a la estadística en Python

Maggie Matsui

Content Developer, DataCamp

¿Qué es la difusión?

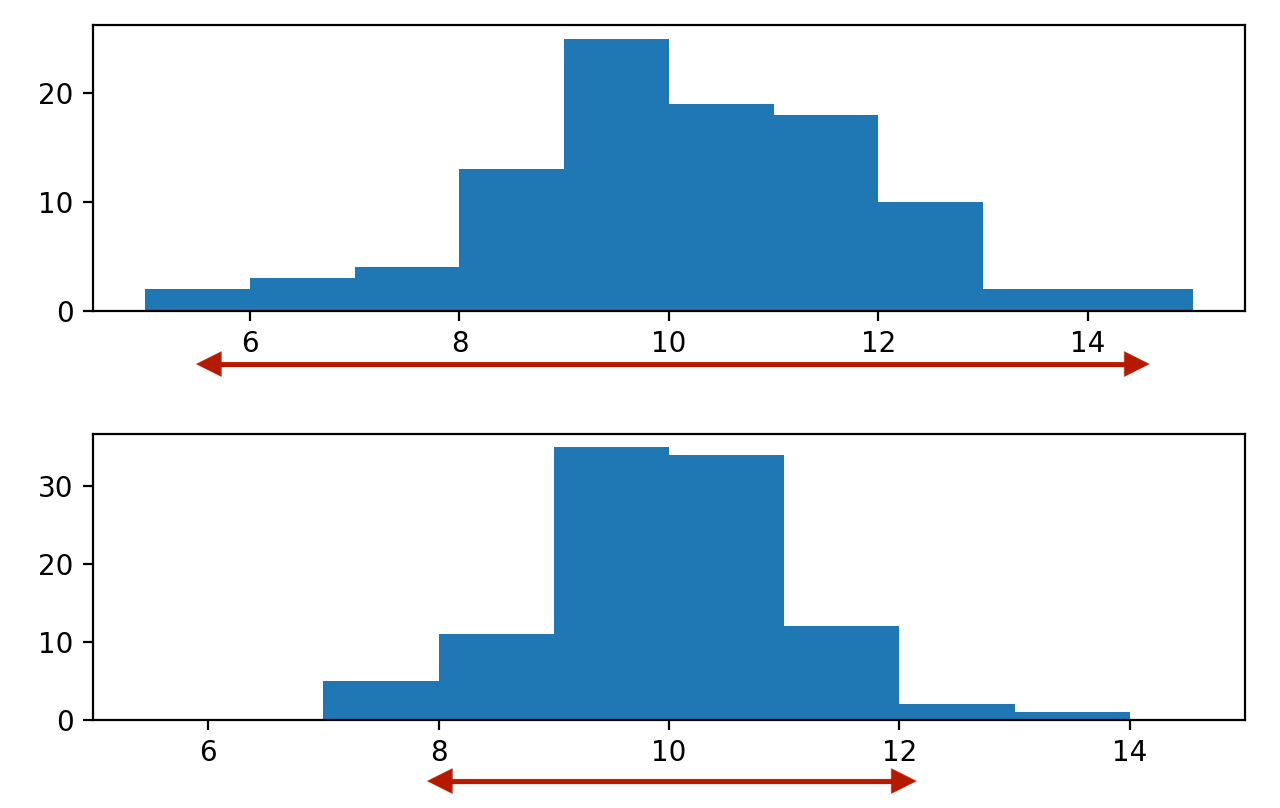
Dos histogramas: uno estrecho, con datos que abarcan pocos valores, y otro más ancho, con datos que abarcan más valores

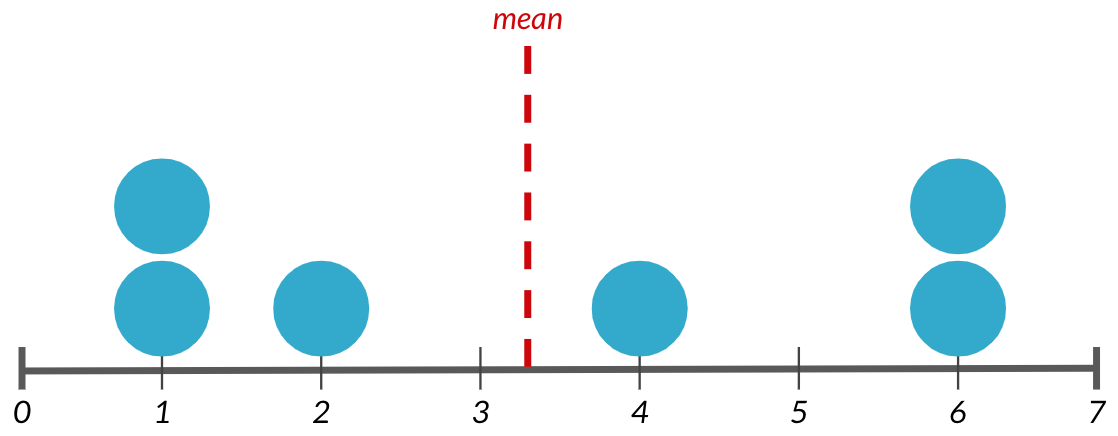
Varianza

Distancia promedio de cada punto de datos a la media de los datos

Un gráfico de puntos de 7 puntos de datos con una línea roja en el centro que representa la media.

Varianza

Distancia promedio de cada punto de datos a la media de los datos

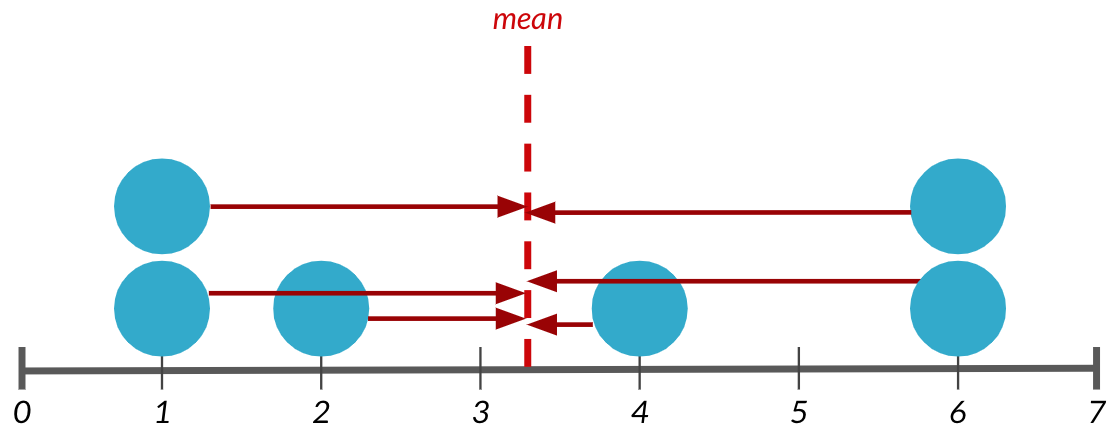
Un gráfico de puntos de 7 puntos de datos con una línea roja en el centro que representa la media. Se dibujan flechas entre cada punto y la línea media.

Cálculo de la varianza

1. Se resta la media de cada punto de datos

dists = msleep['sleep_total'] - 
        np.mean(msleep['sleep_total'])
print(dists)

0     1.666265
1     6.566265
2     3.966265
3     4.466265
4    -6.433735
      ...

2. Se eleva cada distancia al cuadrado

sq_dists = dists ** 2
print(sq_dists)

0      2.776439
1     43.115837
2     15.731259
3     19.947524
4     41.392945
      ...

Cálculo de la varianza

3. Se suma las distancias al cuadrado

sum_sq_dists = np.sum(sq_dists)
print(sum_sq_dists)

1624.065542

4. Se divide entre el número de puntos de datos - 1

variance = sum_sq_dists / (83 - 1)
print(variance)

19.805677

Se utiliza np.var()

np.var(msleep['sleep_total'], ddof=1)

19.805677

Sin ddof=1, se calcula la varianza de la población en lugar de la varianza de la muestra:

np.var(msleep['sleep_total'])

19.567055

Desviación típica

np.sqrt(np.var(msleep['sleep_total'], ddof=1))

4.450357

np.std(msleep['sleep_total'], ddof=1)

4.450357

Desviación media absoluta

dists = msleep['sleep_total'] - np.mean(msleep['sleep_total'])

np.mean(np.abs(dists))

3.566701

Desviación típica frente a desviación media absoluta

La desviación típica eleva al cuadrado las distancias y penaliza más las distancias largas que las cortas.
La desviación media absoluta penaliza cada distancia por igual.
Ninguna es mejor que la otra, pero la típica es más común que la media absoluta.

Cuantiles

np.quantile(msleep['sleep_total'], 0.5)

10.1

cuantil 0.5 = mediana

Cuartiles:

np.quantile(msleep['sleep_total'], [0, 0.25, 0.5, 0.75, 1])

array([ 1.9 ,  7.85, 10.1 , 13.75, 19.9 ])

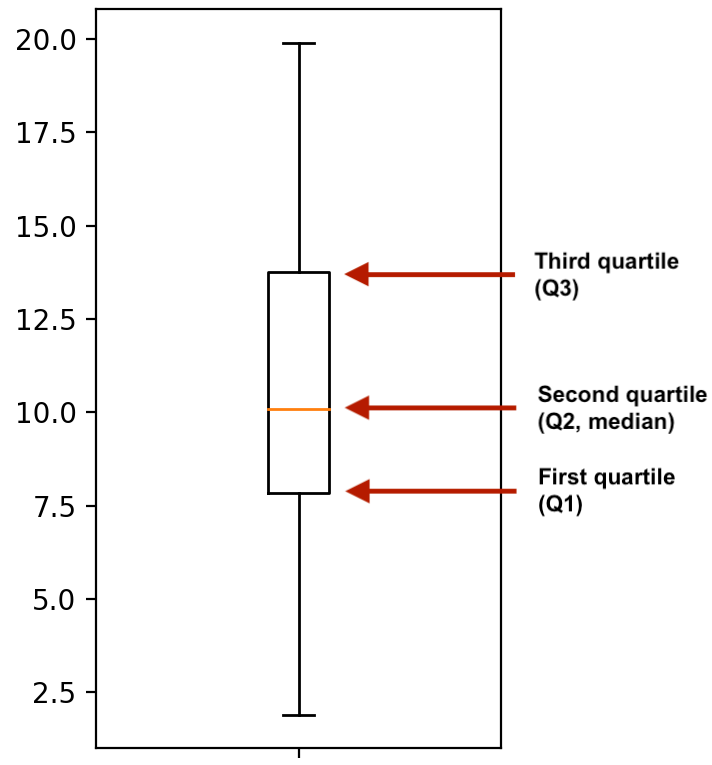
Los diagramas de caja utilizan cuartiles

import matplotlib.pyplot as plt
plt.boxplot(msleep['sleep_total'])
plt.show()

sleep_total boxplot.png

Cuantiles con np.linspace()

np.quantile(msleep['sleep_total'], [0, 0.2, 0.4, 0.6, 0.8, 1])

array([ 1.9 ,  6.24,  9.48, 11.14, 14.4 , 19.9 ])

np.linspace(start, stop, num)

np.quantile(msleep['sleep_total'], np.linspace(0, 1, 5))

array([ 1.9 ,  7.85, 10.1 , 13.75, 19.9 ])

Intervalo intercuartílico (IQR)

Altura de la caja en un diagrama de caja

np.quantile(msleep['sleep_total'], 0.75) - np.quantile(msleep['sleep_total'], 0.25)

5.9

from scipy.stats import iqr
iqr(msleep['sleep_total'])

5.9

Valores atípicos

Valor atípico: punto de datos que difiere sustancialmente de los demás

¿Cómo sabemos qué es una diferencia sustancial? Un punto de datos es un valor atípico si:

$\text{data} < \text{Q1} - 1.5\times\text{IQR}$ o
$\text{data} > \text{Q3} + 1.5\times\text{IQR}$

Encontrar valores atípicos

from scipy.stats import iqr
iqr = iqr(msleep['bodywt'])

lower_threshold = np.quantile(msleep['bodywt'], 0.25) - 1.5 * iqr
upper_threshold = np.quantile(msleep['bodywt'], 0.75) + 1.5 * iqr

msleep[(msleep['bodywt'] < lower_threshold) | (msleep['bodywt'] > upper_threshold)]

                    name   vore  sleep_total    bodywt
4                    Cow  herbi          4.0   600.000
20        Asian elephant  herbi          3.9  2547.000
22                 Horse  herbi          2.9   521.000
...

Todo a la vez

msleep['bodywt'].describe()

count      83.000000
mean      166.136349
std       786.839732
min         0.005000
25%         0.174000
50%         1.670000
75%        41.750000
max      6654.000000
Name: bodywt, dtype: float64

¡Vamos a practicar!

Introducción a la estadística en Python