Correlación
Introducción a la estadística en Python

Maggie Matsui
Content Developer, DataCamp
Relaciones entre dos variables
- x = variable independiente/explicativa
- y = variable dependiente/respuesta
Coeficiente de correlación
- Cuantifica la relación lineal entre dos variables
- Número entre -1 y 1
- La magnitud corresponde a la fuerza de la relación
- El signo (+ o -) corresponde a la dirección de la relación
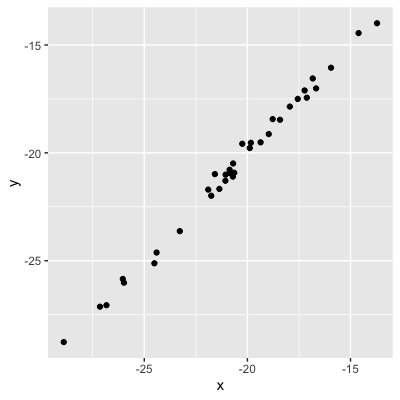
Magnitud = fuerza de la relación
0,99 (relación muy fuerte)
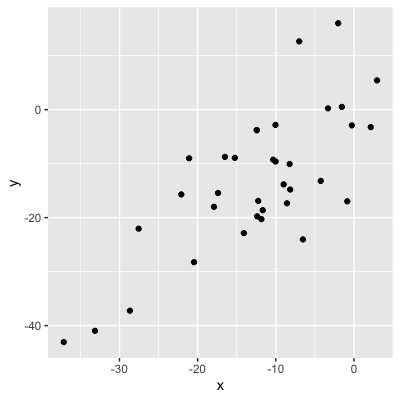
Magnitud = fuerza de la relación
0,99 (relación muy fuerte)

0,75 (relación fuerte)
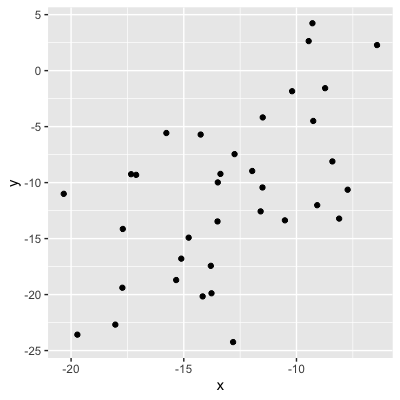
Magnitud = fuerza de la relación
0,56 (relación moderada)
Magnitud = fuerza de la relación
0,56 (relación moderada)

0,21 (relación débil)
Magnitud = fuerza de la relación
0,04 (sin relación)
- Conocer el valor de
xno nos dice nada sobrey
Signo = dirección
0,75: cuando aumenta x, aumenta y

-0.75: cuando aumenta x, disminuye y
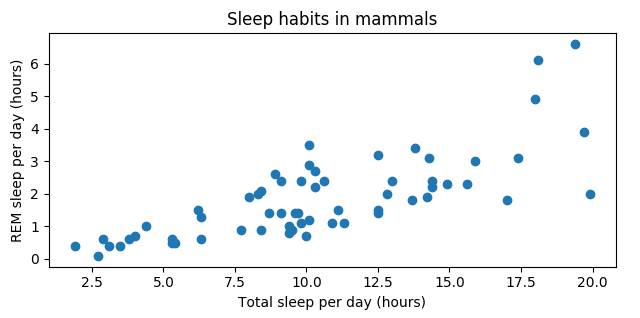
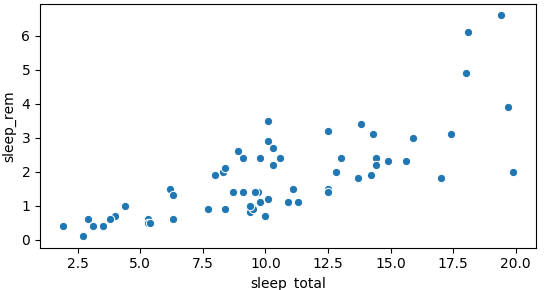
Visualizar las relaciones
import seaborn as snssns.scatterplot(x="sleep_total", y="sleep_rem", data=msleep)plt.show()
Añadir una línea de tendencia
import seaborn as sns sns.lmplot(x="sleep_total", y="sleep_rem", data=msleep, ci=None)plt.show()
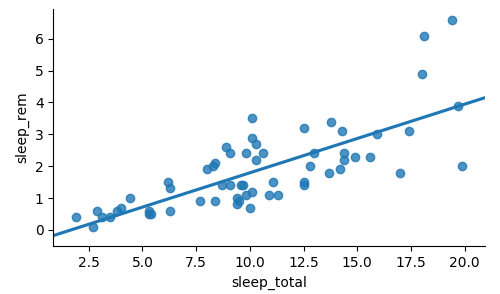
Calcular correlación
msleep['sleep_total'].corr(msleep['sleep_rem'])
0.751755
msleep['sleep_rem'].corr(msleep['sleep_total'])
0.751755
Muchas formas de calcular la correlación
- Utilizada en este curso: correlación producto-momento de Pearson ($r$)
- Más frecuentes
- $\bar{x} =$ media de $x$
- $\sigma_x =$ desviación típica de $x$
$$ r = \frac{1}{n - 1} \sum_{i=1}^{n} \frac{(x_i - \bar{x})(y_i - \bar{y})}{\sigma_x \cdot \sigma_y}$$
- Variaciones de esta fórmula:
- Tau de Kendall
- Rho de Spearman
¡Vamos a practicar!
Introducción a la estadística en Python

